九年级数学(浙教版)上册复习课件第3章-圆的基本性质 (共19张PPT)
文档属性
| 名称 | 九年级数学(浙教版)上册复习课件第3章-圆的基本性质 (共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-11 15:41:48 | ||
图片预览




文档简介
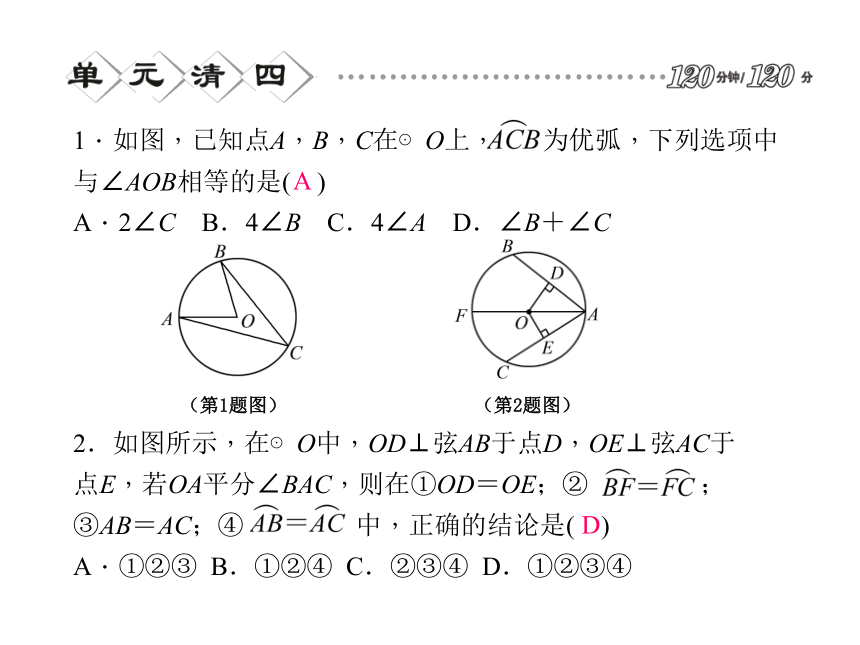
课件19张PPT。第3章 圆的基本性质1.如图,已知点A,B,C在⊙O上, 为优弧,下列选项中与∠AOB相等的是( )
A.2∠C B.4∠B C.4∠A D.∠B+∠C2.如图所示,在⊙O中,OD⊥弦AB于点D,OE⊥弦AC于点E,若OA平分∠BAC,则在①OD=OE;② ;③AB=AC;④ 中,正确的结论是( )
A.①②③ B.①②④ C.②③④ D.①②③④ AD(第1题图) (第2题图) 3.如图,点A,B,C,D,O都在方格纸的格点上,若△COD是由△AOB绕点O按逆时针方向旋转而得,则旋转的角度为( )
A.30° B.45° C.90° D.135°4.点A的坐标为(1,3),⊙A的半径为5,则点B(-3,0)与⊙A的位置关系是( )
A.点B在⊙A外 B.点B在⊙A上
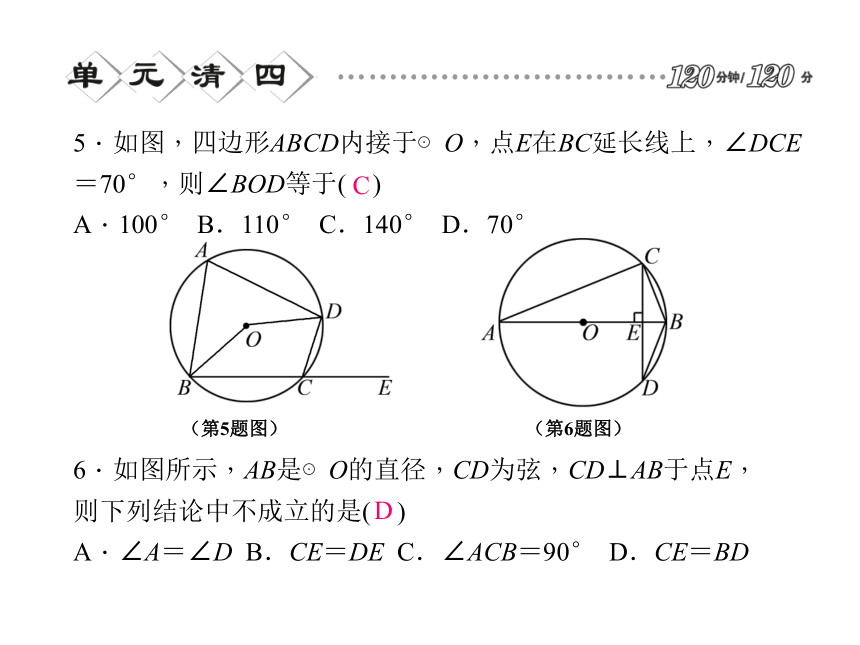
C.点B在⊙A内 D.不能确定CB5.如图,四边形ABCD内接于⊙O,点E在BC延长线上,∠DCE=70°,则∠BOD等于( )
A.100° B.110° C.140° D.70°6.如图所示,AB是⊙O的直径,CD为弦,CD⊥AB于点E,则下列结论中不成立的是( )
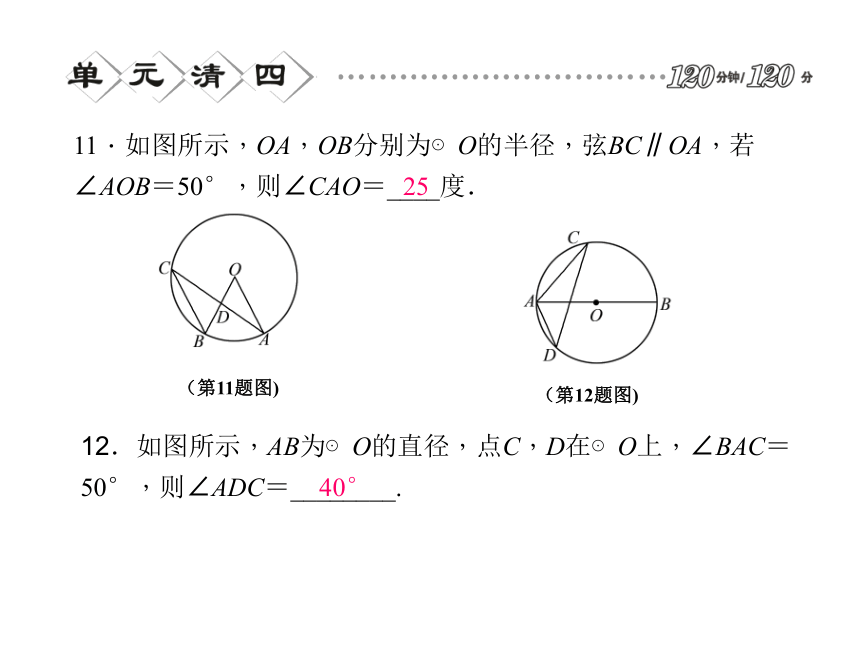
A.∠A=∠D B.CE=DE C.∠ACB=90° D.CE=BD(第6题图) (第5题图) CD7.如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于( )8.⊙O是等边△ABC的外接圆,⊙O的半径为2,则等边△ABC的边长为( )DC9.在Rt△ABC中,斜边AB=4,∠B=60°,将△ABC绕点B按顺时针方向旋转60°,顶点C运动的路线长是( )10.如图所示,以BC为直径,在半径为2、圆心角为90°的扇形内作半圆,交弦AB于点D,连结CD,则图中阴影部分的面积是( )BA11.如图所示,OA,OB分别为⊙O的半径,弦BC∥OA,若∠AOB=50°,则∠CAO=____度.12.如图所示,AB为⊙O的直径,点C,D在⊙O上,∠BAC=50°,则∠ADC=________.(第11题图) (第12题图) 2540° 13.如图所示,当半径为30 cm的转轮转过120°角时,传送带上的物体A平移的距离为_______cm.14.如图,在⊙O中,圆心角∠AOB=120°,弦AB=2cm,则OA=____cm.(第13题图)(第14题图)20π215.如图,已知正方形ABCD的边长为12 cm,E为CD边上一点,DE=5 cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为_______cm.16.如图,Rt△ABC中,∠C=90°,AC=2,BC=4,分别以AC,BC为直径作半圆,则图中阴影部分的面积为___________.(第15题图)(第16题图)17.(6分)已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D.(如图所示)
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长.解:(1)证明:过点O作OE⊥AB于点E,则CE=DE,AE=BE.∴AE-CE=BE-DE,即AC=BD 18.(8分)图①为杭州国际会议中心,是全国最大的球形建筑,如图②是球体的轴截面示意图,已知这个球体的高度为86米,球的半径为50米,则这个国际会议中心建筑的占地面积为多少?(结果保留π)解:连结OA,∵OA2=AD2+OD2,∴AD2=OA2-OD2=502-(86-50)2=1 204,∴S=π·AD2=1 204π(平方米).答:这个国际会议中心建筑的占地面积为1 204π平方米19.(8分)如图,在⊙O中,C为 的中点,连结AC并延长至点D,使CD=CA,连结DB并延长DB交⊙O于点E,连结AE.
(1)求证:AE是⊙O的直径;
(2)求证:AE=DE.证明:(1)连结CB,AB,CE,∵点C为劣弧AB上的中点,∴CB=CA,又∵CD=CA,∴AC=CD=BC,∴∠ABC=∠BAC,∠DBC=∠D,∴∠ABD=90°,∴∠ABE=90°,
∴AE是⊙O的直径 (2)∵AE是⊙O的直径,∴∠ACE=90°,即EC⊥AD,∵AC=CD,∴AE=DE20.(8分)已知⊙O中,弦AB⊥弦CD于点E,求证:∠AOD+∠BOC=180°.证明:连结AC,BD,由圆周角定理得:∠AOD=2∠ABD,∠BOC=2∠CDB,∠CAB=∠CDB,∵弦AB⊥弦CD,∴∠ABD+∠BDC=90°,∴∠AOD+∠BOC=2∠ABD+2∠CDB=2(∠ABD+∠CDB)=2×90°=180°21.(8分)如图,AB是⊙O的直径,C,D是⊙O上的两点,且AC=CD.
(1)求证:OC∥BD;
(2)若BC将四边形OBDC分成面积相等的两个三角形,试确定四边形OBDC的形状.22.(8分)圆心角都是90°的扇形AOB与扇形COD如图所示那样叠放在一起,连结AC,BD.
(1)求证:△AOC≌△BOD;
(2)若AO=3 cm,OC=1 cm,求阴影部分的面积.解:(1)证明:∵∠COD=∠AOB=90°,∴∠AOC=∠BOD.又∵OA=OB,OC=OD,∴△AOC≌△BOD23.(8分)如图,在锐角△ABC中,AC是最短边,以AC的中点O为圆心,AC为直径作⊙O,交BC于点E,过O作OD∥BC交⊙O于点D,连结AE,AD,DC.求证:
(1)D是 的中点;
(2)∠DAO=∠B+∠BAD.证明:(1)∵AC是⊙O的直径,∴AE⊥BC.∵OD∥BC,∴OD⊥AE,∴D是 的中点 (2)∵AE⊥BC,∴∠B+∠BAD+∠DAE=90°.∵D是 的中点,∴ ,∴∠ACD=∠DAE.∵AC是⊙O的直径,∴∠DAO+∠ACD=90°.∵∠B+∠BAD+∠DAE=90°,∠ACD=∠DAE,∠DAO+∠ACD=90°,∴∠DAO=∠B+∠BAD24.(12分)如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC,AC于点D,E,且点D为BC的中点.
(1)求证:△ABC为等边三角形;
(2)求DE的长;
(3)在线段AB的延长线上是否存在一点P,使△PBD≌△AED?若存在,请求出PB的长;若不存在,请说明理由.解:(1)证明:如图,连结AD,∵AB是⊙O的直径,∴∠ADB=90°,即AD⊥BC.∵点D是BC的中点,∴AD是线段BC的垂直平分线,∴AB=AC.∵AB=BC,∴AB=BC=AC,∴△ABC为等边三角形
A.2∠C B.4∠B C.4∠A D.∠B+∠C2.如图所示,在⊙O中,OD⊥弦AB于点D,OE⊥弦AC于点E,若OA平分∠BAC,则在①OD=OE;② ;③AB=AC;④ 中,正确的结论是( )
A.①②③ B.①②④ C.②③④ D.①②③④ AD(第1题图) (第2题图) 3.如图,点A,B,C,D,O都在方格纸的格点上,若△COD是由△AOB绕点O按逆时针方向旋转而得,则旋转的角度为( )
A.30° B.45° C.90° D.135°4.点A的坐标为(1,3),⊙A的半径为5,则点B(-3,0)与⊙A的位置关系是( )
A.点B在⊙A外 B.点B在⊙A上
C.点B在⊙A内 D.不能确定CB5.如图,四边形ABCD内接于⊙O,点E在BC延长线上,∠DCE=70°,则∠BOD等于( )
A.100° B.110° C.140° D.70°6.如图所示,AB是⊙O的直径,CD为弦,CD⊥AB于点E,则下列结论中不成立的是( )
A.∠A=∠D B.CE=DE C.∠ACB=90° D.CE=BD(第6题图) (第5题图) CD7.如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于( )8.⊙O是等边△ABC的外接圆,⊙O的半径为2,则等边△ABC的边长为( )DC9.在Rt△ABC中,斜边AB=4,∠B=60°,将△ABC绕点B按顺时针方向旋转60°,顶点C运动的路线长是( )10.如图所示,以BC为直径,在半径为2、圆心角为90°的扇形内作半圆,交弦AB于点D,连结CD,则图中阴影部分的面积是( )BA11.如图所示,OA,OB分别为⊙O的半径,弦BC∥OA,若∠AOB=50°,则∠CAO=____度.12.如图所示,AB为⊙O的直径,点C,D在⊙O上,∠BAC=50°,则∠ADC=________.(第11题图) (第12题图) 2540° 13.如图所示,当半径为30 cm的转轮转过120°角时,传送带上的物体A平移的距离为_______cm.14.如图,在⊙O中,圆心角∠AOB=120°,弦AB=2cm,则OA=____cm.(第13题图)(第14题图)20π215.如图,已知正方形ABCD的边长为12 cm,E为CD边上一点,DE=5 cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为_______cm.16.如图,Rt△ABC中,∠C=90°,AC=2,BC=4,分别以AC,BC为直径作半圆,则图中阴影部分的面积为___________.(第15题图)(第16题图)17.(6分)已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D.(如图所示)
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长.解:(1)证明:过点O作OE⊥AB于点E,则CE=DE,AE=BE.∴AE-CE=BE-DE,即AC=BD 18.(8分)图①为杭州国际会议中心,是全国最大的球形建筑,如图②是球体的轴截面示意图,已知这个球体的高度为86米,球的半径为50米,则这个国际会议中心建筑的占地面积为多少?(结果保留π)解:连结OA,∵OA2=AD2+OD2,∴AD2=OA2-OD2=502-(86-50)2=1 204,∴S=π·AD2=1 204π(平方米).答:这个国际会议中心建筑的占地面积为1 204π平方米19.(8分)如图,在⊙O中,C为 的中点,连结AC并延长至点D,使CD=CA,连结DB并延长DB交⊙O于点E,连结AE.
(1)求证:AE是⊙O的直径;
(2)求证:AE=DE.证明:(1)连结CB,AB,CE,∵点C为劣弧AB上的中点,∴CB=CA,又∵CD=CA,∴AC=CD=BC,∴∠ABC=∠BAC,∠DBC=∠D,∴∠ABD=90°,∴∠ABE=90°,
∴AE是⊙O的直径 (2)∵AE是⊙O的直径,∴∠ACE=90°,即EC⊥AD,∵AC=CD,∴AE=DE20.(8分)已知⊙O中,弦AB⊥弦CD于点E,求证:∠AOD+∠BOC=180°.证明:连结AC,BD,由圆周角定理得:∠AOD=2∠ABD,∠BOC=2∠CDB,∠CAB=∠CDB,∵弦AB⊥弦CD,∴∠ABD+∠BDC=90°,∴∠AOD+∠BOC=2∠ABD+2∠CDB=2(∠ABD+∠CDB)=2×90°=180°21.(8分)如图,AB是⊙O的直径,C,D是⊙O上的两点,且AC=CD.
(1)求证:OC∥BD;
(2)若BC将四边形OBDC分成面积相等的两个三角形,试确定四边形OBDC的形状.22.(8分)圆心角都是90°的扇形AOB与扇形COD如图所示那样叠放在一起,连结AC,BD.
(1)求证:△AOC≌△BOD;
(2)若AO=3 cm,OC=1 cm,求阴影部分的面积.解:(1)证明:∵∠COD=∠AOB=90°,∴∠AOC=∠BOD.又∵OA=OB,OC=OD,∴△AOC≌△BOD23.(8分)如图,在锐角△ABC中,AC是最短边,以AC的中点O为圆心,AC为直径作⊙O,交BC于点E,过O作OD∥BC交⊙O于点D,连结AE,AD,DC.求证:
(1)D是 的中点;
(2)∠DAO=∠B+∠BAD.证明:(1)∵AC是⊙O的直径,∴AE⊥BC.∵OD∥BC,∴OD⊥AE,∴D是 的中点 (2)∵AE⊥BC,∴∠B+∠BAD+∠DAE=90°.∵D是 的中点,∴ ,∴∠ACD=∠DAE.∵AC是⊙O的直径,∴∠DAO+∠ACD=90°.∵∠B+∠BAD+∠DAE=90°,∠ACD=∠DAE,∠DAO+∠ACD=90°,∴∠DAO=∠B+∠BAD24.(12分)如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC,AC于点D,E,且点D为BC的中点.
(1)求证:△ABC为等边三角形;
(2)求DE的长;
(3)在线段AB的延长线上是否存在一点P,使△PBD≌△AED?若存在,请求出PB的长;若不存在,请说明理由.解:(1)证明:如图,连结AD,∵AB是⊙O的直径,∴∠ADB=90°,即AD⊥BC.∵点D是BC的中点,∴AD是线段BC的垂直平分线,∴AB=AC.∵AB=BC,∴AB=BC=AC,∴△ABC为等边三角形
同课章节目录
