八年级数学上册2.4等腰三角形的判定定理同步练习(含答案)
文档属性
| 名称 | 八年级数学上册2.4等腰三角形的判定定理同步练习(含答案) | 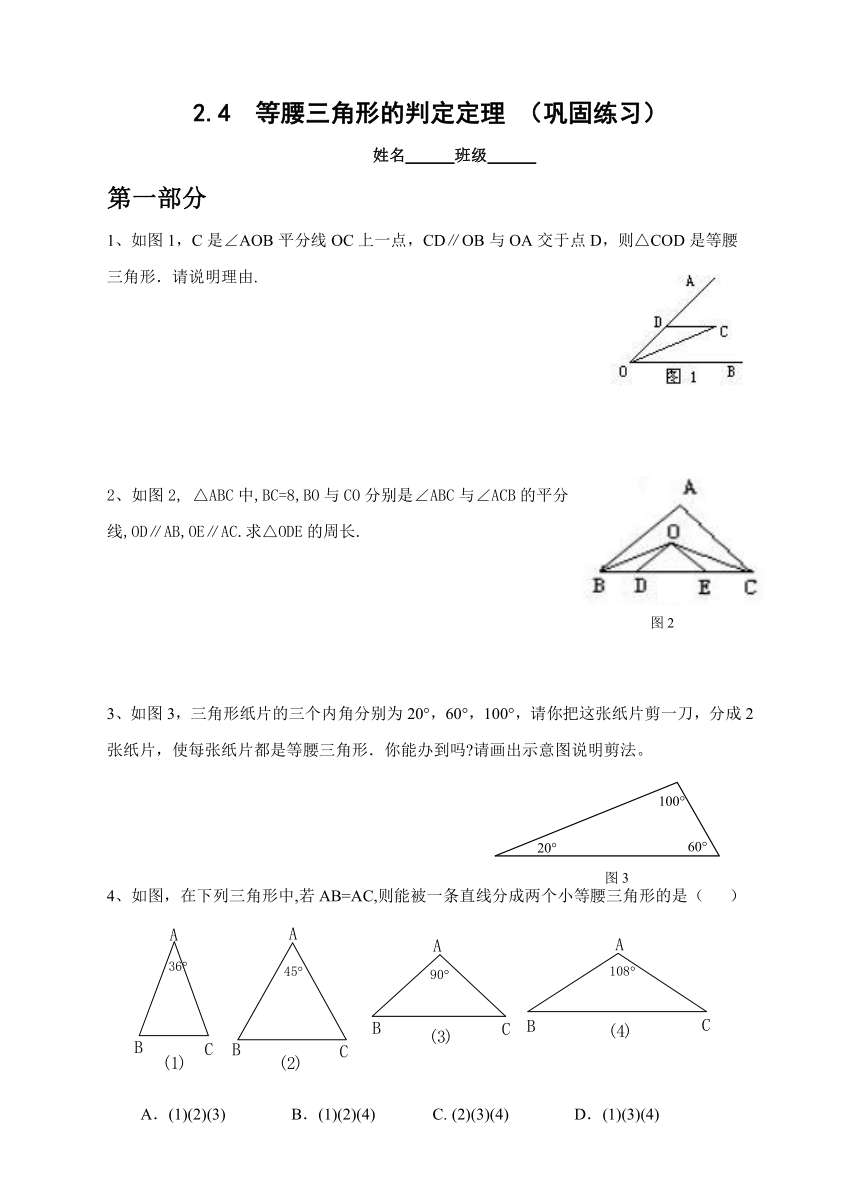 | |
| 格式 | zip | ||
| 文件大小 | 69.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-17 07:33:59 | ||
图片预览



文档简介
2.4
等腰三角形的判定定理
(巩固练习)
姓名
班级
第一部分
1、如图1,C是∠AOB平分线OC上一点,CD∥OB与OA交于点D,则△COD是等腰三角形.请说明理由.
2、如图2,
△ABC中,BC=8,BO与CO分别是∠ABC与∠ACB的平分线,OD∥AB,OE∥AC.求△ODE的周长.
3、如图3,三角形纸片的三个内角分别为20°,60°,100°,请你把这张纸片剪一刀,分成2张纸片,使每张纸片都是等腰三角形.你能办到吗 请画出示意图说明剪法。
4、如图,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是(
)
A.(1)(2)(3)
B.(1)(2)(4)
C.
(2)(3)(4)
D.(1)(3)(4)
第二部分
1.
等腰△ABC中,顶角∠A=40°,则一个底角∠B=
度.
2.在△ABC中,若∠A=∠C,则
=
.
3.
在△ABC中,已知∠A=65°,∠C=50°,则△ABC是
三角形.
4.如果一个三角形有两个外角相等,那么这个三角形是
三角形.
5.如图7,上午8时,一条船从A处出发,以15海里/时的速度向正北航行,10时到达B处,从A、B望灯塔C,测得∠NAC=42°,∠NBC=84°,则从B处到灯塔C的距离_______.
6.若三角形一个外角的平分线平行于第三边,则这个三角形一定是
三角形.
7.如图8,BD与CE交于点A,AB=AC,DE∥BC.则△ADE是等腰三角形,请说明理由.
8.
如图9,把一张对边平行的纸条如图折叠,则重合部分必是等腰三角形.请说明理由.
9.
如图10, ABC中,D、E分别是AC、AB上的点,BD与CE交于点O.
给出下列四个条件:①∠EBD=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
(1)
上述四个条件中,哪两个条件可判定△ABC是等腰三角形(用序号写出所有情形);
(2)
选择第(1)小题中的一种情形,试说明△ABC是等腰三角形.
参考答案
第一部分
4、如图,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是(
)
A.(1)(2)(3)
B.(1)(2)(4)
C.
(2)(3)(4)
D.(1)(3)(4)
答案:D
第二部分
1.
等腰△ABC中,顶角∠A=40°,则一个底角∠B=
度.
答案:70°
2.在△ABC中,若∠A=∠C,则
=
.
答案:AB=BC
3.
在△ABC中,已知∠A=65°,∠C=50°,则△ABC是
三角形.
答案:等腰
4.如果一个三角形有两个外角相等,那么这个三角形是
三角形.
答案:等腰
5.如图7,上午8时,一条船从A处出发,以15海里/时的速度向正北航行,10时到达B处,从A、B望灯塔C,测得∠NAC=42°,∠NBC=84°,则从B处到灯塔C的距离_______.
答案:30海里
6.若三角形一个外角的平分线平行于第三边,则这个三角形一定是
三角形.
答案:等腰三角形
7.如图8,BD与CE交于点A,AB=AC,DE∥BC.则△ADE是等腰三角形,请说明理由.
解:∵AB=AC,
∴∠B=∠C.
∵DE∥BC,
∴∠D=∠B,
∠E=∠C.
∴∠D=∠E,
∴△ADE是等腰三角形.
8.
如图9,把一张对边平行的纸条如图折叠,则重合部分必是等腰三角形.请说明理由.
解:由题意,
得∠EAC=∠BAC.
∵DC∥AB,
∴∠ECA=∠BAC.
∴∠EAC=∠ECA,
即△EAC是等腰三角形.
9.
如图10, ABC中,D、E分别是AC、AB上的点,BD与CE交于点O.
给出下列四个条件:①∠EBD=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
(1)
上述四个条件中,哪两个条件可判定△ABC是等腰三角形(用序号写出所有情形);
(2)
选择第(1)小题中的一种情形,试说明△ABC是等腰三角形.
解:(1)
①③或①④或②③或②④.
(2)
如②④.
∵OB=OC,
∴∠OCB=∠OBC.
又∠BEO=∠CDO,
BC=CB.
∴△EBC≌△DCB,
∴∠EBC=∠DCB,
∴△ABC是等腰三角形.
图2
图3
图7
图8
图9
图10
图7
图8
图9
图10
等腰三角形的判定定理
(巩固练习)
姓名
班级
第一部分
1、如图1,C是∠AOB平分线OC上一点,CD∥OB与OA交于点D,则△COD是等腰三角形.请说明理由.
2、如图2,
△ABC中,BC=8,BO与CO分别是∠ABC与∠ACB的平分线,OD∥AB,OE∥AC.求△ODE的周长.
3、如图3,三角形纸片的三个内角分别为20°,60°,100°,请你把这张纸片剪一刀,分成2张纸片,使每张纸片都是等腰三角形.你能办到吗 请画出示意图说明剪法。
4、如图,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是(
)
A.(1)(2)(3)
B.(1)(2)(4)
C.
(2)(3)(4)
D.(1)(3)(4)
第二部分
1.
等腰△ABC中,顶角∠A=40°,则一个底角∠B=
度.
2.在△ABC中,若∠A=∠C,则
=
.
3.
在△ABC中,已知∠A=65°,∠C=50°,则△ABC是
三角形.
4.如果一个三角形有两个外角相等,那么这个三角形是
三角形.
5.如图7,上午8时,一条船从A处出发,以15海里/时的速度向正北航行,10时到达B处,从A、B望灯塔C,测得∠NAC=42°,∠NBC=84°,则从B处到灯塔C的距离_______.
6.若三角形一个外角的平分线平行于第三边,则这个三角形一定是
三角形.
7.如图8,BD与CE交于点A,AB=AC,DE∥BC.则△ADE是等腰三角形,请说明理由.
8.
如图9,把一张对边平行的纸条如图折叠,则重合部分必是等腰三角形.请说明理由.
9.
如图10, ABC中,D、E分别是AC、AB上的点,BD与CE交于点O.
给出下列四个条件:①∠EBD=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
(1)
上述四个条件中,哪两个条件可判定△ABC是等腰三角形(用序号写出所有情形);
(2)
选择第(1)小题中的一种情形,试说明△ABC是等腰三角形.
参考答案
第一部分
4、如图,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的是(
)
A.(1)(2)(3)
B.(1)(2)(4)
C.
(2)(3)(4)
D.(1)(3)(4)
答案:D
第二部分
1.
等腰△ABC中,顶角∠A=40°,则一个底角∠B=
度.
答案:70°
2.在△ABC中,若∠A=∠C,则
=
.
答案:AB=BC
3.
在△ABC中,已知∠A=65°,∠C=50°,则△ABC是
三角形.
答案:等腰
4.如果一个三角形有两个外角相等,那么这个三角形是
三角形.
答案:等腰
5.如图7,上午8时,一条船从A处出发,以15海里/时的速度向正北航行,10时到达B处,从A、B望灯塔C,测得∠NAC=42°,∠NBC=84°,则从B处到灯塔C的距离_______.
答案:30海里
6.若三角形一个外角的平分线平行于第三边,则这个三角形一定是
三角形.
答案:等腰三角形
7.如图8,BD与CE交于点A,AB=AC,DE∥BC.则△ADE是等腰三角形,请说明理由.
解:∵AB=AC,
∴∠B=∠C.
∵DE∥BC,
∴∠D=∠B,
∠E=∠C.
∴∠D=∠E,
∴△ADE是等腰三角形.
8.
如图9,把一张对边平行的纸条如图折叠,则重合部分必是等腰三角形.请说明理由.
解:由题意,
得∠EAC=∠BAC.
∵DC∥AB,
∴∠ECA=∠BAC.
∴∠EAC=∠ECA,
即△EAC是等腰三角形.
9.
如图10, ABC中,D、E分别是AC、AB上的点,BD与CE交于点O.
给出下列四个条件:①∠EBD=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
(1)
上述四个条件中,哪两个条件可判定△ABC是等腰三角形(用序号写出所有情形);
(2)
选择第(1)小题中的一种情形,试说明△ABC是等腰三角形.
解:(1)
①③或①④或②③或②④.
(2)
如②④.
∵OB=OC,
∴∠OCB=∠OBC.
又∠BEO=∠CDO,
BC=CB.
∴△EBC≌△DCB,
∴∠EBC=∠DCB,
∴△ABC是等腰三角形.
图2
图3
图7
图8
图9
图10
图7
图8
图9
图10
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
