浙教版九年级数学上《1.3二次函数的性质》巩固练习含答案
文档属性
| 名称 | 浙教版九年级数学上《1.3二次函数的性质》巩固练习含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 190.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-29 07:23:43 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
1.3
二次函数的性质
(巩固练习)
姓名
班级
第一部分(难度有层次性,对于班级上中下同学都能照顾到!)
1.
二次函数的图象向右平移3个单位,得到新的图象的函数表达式是……(
)
A.
B.
C.
D.
2.
抛物线y=3(x-1)+1的顶点坐标是…………………………………………………(
)
A.(1,1)
B.(-1,1)
C.(-1,-1)
D.(1,-1)
3.
二次函数的最小值是……………………………………………(
)
A.
2
B.
-2
C.
1
D.
-1
4.已知二次函数的最大值为0,则…………(
)
A.
B.
C.
D.
5.
已知某二次函数的图象如图所示,则这个二次函数的解析式为(
)
A.
B.
C.
D.
第二部分
1.
二次函数y=x2-2x+2的顶点坐标是
,对称轴是
.
2.
二次函数的最
值是
.
3.
函数y=x2-4x-5与x轴的交点坐标是_______________,与y轴的交点坐标是
.
4.
抛物线y=(x+2)2-1的图象开口向
,当x
时,y随x的增大而增大.
5、对于二次函数y=-2x2+8x-8,通过配方变形.
(1)
说出的图象的开口方向、对称轴、
顶点坐标,这个函数有最大值还是最小值 这个值是多少
(2)
求出此抛物线与x,y轴的交点坐标;
(3)
结合图象回答:当x为何值时,y随着x的增大而减小.
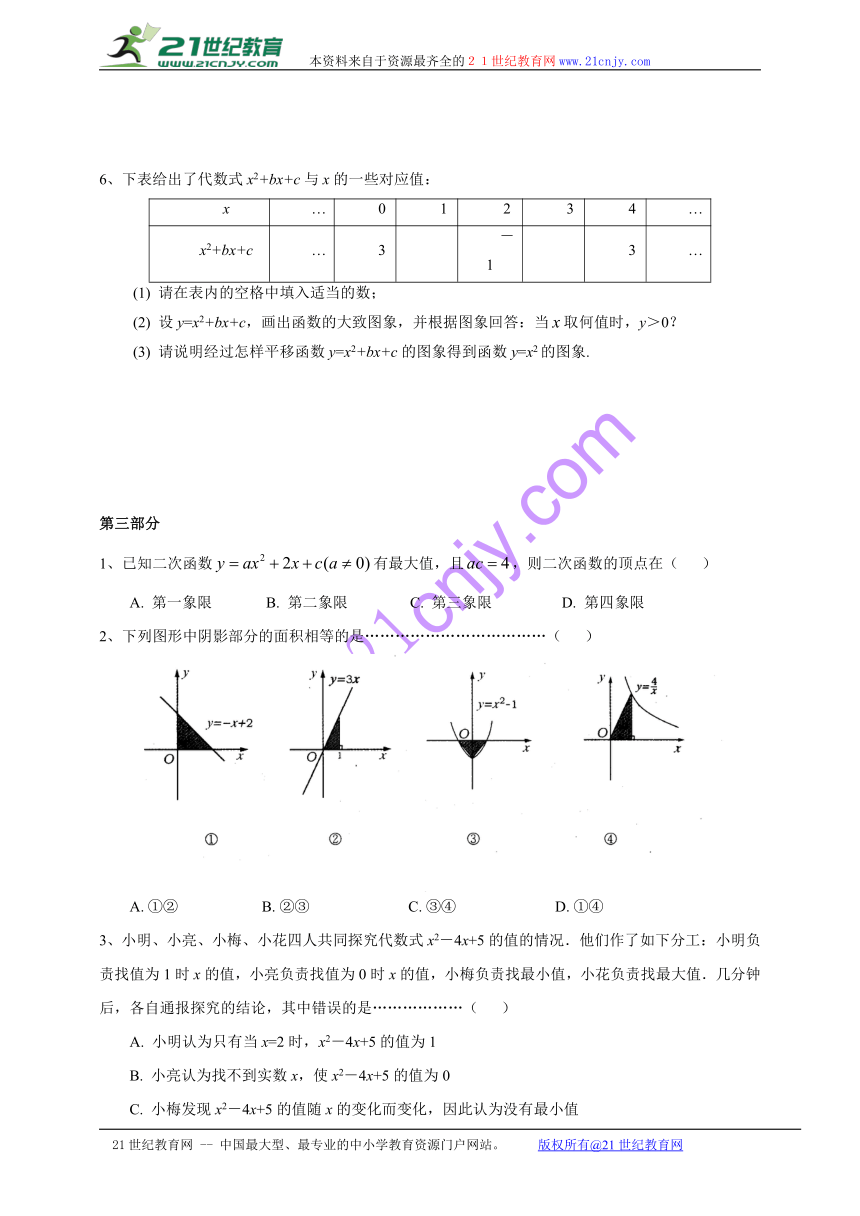
6、下表给出了代数式x2+bx+c与x的一些对应值:
x
…
0
1
2
3
4
…
x2+bx+c
…
3
-1
3
…
(1)
请在表内的空格中填入适当的数;
(2)
设y=x2+bx+c,画出函数的大致图象,并根据图象回答:当取何值时,y>0?
(3)
请说明经过怎样平移函数y=x2+bx+c的图象得到函数y=x2的图象.
第三部分
1、已知二次函数有最大值,且,则二次函数的顶点在(
)
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
2、下列图形中阴影部分的面积相等的是………………………………(
)
A.
①②
B.
②③
C.
③④
D.
①④21世纪教育网版权所有
3、小明、小亮、小梅、小花四人共同探究代
( http: / / www.21cnjy.com )数式x2-4x+5的值的情况.他们作了如下分工:小明负责找值为1时x的值,小亮负责找值为0时x的值,小梅负责找最小值,小花负责找最大值.几分钟后,各自通报探究的结论,其中错误的是………………(
)21教育网
A.
小明认为只有当x=2时,x2-4x+5的值为1
B.
小亮认为找不到实数x,使x2-4x+5的值为0
C.
小梅发现x2-4x+5的值随x的变化而变化,因此认为没有最小值
D.
小花发现当x取大于2的实数时,x2-4x+5的值随x的增大而增大,因此认为没有最大值.
参考答案
第一部分
1.
答案:D
2.
答案:A
3.
答案:A
4.答案:D
5.
答案:D
第二部分
1.
答案:(1,1)
直线x=1
2.
答案:三
3.答案:(-1,0),(5,0)
(0,-5)
4.
答案:上
≥-2
5、(1)
∵a=-2<0,b=8,c=-8,∴=2,=0.
∴抛物线的开口向下,对称轴为直线x=2,顶点(2,0),函数最大值为0.
(2)
当y=0时,-2x2+8x-8=0,解得x=0,即抛物线与x轴的交点坐标是(2,0);
当x=0时,y=-8,即抛物线与y轴的交点坐标是(0,-8).
(3)
∵a<0,∴当x≥2时,y随着x的增大而减小.
6、(1)
∵把(0,3)和(2,-1)分别代入代数式x2+bx+c,得
,解得,即代数式为x2-4x+3.
∴把x=1,3分别代入,得代数式为x2-4x+3的值均为0.
(2)
y=x2-4x+3=(x-2)2-1,∴顶点(2,-1),对称轴为直线x=2.
又抛物线与x轴交点坐标是(1,0)和(3,0),与y轴的交点
坐标是(0,3).
函数的大致图象如图.
由图象得,当x<1或x>3时y>0.
(3)
把抛物线y=x2的图象向右平移2个单位,再向下平移
1个单位可得y=x2-4x+3的图象.
第三部分
1、解析:∵抛物线有最大值,∴a<0,∴=>0,=<0.
答案:D
2、解析:①中直线与2与轴交点为(2,0),(0,2),∴S阴影=×2×2=2;②中x=1时,y=3,∴S阴影=×1×3=;③中抛物线与坐标轴的交点坐标为(-1,0),(1,0),(0,-1),∴S阴影=×2×1=1;④中S阴影=|xy|=2.
答案:D
3、答案:C
21世纪教育网
--
中国最大型、最专业的中小学教育资源门户网站。
版权所有@21世纪教育网
1.3
二次函数的性质
(巩固练习)
姓名
班级
第一部分(难度有层次性,对于班级上中下同学都能照顾到!)
1.
二次函数的图象向右平移3个单位,得到新的图象的函数表达式是……(
)
A.
B.
C.
D.
2.
抛物线y=3(x-1)+1的顶点坐标是…………………………………………………(
)
A.(1,1)
B.(-1,1)
C.(-1,-1)
D.(1,-1)
3.
二次函数的最小值是……………………………………………(
)
A.
2
B.
-2
C.
1
D.
-1
4.已知二次函数的最大值为0,则…………(
)
A.
B.
C.
D.
5.
已知某二次函数的图象如图所示,则这个二次函数的解析式为(
)
A.
B.
C.
D.
第二部分
1.
二次函数y=x2-2x+2的顶点坐标是
,对称轴是
.
2.
二次函数的最
值是
.
3.
函数y=x2-4x-5与x轴的交点坐标是_______________,与y轴的交点坐标是
.
4.
抛物线y=(x+2)2-1的图象开口向
,当x
时,y随x的增大而增大.
5、对于二次函数y=-2x2+8x-8,通过配方变形.
(1)
说出的图象的开口方向、对称轴、
顶点坐标,这个函数有最大值还是最小值 这个值是多少
(2)
求出此抛物线与x,y轴的交点坐标;
(3)
结合图象回答:当x为何值时,y随着x的增大而减小.
6、下表给出了代数式x2+bx+c与x的一些对应值:
x
…
0
1
2
3
4
…
x2+bx+c
…
3
-1
3
…
(1)
请在表内的空格中填入适当的数;
(2)
设y=x2+bx+c,画出函数的大致图象,并根据图象回答:当取何值时,y>0?
(3)
请说明经过怎样平移函数y=x2+bx+c的图象得到函数y=x2的图象.
第三部分
1、已知二次函数有最大值,且,则二次函数的顶点在(
)
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
2、下列图形中阴影部分的面积相等的是………………………………(
)
A.
①②
B.
②③
C.
③④
D.
①④21世纪教育网版权所有
3、小明、小亮、小梅、小花四人共同探究代
( http: / / www.21cnjy.com )数式x2-4x+5的值的情况.他们作了如下分工:小明负责找值为1时x的值,小亮负责找值为0时x的值,小梅负责找最小值,小花负责找最大值.几分钟后,各自通报探究的结论,其中错误的是………………(
)21教育网
A.
小明认为只有当x=2时,x2-4x+5的值为1
B.
小亮认为找不到实数x,使x2-4x+5的值为0
C.
小梅发现x2-4x+5的值随x的变化而变化,因此认为没有最小值
D.
小花发现当x取大于2的实数时,x2-4x+5的值随x的增大而增大,因此认为没有最大值.
参考答案
第一部分
1.
答案:D
2.
答案:A
3.
答案:A
4.答案:D
5.
答案:D
第二部分
1.
答案:(1,1)
直线x=1
2.
答案:三
3.答案:(-1,0),(5,0)
(0,-5)
4.
答案:上
≥-2
5、(1)
∵a=-2<0,b=8,c=-8,∴=2,=0.
∴抛物线的开口向下,对称轴为直线x=2,顶点(2,0),函数最大值为0.
(2)
当y=0时,-2x2+8x-8=0,解得x=0,即抛物线与x轴的交点坐标是(2,0);
当x=0时,y=-8,即抛物线与y轴的交点坐标是(0,-8).
(3)
∵a<0,∴当x≥2时,y随着x的增大而减小.
6、(1)
∵把(0,3)和(2,-1)分别代入代数式x2+bx+c,得
,解得,即代数式为x2-4x+3.
∴把x=1,3分别代入,得代数式为x2-4x+3的值均为0.
(2)
y=x2-4x+3=(x-2)2-1,∴顶点(2,-1),对称轴为直线x=2.
又抛物线与x轴交点坐标是(1,0)和(3,0),与y轴的交点
坐标是(0,3).
函数的大致图象如图.
由图象得,当x<1或x>3时y>0.
(3)
把抛物线y=x2的图象向右平移2个单位,再向下平移
1个单位可得y=x2-4x+3的图象.
第三部分
1、解析:∵抛物线有最大值,∴a<0,∴=>0,=<0.
答案:D
2、解析:①中直线与2与轴交点为(2,0),(0,2),∴S阴影=×2×2=2;②中x=1时,y=3,∴S阴影=×1×3=;③中抛物线与坐标轴的交点坐标为(-1,0),(1,0),(0,-1),∴S阴影=×2×1=1;④中S阴影=|xy|=2.
答案:D
3、答案:C
21世纪教育网
--
中国最大型、最专业的中小学教育资源门户网站。
版权所有@21世纪教育网
同课章节目录
