第5章特殊的平行四边形练习A卷

浙教新版八年级下第5章特殊的平行四边形练习A卷
学校：___________姓名：___________班级：___________考号：___________
一、 选择题
1. 依次连结菱形四条边的中点所构成的四边形是 ( ?? )
A．菱形 B．矩形 C．一般平行四边形 D．一般四边形
2. 若菱形ABCD的周长为8，对角线AC=2，则∠ABC的度数是( ?? )
A．120° B．60° C．30° D．150°
3. 下列命题中,正确的是( )
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是平行四边形
C.对角线互相垂直的四边形是菱形
D.对角线互相垂直且相等的四边形是正方形
4. 已知四边形的对角线互相垂直，则顺次连接该四边形各边中点所得的四边形是 ( ) A．梯形 B．矩形 C．菱形 D．正方形 2·1·c·n·j·y
5. 正方形具有而一般菱形不具有的性质是( )
A．四条边都相等 B．对角线互相垂直平分 C．对角线相等 D．每一条对角线平分一组对角
6. 下列说法中的错误的是( )．
A．一组邻边相等的矩形是正方形
B．一组邻边相等的平行四边形是菱形
C．一组对边相等且有一个角是直角的四边形是矩形
D．一组对边平行且相等的四边形是平行四边形
7. 如图，在菱形ABCD中，对角线AC=4，∠BAD=120°，则菱形ABCD的周长为 ( )【出处：21教育名师】
A．15 B．16 C．18 D．20
8. 如图是用4个相同的小矩形与1个小正方形密铺而成的正方形图案，已知该图案的面积为 ，小正方形的面积为4，若用 表示小矩形的两边长，请观察图案，指出以下关系式中不正确的是 21教育名师原创作品
A． B． C． D．
9. 在菱形ABCD中，若∠ADC=120°，对角线AC=6，则菱形的周长是( )
A．4 B．24 C．8 D．24
10. 如图,矩形纸片ABCD中,AD=9,AB=3,将其折叠,使点D与点B重合,折痕为EF,那么折痕EF的长为（ ） 21*cnjy*com
A.8 B.6 C. D.3
11. 如图是一瓷砖的图案，用这种瓷砖铺设地面，图（2）铺成了一个2×2的近似正方形，其中完整菱形共有5个；若铺成3×3的近似正方形图案（3），其中完整的菱形有13个；铺成4×4的近似正方形图案（4），其中完整的菱形有25个；如此下去可铺成一个 n × n 的近似正方形图案．当得到完整的菱形共181个时， n 的值为（ ）
A．7 ? ?B． 8 C ．9 ? ?D．10
二、 填空题
12. 若菱形的周长为16cm，则此菱形的边长是______cm．
13. 正方形既是特殊的________，又是特殊的_________，所以它同时具有______和________的性质：正方形的四个角_______，四条边________；正方形的对角线_____，并且_________，每条对角线平分_________． 【来源：21·世纪·教育·网】
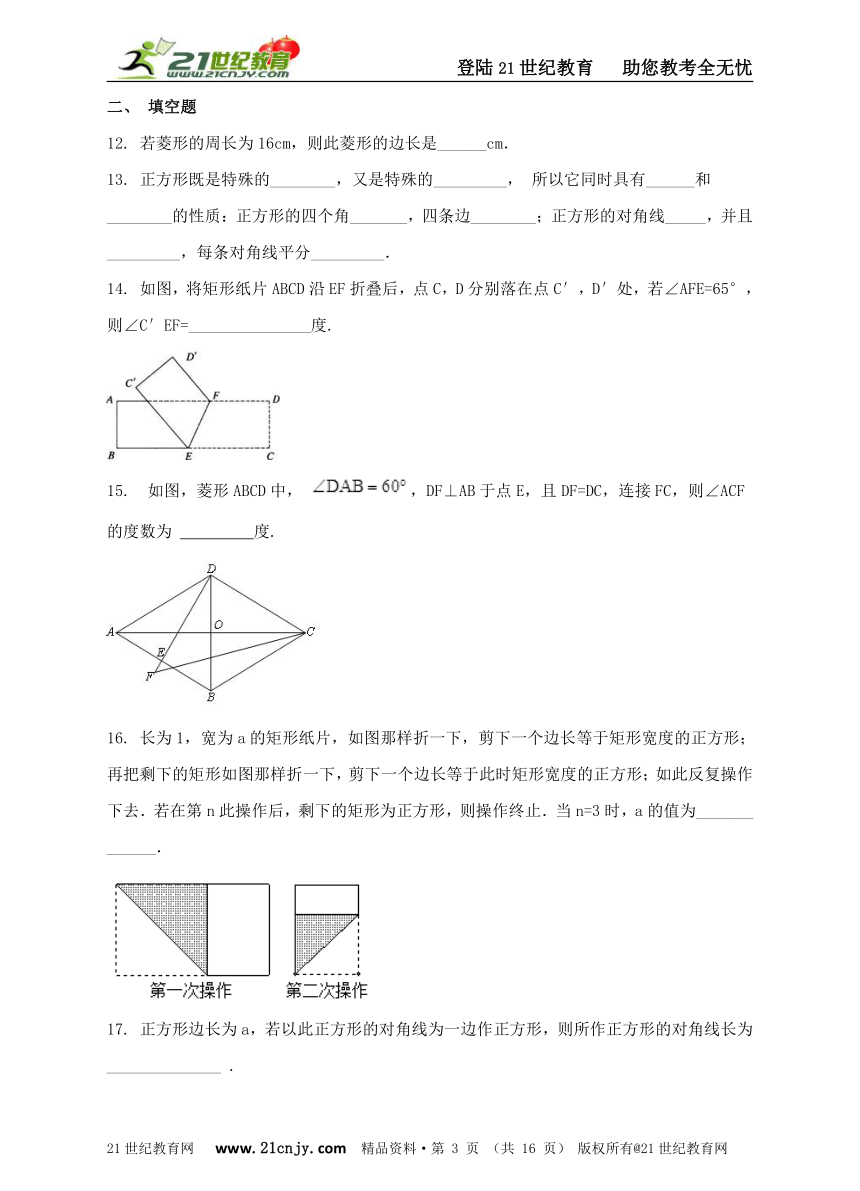
14. 如图，将矩形纸片ABCD沿EF折叠后，点C，D分别落在点C′，D′处，若∠AFE=65°，则∠C′EF=_______________度.
15. 如图，菱形ABCD中， ，DF⊥AB于点E，且DF=DC，连接FC，则∠ACF的度数为 ?? 度.
16. 长为1，宽为a的矩形纸片，如图那样折一下，剪下一个边长等于矩形宽度的正方形；再把剩下的矩形如图那样折一下，剪下一个边长等于此时矩形宽度的正方形；如此反复操作下去．若在第n此操作后，剩下的矩形为正方形，则操作终止．当n=3时，a的值为_______ ______．
17. 正方形边长为a，若以此正方形的对角线为一边作正方形，则所作正方形的对角线长为 ______________ .
18. 菱形两邻角的度数之比为12，较长对角线为20cm，则两对角线的交点到一边的距离为________________ cm.
19. 已知AD是△ABC的角平分线，E、F分别是边AB、AC的中点，连接DE、DF，在不再连接其他线段的前提下，要使四边形AEDF成为菱形，还需添加一个条件，这个条件可以是_________________ ；
三、 解答题
20. 如图所示，在菱形ABCD中，BE⊥AD，BF⊥CD，E，F为垂足，AE=ED，求∠EBF的度数．

21. 已知：如图，在□ABCD中，AC，BD交于点O，EF过点O，分别交CB，AD的延长线于点E，F，求证：AE=CF ． 21·世纪*教育网
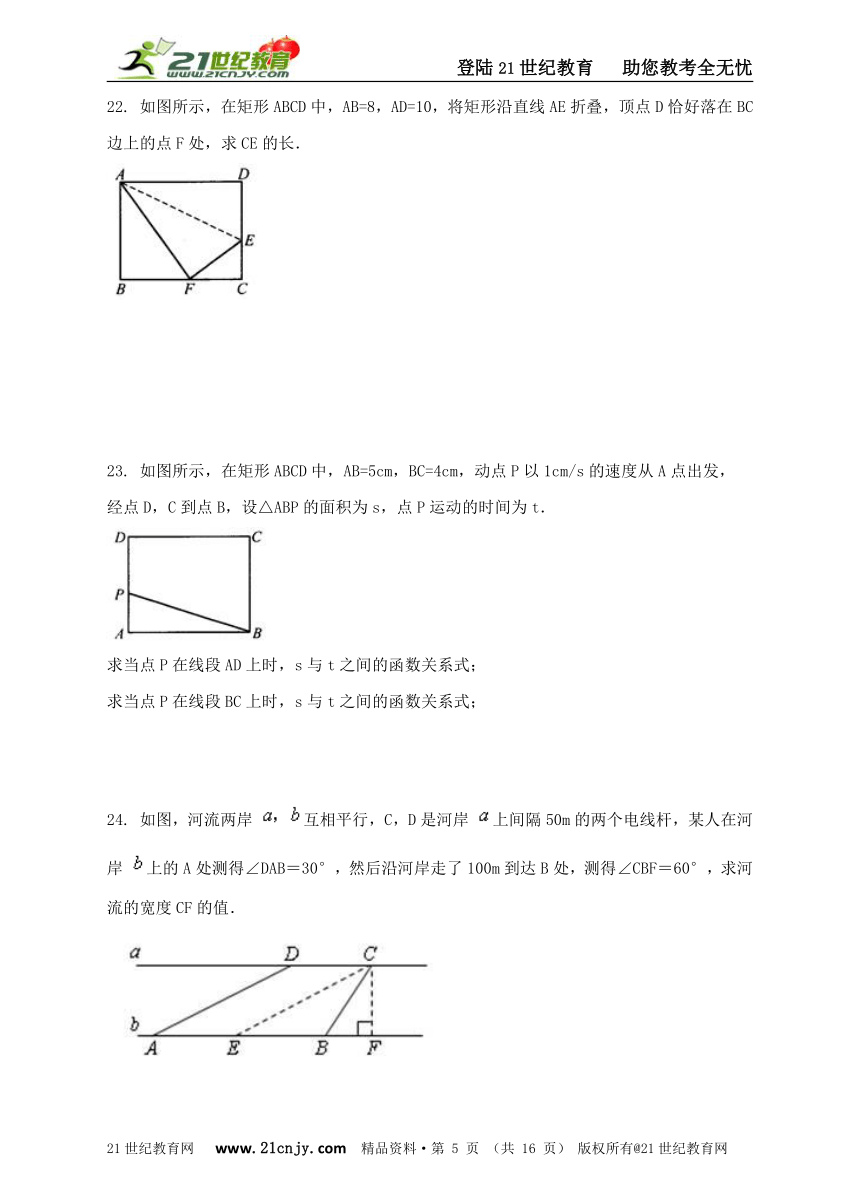
22. 如图所示，在矩形ABCD中，AB=8，AD=10，将矩形沿直线AE折叠，顶点D恰好落在BC边上的点F处，求CE的长． ? 21*cnjy*com
23. 如图所示，在矩形ABCD中，AB=5cm，BC=4cm，动点P以1cm/s的速度从A点出发，经点D，C到点B，设△ABP的面积为s，点P运动的时间为t． 求当点P在线段AD上时，s与t之间的函数关系式； 求当点P在线段BC上时，s与t之间的函数关系式； www-2-1-cnjy-com
24. 如图，河流两岸 互相平行，C，D是河岸 上间隔50m的两个电线杆，某人在河岸 上的A处测得∠DAB＝30°，然后沿河岸走了100m到达B处，测得∠CBF＝60°，求河流的宽度CF的值．21·cn·jy·com

25. 如图所示，在菱形ABCD中，已知E是BC上一点，且AE=AB，∠EAD=2∠BAE，  求证：BE=AF．
26. 已知：如图，在正方形ABCD中，G是CD上一点，延长BC到E，使CE＝CG，连接BG并延长交DE于F． 求证：△BCG≌△DCE； 将△DCE绕点D顺时针旋转90°得到△DAE′，判断四边形E′BGD是什么特殊四边形并说明理由？21教育网
答案解析
一、选择题
1、B 分析：先连接AC、BD，由于E、H是AB、AD中点，利用三角形中位线定理可知EH∥BD，同理易得FG∥BD，那么有EH∥FG，同理也有EF∥HG，易证四边形EFGH是平行四边形，而四边形ABCD是菱形，利用其性质有AC⊥BD，就有∠AOB=90°，再利用EF∥AC以及EH∥BD，两次利用平行线的性质可得∠HEF=∠BME=90°，即可证得结果． 解：如右图所示，四边形ABCD是菱形，顺次连接个边中点E、F、G、H，连接AC、BD， ∵E、H是AB、AD中点， ∴EH∥BD， 同理有FG∥BD， ∴EH∥FG， 同理EF∥HG， ∴四边形EFGH是平行四边形， ∵四边形ABCD是菱形， ∴AC⊥BD， ∴∠AOB=90°， 又∵EF∥AC， ∴∠BME=90， ∵EH∥BD， ∴∠HEF=∠BME=90°， ∴四边形EFGH是矩形， 故选B.21cnjy.com
2、B 分析：根据菱形的性质结合对角线AC=2，可得△ABC是等边三角形，即可得到结果. 解：∵菱形ABCD的周长为8， ∴AB=BC=2，， ∵AC=2， ∴△ABC是等边三角形， ∴∠ABC=60°， 故选B.【来源：21cnj*y.co*m】
3、 解析： 本题综合考查对角线在各种图形中的识别方法.
答案： B
4、B
解：在四边形ABCD中，AC⊥BD，连接各边的中点E，F，G，H， 则形成中位线EG∥AC，FH∥AC，EF∥BD，GH∥BD， 又因为对角线AC⊥BD， 所以GH⊥EG，EG⊥EF，EF⊥FH，FH⊥HG， 根据矩形的定义可以判定该四边形为矩形．故选B．www.21-cn-jy.com
5、C 分析：根据正方形的性质以及菱形的性质即可判断． 解：正方形和菱形都满足：四条边都相等，对角线平分一组对角，对角线垂直且互相平分； 菱形的对角线不一定相等，而正方形的对角线一定相等． 故选C．【版权所有：21教育】
6、C. 解：根据正方形、菱形、平行四边形的定义知A、B、D正确；C.如图所示直角梯形，使AB=AC，则满足是一组对边相等且有一个角是直角的四边形，但不是矩形.
7、B
解：在菱形ABCD中， ∵∠BAD=120°， ∴∠B=60°， ∴AB=AC=4， ∴菱形ABCD的周长=4AB=4×4=16． 故选B．
8、C
解：A.因为正方形图案的边长为7，同时还可用 来表示，故正确； ?? B.因为正方形图案面积从整体看是，从组合来看，可以是 ，还可以是 ，所以有 即 ， 所以 ，即；C. ，故?是错误的；D.由B可知．故选C．
9、C 分析：先根据菱形的性质求得∠BAD=60°，AO=3，即可得到△ABD为等边三角形，根据等边三角形可得AB的长，从而求得结果. 解：∵菱形ABCD，∠ADC=120°，AC=6， ∴AB=AD，∠BAD=60°，AO=3，∠AOB=90° ∴△ABD为等边三角形，∠BAO=30°， ∴AB=2BO， ∵ ，解得 ， ∴菱形的周长是 ， 故选C.
10、
解: 由题意知,BF=BE=DE,设AE=x,则BE=9-x,
在Rt△ABE中,有3 2 +x 2 =(9-x) 2 ,解得x=4,∴BF=BE=5.作EG⊥BF于G,则BG=AE=4,GF=BF-BG=1,
∴由勾股定理得,EF=
11、D
解： ∵铺成2×2的近似正方形，有完整菱形5个，5＝2 2 +1 2 ；
铺成3×3的近似正方形，有完整菱形13个，13＝3 2 +2 2 ；
铺成4×4的近似正方形，有完整菱形25个，25＝4 2 +3 2 ；
∴铺成 n × n 的近似正方形，有完整菱形个数为 n 2 +( n －1) 2 ，当有完整菱形181个时，经试数知 n ＝10．2-1-c-n-j-y
二、填空题
12、4 分析：根据菱形的性质即可得到结果. 解：由题意得此菱形的边长是16÷4=4cm．
13、解：矩形，菱形，矩形，菱形，（1）都是直角，相等；（2）相等，互相垂直平分，一组对角
14、解：因为在矩形ABCD中，所以AD∥BC，所以∠CEF=∠AFE=65°.又因为将矩形纸片ABCD沿EF折叠后，点C，D分别落在点C′，D′处，所以∠C′EF=∠CEF=65°.
15、分析：利用菱形的性质得出∠DCB的度数，再利用等腰三角形的性质得出∠DCF的度数，进而得出答案： 解：∵菱形ABCD中，∠DAB=60°，DF=DC，∴∠BCD=60°，AB∥CD，∠DFC=∠DCF. ∵DF⊥AB于点E，∴∠FDC=90°.∴∠FDC=∠DCF=45°. ∵菱形ABCD中，∠DCA=∠ACB，∴∠DCA=∠ACB=30°. ∴∠ACF的度数为：45°-30°=15°． 21世纪教育网版权所有
16、分析：根据操作步骤，可知每一次操作时所得正方形的边长都等于原矩形的宽．所以首先需要判断矩形相邻的两边中，哪一条边是矩形的宽．当 时，矩形的长为1，宽为a，所以第一次操作时所得正方形的边长为a，剩下的矩形相邻的两边分别为1-a，a．由1-a＜a可知，第二次操作时所得正方形的边长为1-a，剩下的矩形相邻的两边分别为1-a，a-（1-a）=2a-1．由于（1-a）-（2a-1）=2-3a，所以（1-a）与（2a-1）的大小关系不能确定，需要分情况进行讨论．又因为可以进行三次操作，故分两种情况：①1-a＞2a-1；②1-a＜2a-1．对于每一种情况，分别求出操作后剩下的矩形的两边，根据剩下的矩形为正方形，列出方程，求出a的值． 解：由题意，可知当时，第一次操作后剩下的矩形的长为a，宽为1-a，所以第二次操作时正方形的边长为1-a，第二次操作以后剩下的矩形的两边分别为1-a，2a-1．此时，分两种情况： ①如果1-a＞2a-1，即a＜，那么第三次操作时正方形的边长为2a-1． ∵经过第三次操作后所得的矩形是正方形， ∴矩形的宽等于1-a， 即2a-1=（1-a）-（2a-1），解得a=； ②如果1-a＜2a-1，即a＞，那么第三次操作时正方形的边长为1-a． 则1-a=（2a-1）-（1-a），解得a=． 17、2a 分析：根据正方形的性质、勾股定理结合正方形的面积公式即可求得结果. 解：由题意得此正方形的对角线长 则所作正方形的对角线长
18、5 分析：先根据菱形的性质求得邻角的度数，再根据菱形的对角线平分对角结合对角线互相平分即可求得结果. 解：∵菱形两邻角的度数之比为12， ∴邻角的度数分别为60°、120° ∴较长对角线分60°所成的两个小角均为30° ∵较长对角线为20cm ∴对角线的一半为10cm ∴两对角线的交点到一边的距离为5cm.
19、答案不唯一，如AB=AC 分析：菱形的判定方法有三种：①定义：一组邻边相等的平行四边形是菱形；②四边相等的四边形是菱形；③对角线互相垂直平分的四边形是菱形． 解：由题意知，可添加：AB=AC． 则三角形是等腰三角形， 由等腰三角形的性质知，顶角的平分线与底边上的中线重合， 即点D是BC的中点， ∴DE，EF是三角形的中位线， ∴DE∥AB，DF∥AC， ∴四边形ADEF是平行四边形， ∵AB=AC， 点E，F分别是AB，AC的中点， ∴AE=AF， ∴平行四边形ADEF为菱形．
三、解答题
20、分析：依题意，首先推出△ABD是等边三角形，然后可知∠A=60°，∠EBF+∠D=180°，∠D+∠A=180°，故可得∠EBF=∠A=60°． 解：如图，连接BD． ∵BE⊥AD，AE=ED， ∴BD=AB=AD， ∴△ABD是等边三角形， ∴∠A=60°， 又∵BE⊥AD，BF⊥CD， ∴∠BED+∠BFD=180°， ∴∠D+∠EBF=180°， 又∵∠D+∠A=180°， ∴∠EBF=∠A=60°．
21、分析：可先根据平行四边形的性质证得△BOE≌△DOF，得出BE=DF，进而可得△ABE≌△CDF，从而得到结果． 解：在平行四边形ABCD中，OB=OD，∠DFO=∠BEO，∠BOE=∠DOF， ∴△BOE≌△DOF，（AAS） ∴BE=DF， 又AB=CD，∠ABE=∠CDF， ∴△ABE≌△CDF（SAS）， ∴AE=CF．
22、分析：在△ABF中，利用勾股定理可求得BF的长，进而可求得CF长；同理在△CEF中，利用勾股定理可求得CE长． 解：∵四边形ABCD是矩形， ∴∠B=∠C=90°，AD=BC=10，CD=AB=8． ∵△AEF是△ADE翻折得到的， ∴AF=AD=10，EF=DE， ∴BF=6， ∴FC=4， ∵FC2+CE2=EF2， ∴42+CE2=（8-CE）2， 解得CE=3．
23、分析：根据直角三角形的面积公式即可得到结果. 解：（1）∵四边形ABCD是矩形， ∴∠A=90°，BC=4cm， ∴ ； （2）∵四边形ABCD是矩形， ∴∠ABC=90°，AD= ∴
24、解：过点C作CE ?AD，交AB于E ?CD??AE,CE??AD 四边形AECD是平行四边形。 AE="CD=50m,EB=AB-AE=50m," CEB=DAB= 又CBF= ?,故ECB=,CB=EB=50m 在直角三角形CFB中，CF=CB sinCBF=50sin 43m，
25、分析：根据菱形的性质可得AD∥BC，即得∠EAD=∠BEA，再结合AE=AB，∠EAD=2∠BAE，根据三角形的内角和为180°即可证得结果. 解：∵菱形ABCD， ∴AD∥BC， ∴∠EAD=∠BEA， ∵∠EAD=2∠BAE， ∴∠BEA=2∠BAE， ∵AE=AB， ∴∠ABE=∠BEA， 设∠BAE=x，则∠ABE=∠BEA=2x， 则5x=180°，解得x=36°， ∴∠BAE=36°，∠ABE=∠BEA=72°， ∵菱形ABCD， ∴AD=AB， ∴∠ABD=∠ADB， ∵AD∥BC， ∴∠ADB=∠FBE， ∴∠ABD=∠FBE=36°， ∴∠BFE=72°， ∵∠BFE=∠BEA=72°， ∴BE=AF．
26、（1）证明：∵四边形为正方形， ∴BC＝CD，∠BCG＝∠DCE＝90° ， ∵CG＝CE， ∴△BCG≌△DCE． （2）四边形E′BGD是平行四边形 ． 理由： ∵△DCE绕点D顺时针旋转90°得到△DAE′， ∴CE＝AE′， ∵CG＝CE， ∴CG＝AE′， ∵AB＝CD，AB∥CD， ∴BE′＝DG，BE′∥DG， ∴四边形E′BGD是平行四边形 ． （1）由正方形ABCD，得BC=CD，∠BCD=∠DCE=90°，又CG=CE，所以△BCG≌△DCE（SAS）． （2）由（1）得BG=DE，又由旋转的性质知AE′=CE=CG，所以BE′=DG，从而证得四边形E′BGD为平行四边形