1.1 二次根式 课件

课件31张PPT。第1章 二次根式1.1 二次根式1课堂讲解二次根式的定义
二次根式有意义的条件
二次根式的“双重”非负性( ≥0，a≥0)2课时流程逐点
导讲练课堂小结作业提升学习目标新课导入 球网的高AD为2.43米，AC=AB，CB为a米。你能用代数式表示AC的长吗？复习旧知2、0的平方根是什么？算术平方根是什么？1、3的平方根是什么？算术平方根是什么？4、一个非负数a的算术平方根应如何表示？1知识点二次根式的定义 我们知道，正数的正平方根和零的平方根统称算术
平方根，用 (a≥0)表示.
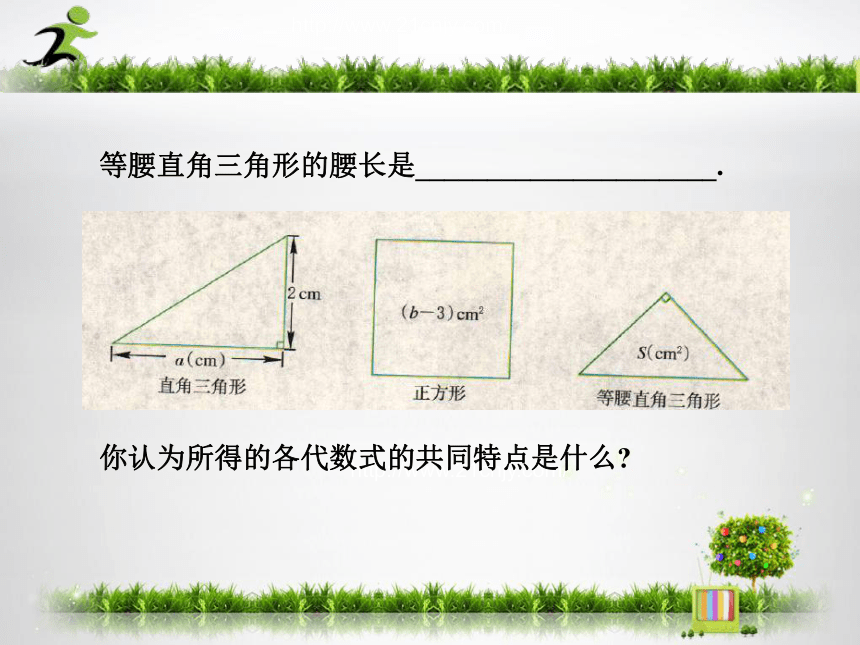
根据下图所示的直角三角形、正方形和等腰直角三
角形的条件，完 成以下填空：
直角三角形的斜边长是_____________________；
正方形的边长是_____________________；
感悟新知等腰直角三角形的腰长是_____________________.
你认为所得的各代数式的共同特点是什么? 像 这样表示算术平方根的
代数式叫做二次根式.定义：像 这样表示算术平方根的代
数式叫做二次根式，其中二次根式 中的“ ”称为二
次根号，a称为被开方数(式)．
要点精析：
(1)二次根式的定义是从式子的结构形式上界定的，必须含
有二次根号“ ”；“ ”的根指数为2，即 ，“2”
一般省略不写．
(2)被开方数a可以是一个数，也可以是一个含有字母的式
子，但前提是a必须大于或等于0. 判断下列各式是否为二次根式，并说明理由．例1判断一个式子是不是二次根式，实质是看它是否具备
二次 根式定义的条件，紧扣定义进行识别．一看根指数
是否为2，二看被开方数(式)是否为非负数．导引：(1)∵无论x为何值，都有x2＋1＞0，
∴ 是二次根式．
(2)当0≤0时，－5a≥0，∴ 是二次根式；
当a＞0时，－5a＜0，∴ 不是二次根式．
∴ 不一定是二次根式．
(3)当x＝－3时， 无意义，
∴ 也无意义；
当x≠－3时， ＞0，解： ∴ 是二次根式．
∴ 不一定是二次根式．
(4)当a＝4时，－(a－4)2＝0，
∴ 是二次根式；
当a≠4时，－(a－4)2＜0，∴ 不是二次根式．
∴ 不一定是二次根式．
(5)∵x2＋2x＋2＝x2＋2x＋1＋1＝(x＋1)2＋1＞0，
∴ 是二次根式． 二次根式的识别方法：判断一个式子是否为二次根
式，一定要紧扣二次根式的定义，看所给的式子是否同
时具备二次根式的两个特征：(1)含根号且根指数为2(通
常省略不写)；(2)被开方数(式)为非负数．下列各式中，一定是二次根式的是（ ）练习1下列式子不一定是二次根式的是(　　)下列式子：
中，是二次根式的有(　　)
A．2个 B．3个
C．4个 D．5个2知识点二次根式有意义的条件(1)式子 只有在条件a≥0时才叫二次根式．即a≥0是
为二次根式的前提条件.式子 就不是二次根式，
但式子 却又是二次根式．
（a≥0）实际上就是非负数a的算术平方根，既可
表示开方运算,也可表示运算的结果.同时 （a≥0）
也是一个非负数，我们把这个性质叫做二次根式的
双重非负性.1.二次根式有意义的条件是被开方数(式)为非负数，反
之也成立，即 有意义? a≥0.
2.二次根式无意义的条件是被开方数(式)为负数，反之
也成立，即 无意义? a＜0.要点精析：
(1)如果一个式子含有多个二次根式，那么它有意义的条件
是：各个二次根式中的被开方数(式)都必须是非负数．
(2)如果一个式子既含有二次根式又含有分式，那么它有意
义的条件是：二次根式中的被开方数(式)是非负数，分
式的分母不等于0．
(3)如果一个式子含有零指数幂或负整数指数幂，那么它有
意义的条件是：底数不为0．求下列二次根式中字母a的取值范围.例2解：(1)由 a+1≥0，得 a≥ -1，所以字母a的取值范围是大
于或等于- 1的实数.
(2)由 > 0，得 1 - 2a > 0，即 a< .
所以字母a的取值范围是小于 的实数.
(3)因为无论a取何值，都有(a-3) 2 ≥ 0,所以a的取值范
围是全体实数. 求式子有意义时字母的取值范围的方法：第一步，明确
式子有意义的条件，对于单个的二次根式，则必须满足被开
方数为非负数；对于含有多个二次根式的，则必须满足多个
被开方数同时为非负数；对于零指数幂或负整数指数幂，则
必须满足底数不能为零；对于含有分式的，则必须满足分母
不能为零．第二步，利用式子中所有有意义的条件，建立不
等式或不等式组．第三步，求出不等式或不等式组的解集，
即为字母的取值范围．求下列二次根式中字母x的取值范围.练习2要使二次根式 有意义，x必须满足(　　)
A．x≤2 B．x≥2
C．x＜2 D．x＞2要使式子 有意义，则m的取值范围是(　　)
A．m>－1
B．m≥－1
C．m>－1且m≠1
D．m≥－1且m≠1当x= -4时，求二次根式 的值.例3解：将x= - 4代入二次根式，得本题运用类比思想．求二次根式的值与求有理式的值的
方法一样，代入数值计算即可．但要注意被开方数必须
是非负数．当x分别取下列值时，求 的值．
(1)x＝ ；　(2)x＝－1；　(3)x＝1.练习3如果式子 有意义，那么x的取值范围在数轴上表示出来，正确的是(　　)3知识点二次根式的“双重”非负性( ≥0，a≥0) （a≥0） 是一个非负数.
1.理解二次根式的非负性应从算术平方根入手，当a≥0时，
表示a的算术平方根，因此 ≥0 .所以“二次根式”
包含有两个“非负”即：①被开方数非负：a≥0；②二
次根式的值非负： ≥0.
2.若 =0,则 a=0,b=0.由于二次根式 和 都是
非负数，所以它们的值都为0.若 ，则 x-y 的值为 （ ）
A．1 B．－1 C．7 D．－7例4根据非负数的性质列式求出x、y的值，然后代入代数
式进行计算即可得解．因为 都
是非负数，它们的和为0，所以（y+3)2=0，
，所以y+3=0，x+y-1=0，解得y=-3，x=4，
所以x-y=7，故选C．导引：C两个非负数的和为0时，这两个非负数都为0．若 ，求a2012+b2012的值．练习4若 ＋(y＋2)2＝0，则(x＋y)2 016等于(　　)
A．－1 B．1
C．32 016 D．－32 0161.二次根式的条件：
(1)带二次根号“ ”；
(2)被开方数是非负数．
2.常见具有“非负性”的三类数： ，|a|，a2n(n为正
整数)；二次根式的双重非负性为：
(1) ≥0；(2)a≥0.)课堂小结 3. 转化思想一个概念：二次根式
两类题型：
1. 求代数式所含字母的取值范围
2. 求二次根式的值
三点注意：
1. 二次根式的双重非负性
2. 分母不能为0 列不等式（组）1.完成教材P5课内练习T2，
教材P5-P6作业题T1-T6
2.请完成练习册对应习题课后作业