第二章一元二次方程单元测试题

浙教版八年级下数学第二章一元二次方程
一．选择题（共10小题）
1．下列方程中，关于x的一元二次方程是（　　）
A．（x+1）2=2（x+1） B． C．ax2+bx+c=0 D．x2+2x=x2﹣1
2．已知x=1是关于x的一元二次方程2x2﹣x+a=0的一个根，则a的值是（　　）
A．2 B．﹣2 C．1 D．﹣1
3．一元二次方程x2﹣6x﹣5=0配方可变形为（　　）
A．（x﹣3）2=14 B．（x﹣3）2=4 C．（x+3）2=14 D．（x+3）2=4
4．关于x的一元二次方程（m﹣1）x2+5x+m2﹣3m+2=0，常数项为0，则m值等于（　　）
A．1 B．2 C．1或2 D．0
5．关于x的方程ax2+bx+c=3的解与（x﹣1）（x﹣4）=0的解相同，则a+b+c的值为（　　）
A．2 B．3 C．1 D．4
6．若a，b是方程x2+2x﹣2016=0的两根，则a2+3a+b=（　　）
A．2016 B．2015 C．2014 D．2012
7．已知一元二次方程x2﹣3x﹣3=0的两根为α与β，则的值为（　　）
A．﹣1 B．1 C．﹣2 D．2
8．公园有一块正方形的空地，后来从这块空地上划出部分区域栽种鲜花（如图），原空地一边减少了1m，另一边减少了2m，剩余空地的面积为18m2，求原正方形空地的边长．设原正方形的空地的边长为xm，则可列方程为（　　）21世纪教育网版权所有
A．（x+1）（x+2）=18 B．x2﹣3x+16=0
C．（x﹣1）（x﹣2）=18 D．x2+3x+16=0
9．若关于x的一元二次方程x2﹣2x+kb+1=0有两个不相等的实数根，则一次函数y=kx+b的大致图象可能是（　　）21·cn·jy·com
A． B． C． D．
10．如图的六边形是由甲、乙两个长方形和丙、丁两个等腰直角三角形所组成，其中甲、乙的面积和等于丙、丁的面积和．若丙的一股长为2，且丁的面积比丙的面积小，则丁的一股长为何？（　　）www.21-cn-jy.com
A． B． C．2﹣ D．4﹣2
　
二．填空题（共6小题）
11．若关于x的方程（a﹣1）=1是一元二次方程，则a的值是　 　．
12．关于x的一元二次方程（k﹣1）x2﹣2x+1=0有两个不相等的实数根，
则实数k的取值范围是　 　．
13．若一元二次方程ax2﹣bx﹣2015=0有一根为x=﹣1，则a+b=　 　．
14．三角形的两边长分别是3和4，第三边长是方程x2﹣13x+40=0的根，
则该三角形的周长为　 　．
15．某楼盘2013年房价为每平方米8100元，经过两年连续降价后，2015年房价为7600元．设该楼盘这两年房价平均降低率为x，根据题意可列方程为　 　．
16．对于实数a，b，定义运算“﹡”：a﹡b=．例如4﹡2，因为4＞2，
所以4﹡2=42﹣4×2=8．若x1，x2是一元二次方程x2﹣5x+6=0的两个根，则x1﹡x2= 　．
　
三．解答题（共7小题）
17．解方程：
（1）x2﹣3x﹣1=0． （2）x2+4x﹣2=0．
18．已知关于x的方程（x﹣3）（x﹣2）﹣p2=0．
（1）求证：无论p取何值时，方程总有两个不相等的实数根；
（2）设方程两实数根分别为x1，x2，且满足x12+x22=3x1x2，求实数p的值．
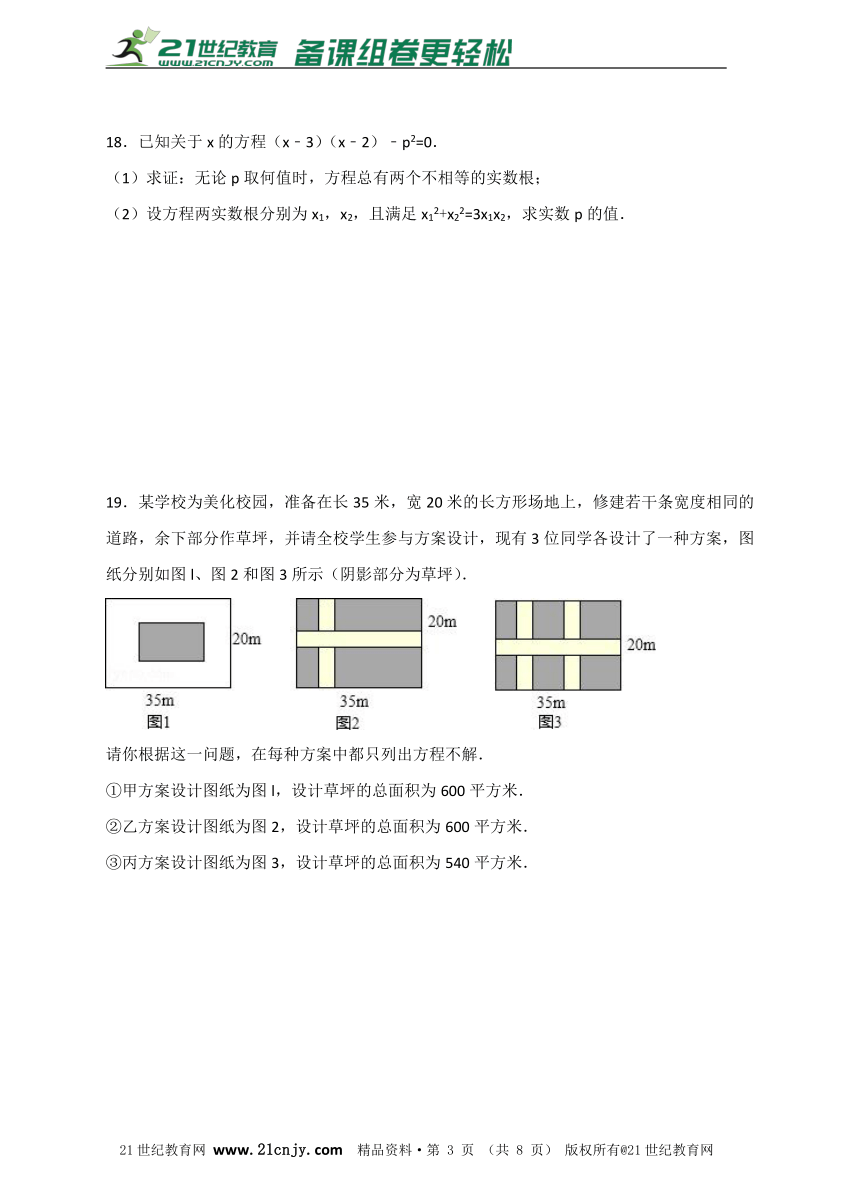
19．某学校为美化校园，准备在长35米，宽20米的长方形场地上，修建若干条宽度相同的道路，余下部分作草坪，并请全校学生参与方案设计，现有3位同学各设计了一种方案，图纸分别如图l、图2和图3所示（阴影部分为草坪）．2·1·c·n·j·y
请你根据这一问题，在每种方案中都只列出方程不解．
①甲方案设计图纸为图l，设计草坪的总面积为600平方米．
②乙方案设计图纸为图2，设计草坪的总面积为600平方米．
③丙方案设计图纸为图3，设计草坪的总面积为540平方米．
20．某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利45元，为了扩大销售、增加盈利尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出4件，若商场平均每天盈利2100元，每件衬衫应降价多少元？请完成下列问题：【来源：21·世纪·教育·网】
（1）未降价之前，某商场衬衫的总盈利为　　 元．
（2）降价后，设某商场每件衬衫应降价x元，则每件衬衫盈利　　元，平均每天可售出　　件（用含x的代数式进行表示）21·世纪*教育网
（3）请列出方程，求出x的值．
21．如图，等腰直角三角形ABC中，∠B=90°，AB=BC=8cm，动点P从A出发沿AB向B移动，通过点P引PQ∥AC，PR∥BC，问当AP等于多少时，平行四边形PQCR的面积等于16cm2？设AP的长为xcm，列出关于x的方程．21cnjy.com
22．阅读下列材料：
（1）关于x的方程x2﹣3x+1=0（x≠0）方程两边同时乘以得：即，
（2）a3+b3=（a+b）（a2﹣ab+b2）；a3﹣b3=（a﹣b）（a2+ab+b2）．
根据以上材料，解答下列问题：
（1）x2﹣4x+1=0（x≠0），则=　　，=　　，=　　；
（2）2x2﹣7x+2=0（x≠0），求的值．
23．某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元，为扩大销售增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价一元，市场每天可多售2件，问他降价多少元时，才能使每天所赚的利润最大？并求出最大利润．21教育网
　

浙教版八年级下数学第二章一元二次方程
参考答案与试题解析
　
一．选择题（共10小题）
1．解：下列方程中，关于x的一元二次方程是（x+1）2=2（x+1），故选A．
2．解：∵x=1是关于x的一元二次方程2x2﹣x+a=0的一个根，
∴x=1满足关于x的一元二次方程2x2﹣x+a=0，
∴2×12﹣1+a=0，即1+a=0，解得，a=﹣1；故选D．
3．解：x2﹣6x﹣5=0，x2﹣6x=5，x2﹣6x+9=5+9，（x﹣3）2=14，故选：A．
5．解：∵方程（x﹣1）（x﹣4）=0，∴此方程的解为x1=1，x2=4，
∵关于x的方程ax2+bx+c=3与方程（x﹣1）（x﹣4）=0的解相同，
∴把x1=1代入方程得：a+b+c=3，故选B．
6．解：∵a是方程x2+2x﹣2016=0的实数根，
∴a2+2a﹣2016=0，∴a2=﹣2a+2016，∴a2+3a+b=﹣2a+2016+3a+b=a+b+2016，
∵a、b是方程x2+2x﹣2016=0的两个实数根，
∴a+b=﹣2，∴a2+3a+b=﹣2+2016=2014．故选：C．
7．解：根据题意得α+β=3，αβ=﹣3，所以===﹣1．故选A．
8．解：设原正方形的边长为xm，依题意有（x﹣1）（x﹣2）=18，故选C．
9．解：∵x2﹣2x+kb+1=0有两个不相等的实数根，
∴△=4﹣4（kb+1）＞0，解得kb＜0，
A．k＞0，b＞0，即kb＞0，故A不正确；
B．k＞0，b＜0，即kb＜0，故B正确；
C．k＜0，b＜0，即kb＞0，故C不正确；
D．k＜0，b=0，即kb=0，故D不正确；故选：B．
10．解：设丁的一股长为a，且a＜2，
∵甲面积+乙面积=丙面积+丁面积，
∴2a+2a=×22+×a2，∴4a=2+a2，∴a2﹣8a+4=0，
∴a===4±2，
∵4+2＞2，不合题意舍，4﹣2＜2，合题意，∴a=4﹣2．故选D．
二．填空题（共6小题）
12．解：∵关于x的一元二次方程（k﹣1）x2﹣2x+1=0有两个不相等的实数根，
∴k﹣1≠0且△=（﹣2）2﹣4（k﹣1）＞0，解得：k＜2且k≠1．故答案为：k＜2且k≠1．
13．解：把x=﹣1代入一元二次方程ax2﹣bx﹣2015=0得：a+b﹣2015=0，
即a+b=2015．故答案是：2015．
14．解：x2﹣13x+40=0，（x﹣5）（x﹣8）=0，所以x1=5，x2=8，
而三角形的两边长分别是3和4，所以三角形第三边的长为5，
所以三角形的周长为3+4+5=12．故答案为12．
15．解：设该楼盘这两年房价平均降低率为x，根据题意列方程得：
8100×（1﹣x）2=7600，故答案为：8100×（1﹣x）2=7600．
16．解：∵x1，x2是一元二次方程x2﹣5x+6=0的两个根，
∴（x﹣3）（x﹣2）=0，解得：x=3或2，
①当x1=3，x2=2时，x1﹡x2=32﹣3×2=3；
②当x1=2，x2=3时，x1﹡x2=3×2﹣32=﹣3．故答案为：3或﹣3．
三．解答题（共7小题）
17．解：（1）∵a=1，b=﹣3，c=﹣1，∴b2﹣4ac=9+4=13，
∴x=，∴方程的解为：x1=，x2=；
（2）移项得：x2+4x=2，配方得：x2+4x+4=2+4，即（x+2）2=6，
∴x+2=±，∴x1=﹣2+，x2=﹣2﹣．
18．证明：（1）（x﹣3）（x﹣2）﹣p2=0，x2﹣5x+6﹣p2=0，
△=（﹣5）2﹣4×1×（6﹣p2）=25﹣24+4p2=1+4p2，
∵无论p取何值时，总有4p2≥0，
∴1+4p2＞0，∴无论p取何值时，方程总有两个不相等的实数根；
（2）x1+x2=5，x1x2=6﹣p2，∵x12+x22=3x1x2，
∴（x1+x2）2﹣2x1x2=3x1x2，∴52=5（6﹣p2），∴p=±1．
19．解：①设道路的宽为x米．依题意得：（35﹣2x）（20﹣2x）=600；
②设道路的宽为x米．依题意得：（35﹣x）（20﹣x）=600；
③设道路的宽为x米．依题意得：（35﹣2x）（20﹣x）=540．
20．解：（1）20×45=900，故答案为：900；
（2）降价后，设某商场每件衬衫应降价x元，则每件衬衫盈利（45﹣x）元，
平均每天可售出（20+4x）件，故答案为：（45﹣x）；（20+4x）；
（3）由题意得：（45﹣x）（20+4x）=2100，解得：x1=10，x2=30．
因尽快减少库存，故x=30．答：每件衬衫应降价30元．
21．解：设AP的长为xcm时，?PQCR的面积等于16cm2，依题意有x（8﹣x）=16．
22．解；（1）∵x2﹣4x+1=0，
∴x+=4，∴（x+）2=16，∴x2+2+=16，∴x2+=14，
∴（x2+）2=196，∴x4++2=196，∴x4+=194．
故答案为4，14，194．
（2）∵2x2﹣7x+2=0，∴x+=，x2+=，
∴=（x+）（x2﹣1+）=×（﹣1）=．