第五章特殊平行四边形单元测试题

浙教版八年级下数学第五章特殊平行四边形
　
一．选择题（共10小题）
1．如图，矩形ABCD的对角线交于点O，若∠ACB=30°，AB=2，则OC的长为（　　）
A．2 B．3 C．2 D．4
2．下列性质中，菱形具有而矩形不一定具有的是（　　）
A．对角线相等 B．对角线互相平分
C．对角线互相垂直 D．邻边互相垂直
3．如图，四边形ABCD是正方形，延长AB到点E，使AE=AC，则∠BCE的度数是（　　）
A．22.5° B．25°
C．23° D．20°
4．如图，在菱形ABCD中，对角线AC与BD相交于点O，若AB=2，∠ABC=60°，
则BD的长为（　　）
A．2 B．3
C． D．2
5．如图，四边形ABCD是菱形，AC=8，DB=6，DH⊥AB于H，则DH等于（　　）
A． B．
C．5 D．4
6．菱形ABCD的对角线AC，BD相交于点O，E，F分别是AD，CD边上的中点，连接EF．若EF=，BD=2，则菱形ABCD的面积为（　　）21世纪教育网版权所有
A．2 B．
C．6 D．8
7．如图，在矩形ABCD中，AB=4，BC=6，点E为BC的中点，将△ABE沿AE折叠，使点B落在矩形内点F处，连接CF，则CF的长为（　　）21教育网
A． B．
C． D．
8．已知菱形OABC在平面直角坐标系的位置如图所示，顶点A（5，0），OB=4，点P是对角线OB上的一个动点，D（0，1），当CP+DP最短时，点P的坐标为（　　）
A．（0，0） B．（1，）
C．（，） D．（，）
9．如图，在正方形ABCD中，△ABE和△CDF为直角三角形，∠AEB=∠CFD=90°，AE=CF=5，BE=DF=12，则EF的长是（　　）21cnjy.com
A．7
B．8
C．7
D．7
10．如图所示，矩形ABCD中，AE平分∠BAD交BC于E，∠CAE=15°，则下面的结论：
①△ODC是等边三角形；②BC=2AB；③∠AOE=135°；④S△AOE=S△COE，
其中正确结论有（　　）
A．1个 B．2个 C．3个 D．4个
　
二．填空题（共6小题）
11．已知正方形的边长为1cm，则其对角线长是　 　．
12．如图，菱形ABCD的对角线AC、BD相交于点O，E为AD的中点，若OE=3，则菱形ABCD的周长为　 　．【来源：21·世纪·教育·网】
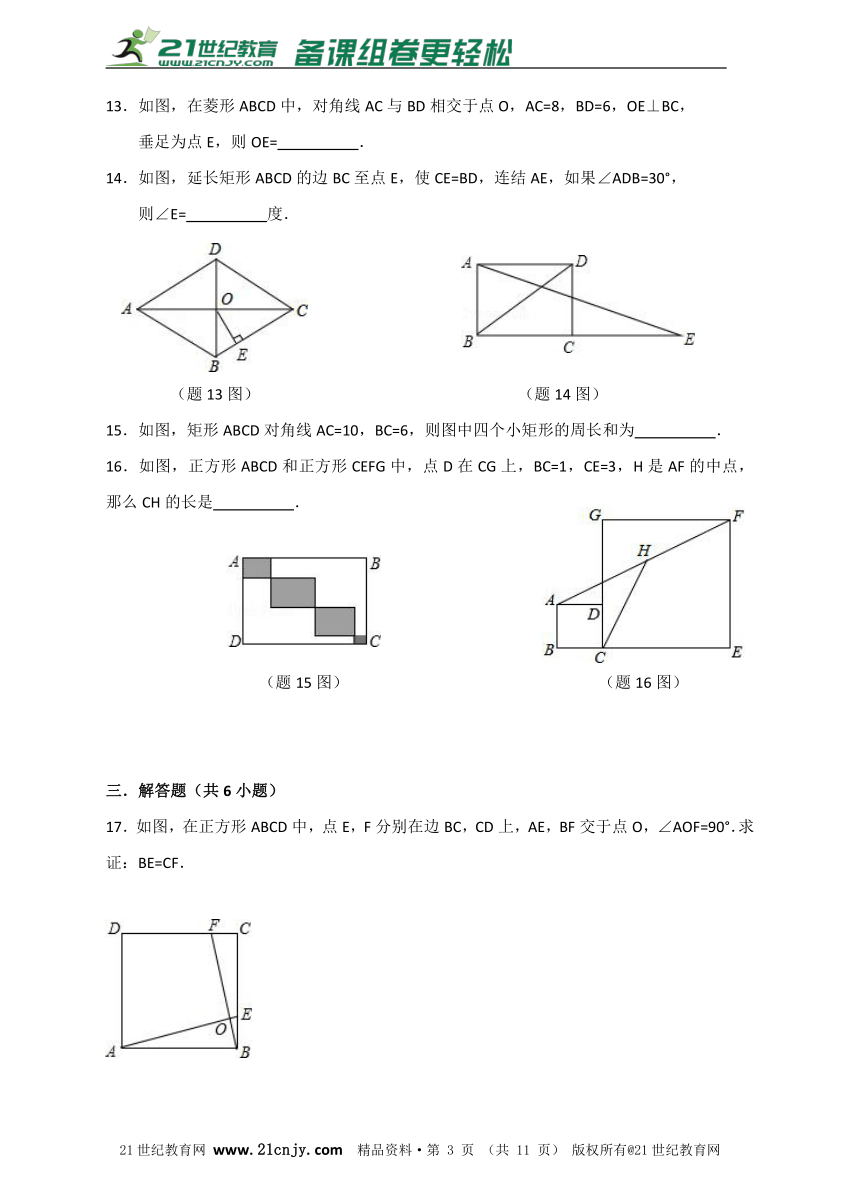
13．如图，在菱形ABCD中，对角线AC与BD相交于点O，AC=8，BD=6，OE⊥BC，
垂足为点E，则OE=　 　．
14．如图，延长矩形ABCD的边BC至点E，使CE=BD，连结AE，如果∠ADB=30°，
则∠E=　 　度．
（题13图） （题14图）
15．如图，矩形ABCD对角线AC=10，BC=6，则图中四个小矩形的周长和为　 　．
16．如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，H是AF的中点，那么CH的长是　 　．www.21-cn-jy.com
　
（题15图） （题16图）
三．解答题（共6小题）
17．如图，在正方形ABCD中，点E，F分别在边BC，CD上，AE，BF交于点O，∠AOF=90°．求证：BE=CF．21·cn·jy·com
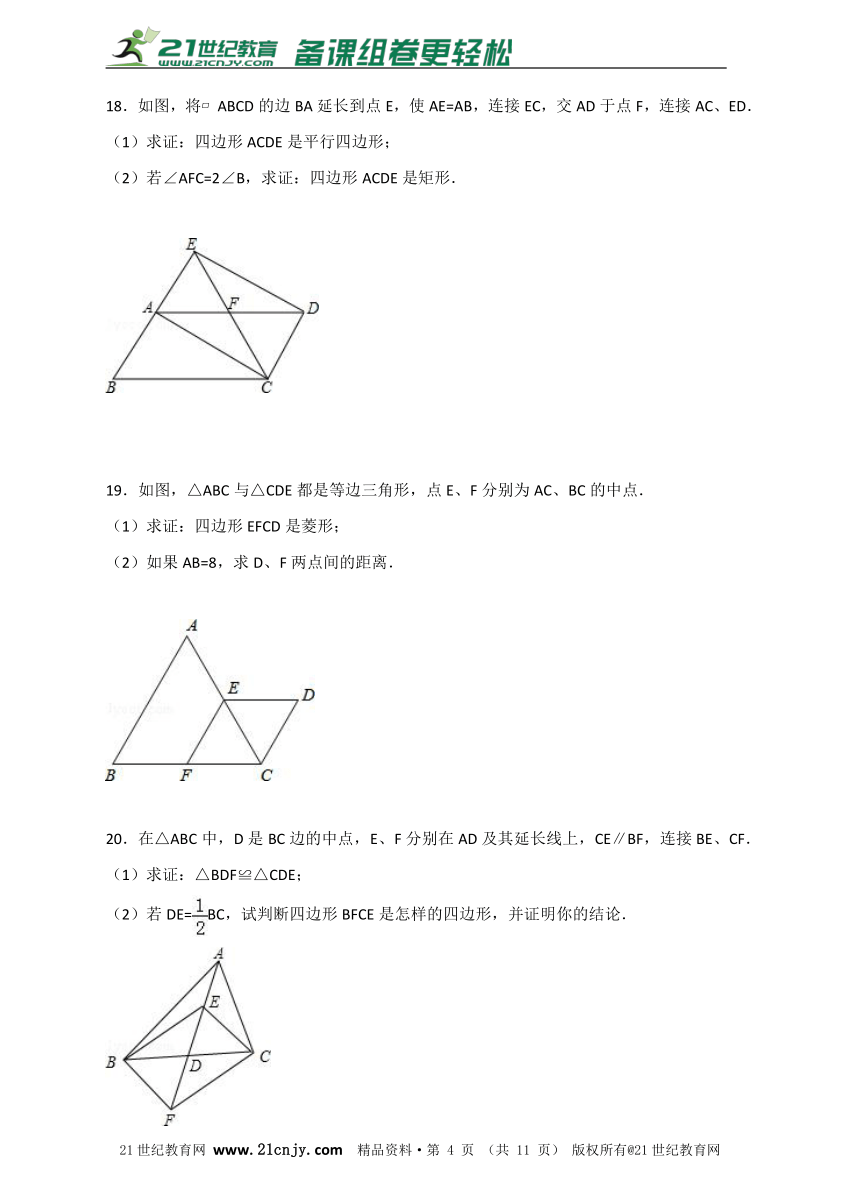
18．如图，将?ABCD的边BA延长到点E，使AE=AB，连接EC，交AD于点F，连接AC、ED．
（1）求证：四边形ACDE是平行四边形；
（2）若∠AFC=2∠B，求证：四边形ACDE是矩形．
19．如图，△ABC与△CDE都是等边三角形，点E、F分别为AC、BC的中点．
（1）求证：四边形EFCD是菱形；
（2）如果AB=8，求D、F两点间的距离．
20．在△ABC中，D是BC边的中点，E、F分别在AD及其延长线上，CE∥BF，连接BE、CF．
（1）求证：△BDF≌△CDE；
（2）若DE=BC，试判断四边形BFCE是怎样的四边形，并证明你的结论．
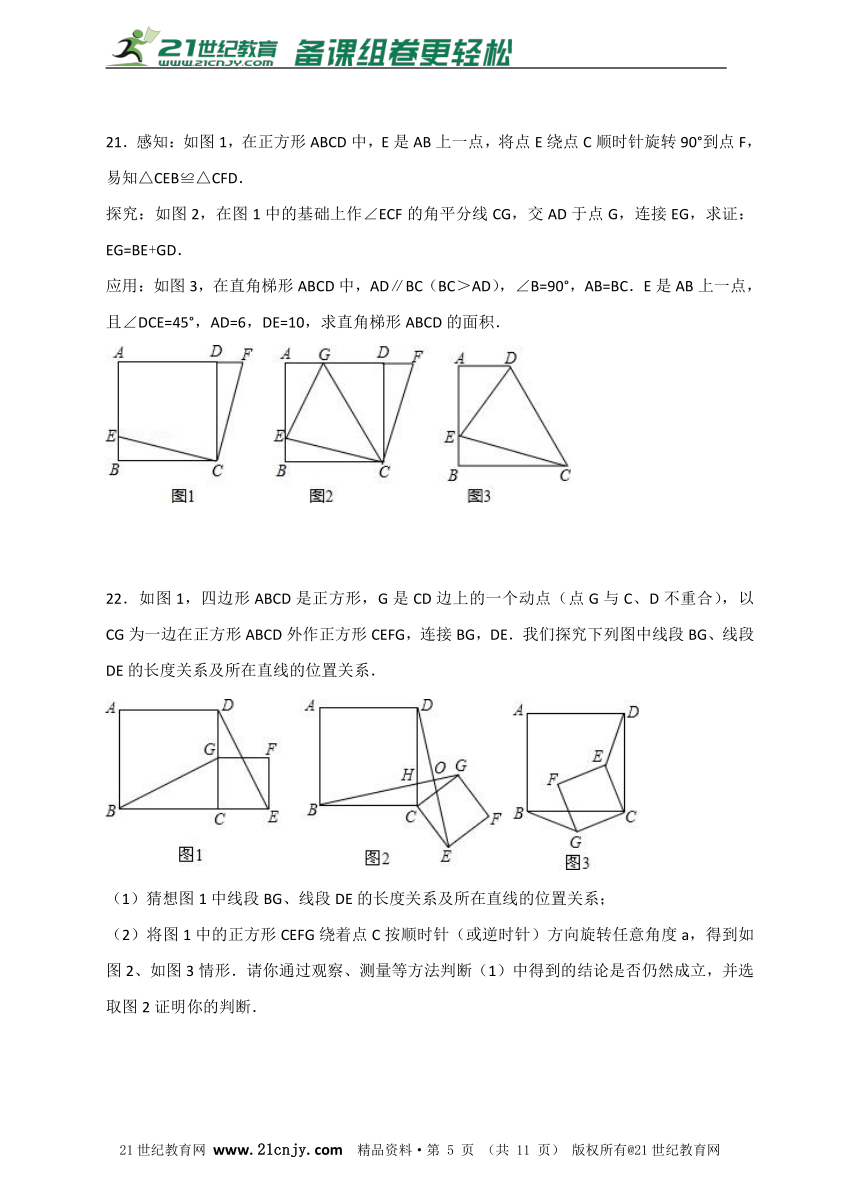
21．感知：如图1，在正方形ABCD中，E是AB上一点，将点E绕点C顺时针旋转90°到点F，易知△CEB≌△CFD．2·1·c·n·j·y
探究：如图2，在图1中的基础上作∠ECF的角平分线CG，交AD于点G，连接EG，求证：EG=BE+GD．21·世纪*教育网
应用：如图3，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B=90°，AB=BC．E是AB上一点，且∠DCE=45°，AD=6，DE=10，求直角梯形ABCD的面积．www-2-1-cnjy-com
22．如图1，四边形ABCD是正方形，G是CD边上的一个动点（点G与C、D不重合），以CG为一边在正方形ABCD外作正方形CEFG，连接BG，DE．我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系．2-1-c-n-j-y
（1）猜想图1中线段BG、线段DE的长度关系及所在直线的位置关系；
（2）将图1中的正方形CEFG绕着点C按顺时针（或逆时针）方向旋转任意角度a，得到如图2、如图3情形．请你通过观察、测量等方法判断（1）中得到的结论是否仍然成立，并选取图2证明你的判断．21*cnjy*com
　

浙教版八年级下数学第五章特殊平行四边形
参考答案与试题解析
一．选择题（共10小题）
2．解：（A）对角线相等是矩形具有的性质，菱形不一定具有；
（B）对角线互相平分是菱形和矩形共有的性质；
（C）对角线互相垂直是菱形具有的性质，矩形不一定具有；
（D）邻边互相垂直是矩形具有的性质，菱形不一定具有．故选：C．
3．解：∵四边形ABCD是正方形，∴∠CAB=∠BCA=45°；
△ACE中，AC=AE，则：∠ACE=∠AEC=（180°﹣∠CAE）=67.5°；
∴∠BCE=∠ACE﹣∠ACB=22.5°．故选A．
4．解：∵四边形ABCD菱形，
∴AC⊥BD，BD=2BO，
∵∠ABC=60°，
∴△ABC是正三角形，∴∠BAO=60°，∴BO=sin60°?AB=2×=，∴BD=2．
故选：D．
5．解：
∵四边形ABCD是菱形，∴AO=OC，BO=OD，AC⊥BD，
∵AC=8，DB=6，∴AO=4，OB=3，∠AOB=90°，
由勾股定理得：AB==5，
∵S菱形ABCD=，
∴，∴DH=，故选A．
6．解：∵E，F分别是AD，CD边上的中点，EF=，∴AC=2EF=2，
又∵BD=2，∴菱形ABCD的面积S=×AC×BD=×2×2=2，故选：A．
7．解：连接BF，
∵BC=6，点E为BC的中点，∴BE=3，
又∵AB=4，∴AE==5，∴BH=，则BF=，
∵FE=BE=EC，∴∠BFC=90°，∴CF==．故选：D．
8．解：如图连接AC，AD，分别交OB于G、P，作BK⊥OA于K．
∵四边形OABC是菱形，∴AC⊥OB，GC=AG，OG=BG=2，A、C关于直线OB对称，
∴PC+PD=PA+PD=DA，∴此时PC+PD最短，
在RT△AOG中，AG===，∴AC=2，
∵OA?BK=?AC?OB，∴BK=4，AK==3，∴点B坐标（8，4），
∴直线OB解析式为y=x，直线AD解析式为y=﹣x+1，
由解得，∴点P坐标（，）．故选D．
9．解：如图所示：∵四边形ABCD是正方形，
∴∠BAD=∠ABC=∠BCD=∠ADC=90°，AB=BC=CD=AD，∴∠BAE+∠DAG=90°，
在△ABE和△CDF中，，∴△ABE≌△CDF（SSS），∴∠ABE=∠CDF，
∵∠AEB=∠CFD=90°，∴∠ABE+∠BAE=90°，∴∠ABE=∠DAG=∠CDF，
同理：∠ABE=∠DAG=∠CDF=∠BCH，∴∠DAG+∠ADG=∠CDF+∠ADG=90°，
即∠DGA=90°，同理：∠CHB=90°，
10．解：∵四边形ABCD是矩形，
∴∠BAD=90°，OA=OC，OD=OB，AC=BD，∴OA=OD=OC=OB，
∵AE平分∠BAD，∴∠DAE=45°，
∵∠CAE=15°，∴∠DAC=30°，
∵OA=OD，∴∠ODA=∠DAC=30°，∴∠DOC=60°，
∵OD=OC，∴△ODC是等边三角形，∴①正确；
∵四边形ABCD是矩形，∴AD∥BC，∠ABC=90°∴∠DAC=∠ACB=30°，∴AC=2AB，
∵AC＞BC，∴2AB＞BC，∴②错误；
∵AD∥BC，∴∠DBC=∠ADB=30°，
∵AE平分∠DAB，∠DAB=90°，∴∠DAE=∠BAE=45°，
∵AD∥BC，∴∠DAE=∠AEB，∴∠AEB=∠BAE，∴AB=BE，
∵四边形ABCD是矩形，∴∠DOC=60°，DC=AB，
∵△DOC是等边三角形，∴DC=OD，∴BE=BO，∴∠BOE=∠BEO=（180°﹣∠OBE）=75°，
∵∠AOB=∠DOC=60°，∴∠AOE=60°+75°=135°，∴③正确；
∵OA=OC，∴根据等底等高的三角形面积相等得出S△AOE=SCOE，∴④正确；故选C．
二．填空题（共6小题）
11．解：∵正方形的边长为1cm，∴对角线长为=cm．故答案为cm．
12．解：∵四边形ABCD为菱形，∴AC⊥BD，AB=BC=CD=DA，∴△AOD为直角三角形．
∵OE=3，且点E为线段AD的中点，∴AD=2OE=6．C菱形ABCD=4AD=4×6=24．故答案为：24．
14．解：连接AC，
∵四边形ABCD是矩形，∴AD∥BE，AC=BD，且∠ADB=∠CAD=30°，∴∠E=∠DAE，
又∵BD=CE，∴CE=CA，∴∠E=∠CAE，
∵∠CAD=∠CAE+∠DAE，∴∠E+∠E=30°，即∠E=15°，
故答案为：15．
15．解：由勾股定理，得AB===8，
将五个小矩形的所有上边平移至AB，所有下边平移至CD，所有左边平移至AD，
所有右边平移至BC，
则五个小矩形的周长之和=2（AB+BC）=2×（6+8）=28．故答案为：28．
16．解：∵正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，
∴AB=BC=1，CE=EF=3，∠E=90°，
延长AD交EF于M，连接AC、CF，
则AM=BC+CE=1+3=4，FM=EF﹣AB=3﹣1=2，∠AMF=90°，
∵四边形ABCD和四边形GCEF是正方形，
∴∠ACD=∠GCF=45°，∴∠ACF=90°，
∵H为AF的中点，∴CH=AF，
在Rt△AMF中，由勾股定理得：AF===2，∴CH=，
故答案为：．
三．解答题（共6小题）
17．证明：∵四边形ABCD是正方形，∴AB=BC，∠ABE=∠BCF=90°，
∵∠AOF=90°，∠AOB=90°，∴∠BAE+∠OBA=90°，
又∵∠FBC+∠OBA=90°，∴∠BAE=∠CBF（同角的余角相等），
在△ABE和△BCF中∴，∴△ABE≌△BCF（ASA）．∴BE=CF．
19．（1）证明：∵△ABC与△CDE都是等边三角形∴AB=AC=BC，ED=DC=EC
∵点E、F分别为AC、BC的中点∴EF=AB，EC=AC，FC=BC∴EF=EC=FC∴EF=FC=ED=DC，
∴四边形EFCD是菱形．
（2）解：连接DF，与EC相交于点G，∵四边形EFCD是菱形∴DF⊥EC，垂足为G
∵EF=AB=4，EF∥AB∴∠FEG=∠A=60°
在Rt△EFG中，∠EGF=90°∴DF=2FG=2×4sin∠FEC=8sin60°=4．
20．（1）证明：∵CE∥BF，∴∠CED=∠BFD，∵D是BC边的中点，∴BD=DC，
在△BDF和△CDE中，∴△BDF≌△CDE（AAS）；
（2）四边形BFCE是矩形，
证明：∵△BDF≌△CDE，∴DE=DF，
∵BD=DC，∴四边形BFCE是平行四边形，
∵BD=CD，DE=BC，∴BD=DC=DE，∴∠BEC=90°，∴平行四边形BFCE是矩形．
应用：
解：如图3，过C作CH⊥AD于H，旋转△BCE到△CHM，则∠A=∠B=∠CHA=90°，
∵AB=BC，∴四边形ABCH是正方形，
∵∠DCE=45°，AH=BC，∴∠DCH+∠ECB=90°﹣45°=45°，
∵由已知证明知：△EBC≌△MHC，∴∠ECB=∠MCH，∴∠DCH+∠MCH=45°，
∴CD平分∠ECM，∴由探究证明知：DE=BE+DH，
在Rt△AED中，DE=10，AD=6，由勾股定理得：AE=8，
设BE=x，则BC=AB=x+8=AH，即x+8=6+10﹣x，x=4，BE=4，AB=4+8=12，BC=AB=12，
∴梯形ABCD的面积是×（6+12）×12=108．
　
22．解：（1）BG=DE，BG⊥DE；
∵四边形ABCD和四边形CEFG是正方形，
∴BC=DC，CG=CE，∠BCD=∠ECG=90°，∴∠BCG=∠DCE，
在△BCG和△DCE中， BC=DC∠BCG=∠DCE CG=CE，∴△BCG≌△DCE（SAS），∴BG=DE；
延长BG交DE于点H，
∵△BCG≌△DCE，∴∠CBG=∠CDE，
又∠CBG+∠BGC=90°，∴∠CDE+∠DGH=90°，∴∠DHG=90°，∴BH⊥DE，即BG⊥DE；