1.3 解直角三角形 同步练习(含答案)
文档属性
| 名称 | 1.3 解直角三角形 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 238.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-16 00:00:00 | ||
图片预览



文档简介
1.3
解直角三角形
同步练习
一、单选题
1、如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,cosA=,
则下列结论中正确的个数为(
)
①DE=3cm;②EB=1cm;③S菱形ABCD=15cm2
A、3个
B、2个
C、1个
D、0个
2、如图,在菱形ABCD中,∠ABC=60°,AC=4,则BD的长为(
)
A、2
B、4
C、8
D、8
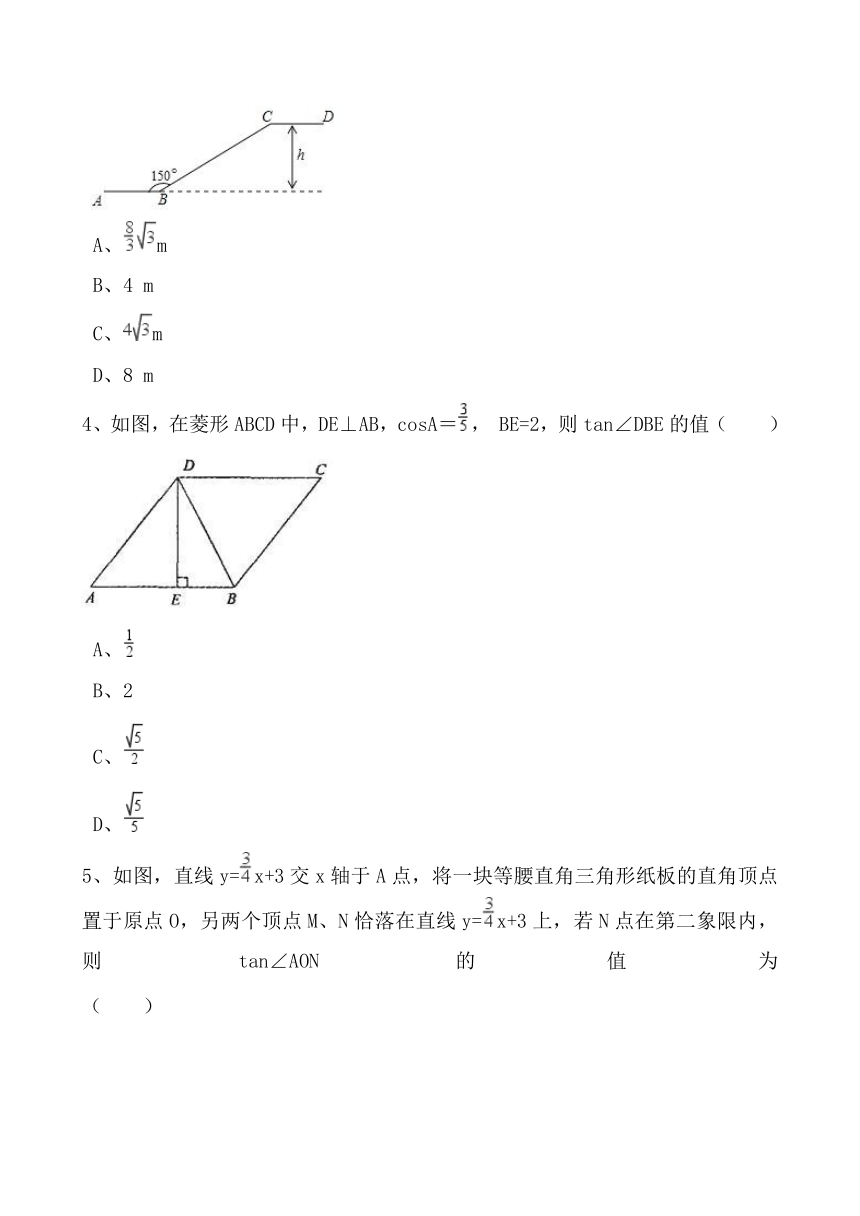
3、如图是某商场一楼与二楼之间的手扶电梯示意图.其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8
m,则乘电梯从点B到点C上升的高度h是(
)
A、m
B、4
m
C、m
D、8
m
4、如图,在菱形ABCD中,DE⊥AB,cosA=,
BE=2,则tan∠DBE的值( )
A、
B、2
C、
D、
5、如图,直线y=x+3交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰落在直线y=x+3上,若N点在第二象限内,则tan∠AON的值为( )
A、
B、
C、
D、
6、在等腰△ABC中,AB=AC=4,BC=6,那么cosB的值是
A、
B、
C、
D、
7、某水坝的坡度i=1:,
坡长AB=20米,则坝的高度为(
)
A、10米
B、20米
C、40米
D、20米
8、一斜坡长为米,高度为1米,那么坡比为( )
A、1:3
B、1:
C、1:
D、1:
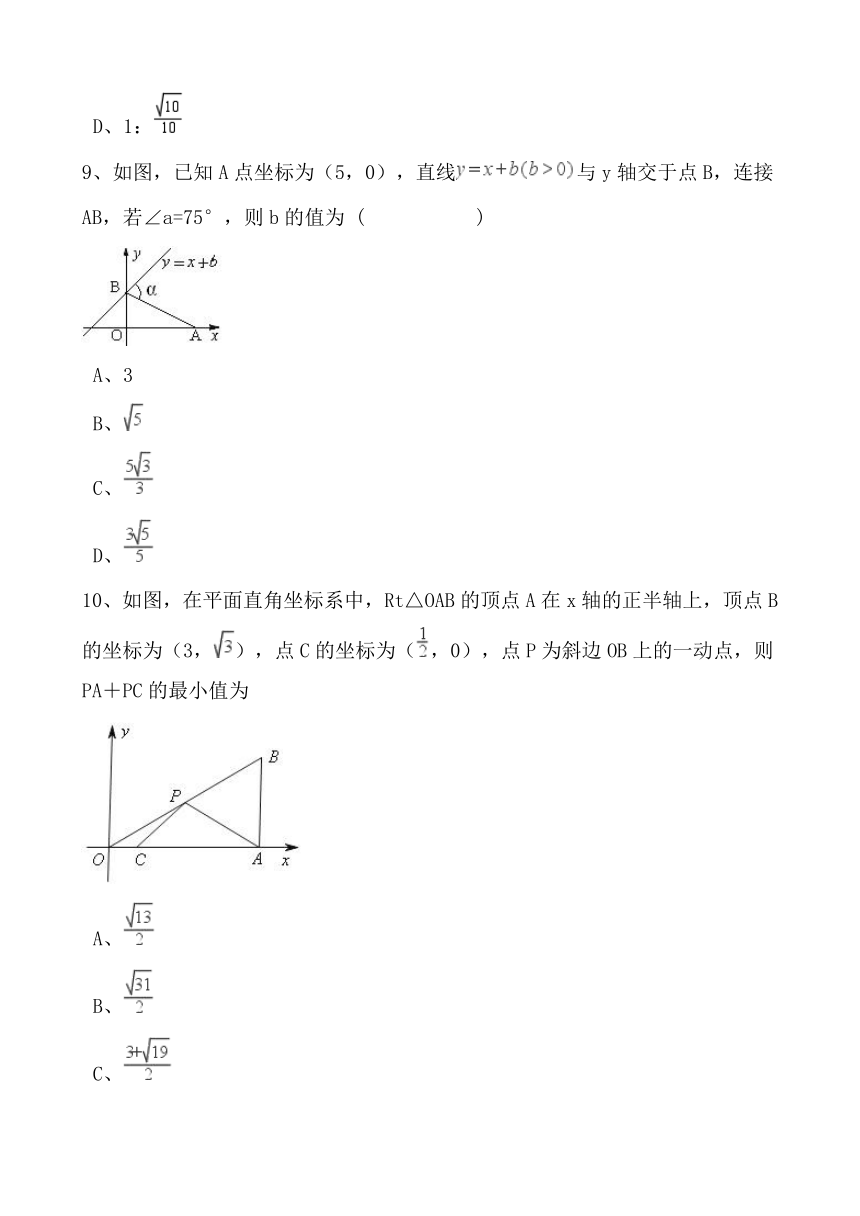
9、如图,已知A点坐标为(5,0),直线与y轴交于点B,连接AB,若∠a=75°,则b的值为
(
)
A、3
B、
C、
D、
10、如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,),点C的坐标为(,0),点P为斜边OB上的一动点,则PA+PC的最小值为
A、
B、
C、
D、2
11、在△ABC中,∠A,∠B均为锐角,且sinA=,
cosB=,
AC=40,则△ABC的面积是( )
A、800
B、800
C、400
D、400
12、如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为(
)
A、3
B、4
C、5
D、6
13、小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1米,则旗杆PA的高度为( )
A、
B、
C、
D、
14、一副三角板按图1所示的位置摆放.将△DEF绕点A(F)逆时针旋转60°后(图2),测得CG=10cm,则两个三角形重叠(阴影)部分的面积为(
)
A、75cm2
B、(25+25)cm2
C、(25+)cm2
D、(25+)cm2
15、如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′,若AC=1,则图中阴影部分的面积为( )
A、
B、
C、
D、3
二、填空题
16、在Rt△ABC中,∠A=90°,AB=2,若sinC=,
则BC的长度为________
17、已知∠AOB=60°,点P是∠AOB的平分线OC上的动点,点M在边OA上,且OM=4,则点P到点M与到边OA的距离之和的最小值是________.
18、如图,在平行四边形ABCD中,AD=5cm,
AP=8cm,
AP平分∠DAB,交DC于点P,过点B作BE⊥AD于点E,BE交AP于点F,则tan∠BFP=________
19、如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,
则CD=________
20、如图,在矩形ABCD中,AD=10,CD=6,E是CD边上一点,沿AE折叠△ADE,使点D恰好落在BC边上的F处,M是AF的中点,连接BM,则sin∠ABM=________.
三、解答题
21、如图,矩形ABCD的对角线AC.BD相交于点O
,
过点O作OE⊥AC交AD于E
,
若AB=6,AD=8,求sin∠OEA的值
.
22、如图的斜边AB=5,cosA=
(1)用尺规作图作线段AC的垂直平分线(保留作图痕迹,不要求写作法、证明);
(2)若直线与AB,AC分别相交于D,E两点,求DE的长
23、如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB
,
坡面AC的倾斜角为45°
.
为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=
:3
.
若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
≈1.414,
≈1.732)
24、如图,在△ABC中,∠ACB=90°,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
(1)求cos∠ADE的值;
(2)当DE=DC时,求AD的长.
25、如图,已知抛物线与x轴交于A、B两点,点C是抛物线在第一象限内部分的一个动点,点D是OC的中点,连接BD并延长,交AC于点E.
(1)说明:;
(2)当点C、点A到y轴距离相等时,求点E坐标.
(3)当的面积为时,求的值.
答案部分
一、单选题
1、
【答案】A
2、
【答案】B
3、
【答案】B
4、
【答案】B
5、
【答案】A
6、
【答案】C
7、
【答案】A
8、
【答案】A
9、
【答案】C
10、
【答案】B
11、
【答案】D
12、
【答案】B
13、
【答案】A
14、
【答案】C
15、
【答案】B
二、填空题
16、
【答案】10
17、
【答案】
18、
【答案】
19、
【答案】
20、
【答案】
三、解答题
21、
【答案】解:连接EC
,
∵四边形ABCD为矩形,
∴OA=OC
,
∠ABC=90°,
利用勾股定理得:AC=
=10,即OA=5,
∵OE⊥AC
,
∴AE=CE
,
在Rt△EDC中,设EC=AE=x
,
则有ED=AD-AE=8-x
,
DC=AB=6,
根据勾股定理得:x2=(8-x)2+62,
解得:x=
,
∴AE=
,
在Rt△AOE中,sin∠OEA=
.
22、
【答案】解:(1)作图
(2)因为直线垂直平分线段AC,所以CE=AE,
又因为BCAC,所以DE//BC,
所以DE=BC.
因为在中,AB=5,cosA=,
所以AC=ABcosA=,BC=4
得DE=2.
23、
【答案】解:需要拆除,理由为:
∵CB⊥AB
,
∠CAB=45°,
∴△ABC为等腰直角三角形,
∴AB=BC=10米,
在Rt△BCD中,新坡面DC的坡度为i=
:3,即∠CDB=30°,
∴DC=2BC=20米,BD=
米,
∴AD=BD-AB=(10
-10)米≈7.32米,
∵3+7.32=10.32>10,
∴需要拆除
.
24、
【答案】解:(1)∵DE⊥AB,
∴∠DEA=90°,
∴∠A+∠ADE=90°,
∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠ADE=∠B,
在Rt△ABC中,∵AC=12,BC=5,
∴AB=13,
∴,
∴;
(2)由(1)得,
设AD为x,则,
∵AC=AD+CD=12,
∴,
解得,
∴.
25、
【答案】解:(1)令y=0,则有-x2+2x+8=0.
解得:x1=-2,x2=4
∴OA=2,OB=4.
过点O作OG∥AC交BE于G
∴△CEG∽△OGD
∴
∵DC=DO
∴CE=0G
∵OG∥AC
∴△BOG∽△BAE
∴
∵OB=4,OA=2
∴;
(2)由(1)知A(-2,0),且点C、点A到y轴的距离相等,
∴C(2,8)
设AC所在直线解析式为:y=kx+b
把
A
、C两点坐标代入求得k=2,b=4
所以y=2x+4
分别过E、C作EF⊥x轴,CH⊥x轴,垂足分别为F、H
由△AEF∽△ACH可求EF=,OF=,
∴E点坐标为(,)
(3)连接OE
∵D是OC的中点,
∴S△OCE=2S△CED
∵S△OCE:S△AOC=CE:CA=2:5
∴S△CED:S△AOC=1:5.
∴S△AOC=5S△CED=8
∴
∴CH=8
解直角三角形
同步练习
一、单选题
1、如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,cosA=,
则下列结论中正确的个数为(
)
①DE=3cm;②EB=1cm;③S菱形ABCD=15cm2
A、3个
B、2个
C、1个
D、0个
2、如图,在菱形ABCD中,∠ABC=60°,AC=4,则BD的长为(
)
A、2
B、4
C、8
D、8
3、如图是某商场一楼与二楼之间的手扶电梯示意图.其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8
m,则乘电梯从点B到点C上升的高度h是(
)
A、m
B、4
m
C、m
D、8
m
4、如图,在菱形ABCD中,DE⊥AB,cosA=,
BE=2,则tan∠DBE的值( )
A、
B、2
C、
D、
5、如图,直线y=x+3交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M、N恰落在直线y=x+3上,若N点在第二象限内,则tan∠AON的值为( )
A、
B、
C、
D、
6、在等腰△ABC中,AB=AC=4,BC=6,那么cosB的值是
A、
B、
C、
D、
7、某水坝的坡度i=1:,
坡长AB=20米,则坝的高度为(
)
A、10米
B、20米
C、40米
D、20米
8、一斜坡长为米,高度为1米,那么坡比为( )
A、1:3
B、1:
C、1:
D、1:
9、如图,已知A点坐标为(5,0),直线与y轴交于点B,连接AB,若∠a=75°,则b的值为
(
)
A、3
B、
C、
D、
10、如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,),点C的坐标为(,0),点P为斜边OB上的一动点,则PA+PC的最小值为
A、
B、
C、
D、2
11、在△ABC中,∠A,∠B均为锐角,且sinA=,
cosB=,
AC=40,则△ABC的面积是( )
A、800
B、800
C、400
D、400
12、如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB、OC.若∠BAC与∠BOC互补,则弦BC的长为(
)
A、3
B、4
C、5
D、6
13、小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1米,则旗杆PA的高度为( )
A、
B、
C、
D、
14、一副三角板按图1所示的位置摆放.将△DEF绕点A(F)逆时针旋转60°后(图2),测得CG=10cm,则两个三角形重叠(阴影)部分的面积为(
)
A、75cm2
B、(25+25)cm2
C、(25+)cm2
D、(25+)cm2
15、如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′,若AC=1,则图中阴影部分的面积为( )
A、
B、
C、
D、3
二、填空题
16、在Rt△ABC中,∠A=90°,AB=2,若sinC=,
则BC的长度为________
17、已知∠AOB=60°,点P是∠AOB的平分线OC上的动点,点M在边OA上,且OM=4,则点P到点M与到边OA的距离之和的最小值是________.
18、如图,在平行四边形ABCD中,AD=5cm,
AP=8cm,
AP平分∠DAB,交DC于点P,过点B作BE⊥AD于点E,BE交AP于点F,则tan∠BFP=________
19、如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,
则CD=________
20、如图,在矩形ABCD中,AD=10,CD=6,E是CD边上一点,沿AE折叠△ADE,使点D恰好落在BC边上的F处,M是AF的中点,连接BM,则sin∠ABM=________.
三、解答题
21、如图,矩形ABCD的对角线AC.BD相交于点O
,
过点O作OE⊥AC交AD于E
,
若AB=6,AD=8,求sin∠OEA的值
.
22、如图的斜边AB=5,cosA=
(1)用尺规作图作线段AC的垂直平分线(保留作图痕迹,不要求写作法、证明);
(2)若直线与AB,AC分别相交于D,E两点,求DE的长
23、如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB
,
坡面AC的倾斜角为45°
.
为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=
:3
.
若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
≈1.414,
≈1.732)
24、如图,在△ABC中,∠ACB=90°,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
(1)求cos∠ADE的值;
(2)当DE=DC时,求AD的长.
25、如图,已知抛物线与x轴交于A、B两点,点C是抛物线在第一象限内部分的一个动点,点D是OC的中点,连接BD并延长,交AC于点E.
(1)说明:;
(2)当点C、点A到y轴距离相等时,求点E坐标.
(3)当的面积为时,求的值.
答案部分
一、单选题
1、
【答案】A
2、
【答案】B
3、
【答案】B
4、
【答案】B
5、
【答案】A
6、
【答案】C
7、
【答案】A
8、
【答案】A
9、
【答案】C
10、
【答案】B
11、
【答案】D
12、
【答案】B
13、
【答案】A
14、
【答案】C
15、
【答案】B
二、填空题
16、
【答案】10
17、
【答案】
18、
【答案】
19、
【答案】
20、
【答案】
三、解答题
21、
【答案】解:连接EC
,
∵四边形ABCD为矩形,
∴OA=OC
,
∠ABC=90°,
利用勾股定理得:AC=
=10,即OA=5,
∵OE⊥AC
,
∴AE=CE
,
在Rt△EDC中,设EC=AE=x
,
则有ED=AD-AE=8-x
,
DC=AB=6,
根据勾股定理得:x2=(8-x)2+62,
解得:x=
,
∴AE=
,
在Rt△AOE中,sin∠OEA=
.
22、
【答案】解:(1)作图
(2)因为直线垂直平分线段AC,所以CE=AE,
又因为BCAC,所以DE//BC,
所以DE=BC.
因为在中,AB=5,cosA=,
所以AC=ABcosA=,BC=4
得DE=2.
23、
【答案】解:需要拆除,理由为:
∵CB⊥AB
,
∠CAB=45°,
∴△ABC为等腰直角三角形,
∴AB=BC=10米,
在Rt△BCD中,新坡面DC的坡度为i=
:3,即∠CDB=30°,
∴DC=2BC=20米,BD=
米,
∴AD=BD-AB=(10
-10)米≈7.32米,
∵3+7.32=10.32>10,
∴需要拆除
.
24、
【答案】解:(1)∵DE⊥AB,
∴∠DEA=90°,
∴∠A+∠ADE=90°,
∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠ADE=∠B,
在Rt△ABC中,∵AC=12,BC=5,
∴AB=13,
∴,
∴;
(2)由(1)得,
设AD为x,则,
∵AC=AD+CD=12,
∴,
解得,
∴.
25、
【答案】解:(1)令y=0,则有-x2+2x+8=0.
解得:x1=-2,x2=4
∴OA=2,OB=4.
过点O作OG∥AC交BE于G
∴△CEG∽△OGD
∴
∵DC=DO
∴CE=0G
∵OG∥AC
∴△BOG∽△BAE
∴
∵OB=4,OA=2
∴;
(2)由(1)知A(-2,0),且点C、点A到y轴的距离相等,
∴C(2,8)
设AC所在直线解析式为:y=kx+b
把
A
、C两点坐标代入求得k=2,b=4
所以y=2x+4
分别过E、C作EF⊥x轴,CH⊥x轴,垂足分别为F、H
由△AEF∽△ACH可求EF=,OF=,
∴E点坐标为(,)
(3)连接OE
∵D是OC的中点,
∴S△OCE=2S△CED
∵S△OCE:S△AOC=CE:CA=2:5
∴S△CED:S△AOC=1:5.
∴S△AOC=5S△CED=8
∴
∴CH=8
