2.3 三角形的内切圆 同步练习(含答案)
文档属性
| 名称 | 2.3 三角形的内切圆 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 337.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-16 12:52:34 | ||
图片预览




文档简介
2.3
三角形的内切圆
同步练习
一、单选题
1、下列说法:
①平分弦的直径垂直于弦;②三点确定一个圆;③相等的圆心角所对的弧相等;④垂直于半径的直线是圆的切线;⑤三角形的内心到三条边的距离相等。
其中不正确的有( )个。
A、1
B、2
C、3
D、4
2、如图,直线a、b、c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有(
)
A、一处
B、两处
C、三处
D、四处
3、在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分别为( )
A、1.5,2.5
B、2,5
C、1,2.5
D、2,2.5
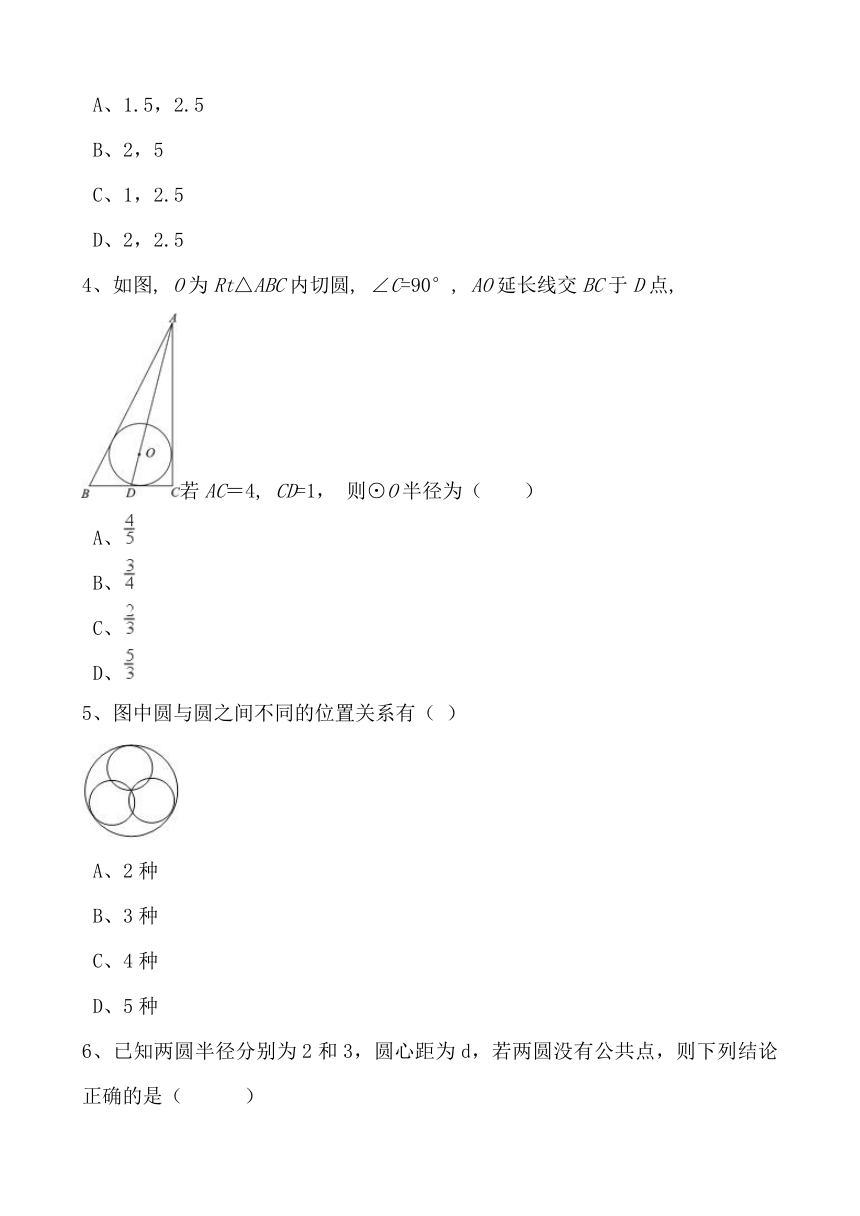
4、如图,
O为Rt△ABC内切圆,
∠C=90°,
AO延长线交BC于D点,
若AC=4,
CD=1,
则⊙O半径为( )
A、
B、
C、
D、
5、图中圆与圆之间不同的位置关系有(
)
A、2种
B、3种
C、4种
D、5种
6、已知两圆半径分别为2和3,圆心距为d,若两圆没有公共点,则下列结论正确的是(
)
A、0<d<1
B、d>5
C、0<d<1或d>5
D、0≤d<1或d>5
7、在△ABC中,已知∠C=90°,BC=3,AC=4,则它的内切圆半径是
(
)
A、
B、1
C、2
D、
8、如图4,国际奥委会会旗上的图案是由五个圆环组成,在这个图案中反映出的两圆位置关系有( )
A、内切、相交
B、外离、相交
C、外切、外离
D、外离、内切
9、若⊙O1
,
⊙O2的半径分别是r1=5,r2=3,圆心距d=8,则这两个圆的位置关系是( )
A、内切
B、相交
C、外切
D、外离
10、⊙O1和⊙O2的半径分别为3cm和5cm,若O1O2=8cm,则⊙O1和⊙O2的位置关系是
A、外切
B、相交
C、内切
D、内含
11、两圆的半径分别为R和r,圆心距d=3,且R、r是方程的两个根,则这两个圆的位置关系是( )
A、内切
B、外切
C、相交
D、内含
12、在△ABC中,O为内心,∠A=80°,则∠BOC=( )
A、140°
B、135°
C、130°
D、125°
13、如图,△ABC中,下面说法正确的个数是( )个.
①若O是△ABC的外心,∠A=50°,则∠BOC=100°;
②若O是△ABC的内心,∠A=50°,则∠BOC=115°;
③若BC=6,AB+AC=10,则△ABC的面积的最大值是12;
④△ABC的面积是12,周长是16,则其内切圆的半径是1.
A、1
B、2
C、3
D、4
二、填空题
14、若直角三角形的两条直角边长分别是6和8,则它的外接圆半径为________ ,内切圆半径为________ .
15、在Rt△ABC中,∠C=90°,BC=5cm,AC=12cm,⊙O是Rt△ABC的内切圆,则⊙O的面积是 ________(用含π的式子表示).
16、如图,在△ABC中,已知∠C=90°,BC=6,AC=8,则它的内切圆半径是________
17、如图,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O切AB,BC,AC于点D,E,F,则AF的长为________.
18、如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:
①∠BOC=90 +∠A;
②以E为圆心、BE为半径的圆与以F为圆心、CF为半径的圆外切;③设OD=m,AE+AF=n,则S△AEF=mn;
④EF是△ABC的中位线.其中正确的结论是________.
三、解答题
19、如图,△ABC的周长为24,面积为24,求它的内切圆的半径.
20、如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P是边AC上的一动点,PH⊥AB,垂足为H.
(1)求⊙O的半径的长及线段AD的长;
(2)设PH=x,PC=y,求y关于x的函数关系式.
21、△ABC的内切圆⊙O与BC,CA,AB分别相切于点D、E、F,且AB=11cm,BC=16cm,CA=15cm,求AF、BD、CE的长?
22、在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.如图,⊙O是△ABC的内切圆,与三边分别相切于点E、F、G.
(1)求证:内切圆的半径r=1;
(2)求tan∠OAG的值.
23、如图△ABC内接于圆O,I是△ABC的内心,AI的延长线交圆O于点D.
(1)求证:BD=DI;
(2)若OI⊥AD,求的值.
24、已知:如图,点N为△ABC的内心,延长AN交BC于点D,交△ABC的外接圆于点E.
(1)求证:EB=EN=EC;
(2)求证:NE2=AE DE.
25、如图,⊙O的内接四边形ABCD中,AC,BD是它的对角线,AC的中点I是△ABD的内心.求证:
(1)OI是△IBD的外接圆的切线;
(2)AB+AD=2BD.
答案部分
一、单选题
1、
【答案】D
2、
【答案】D
3、
【答案】C
4、
【答案】A
5、
【答案】A
6、
【答案】D
7、
【答案】B
8、
【答案】B
9、
【答案】C
10、
【答案】A
11、
【答案】A
12、
【答案】C
13、
【答案】C
二、填空题
14、
【答案】5;2
15、
【答案】4πcm2
16、
【答案】2
17、
【答案】4.5
18、
【答案】①②
三、解答题
19、
【答案】解:连结OA、OB、OC,作OD⊥AB于D,OE⊥BC于E,OF⊥AC于F,
设它的内切圆的半径为r,则OD=OE=OF=r,
∵S△ABC=S△AOB+S△OBC+S△OAC
,
∴ r AB+ r BC+ r AC=24,
∴r(AB+BC+AC)=24,
∴r 24=24,
∴r=2.
即它的内切圆的半径为2.
20、
【答案】解:(1)连接AO、DO.设⊙O的半径为r.
在Rt△ABC中,由勾股定理得AC==4,
则⊙O的半径r=(AC+BC﹣AB)=(4+3﹣5)=1;
∵CE、CF是⊙O的切线,∠ACB=90°,
∴∠CFO=∠FCE=∠CEO=90°,CF=CE,
∴四边形CEOF是正方形,
∴CF=OF=1;
又∵AD、AF是⊙O的切线,
∴AF=AD;
∴AF=AC﹣CF=AC﹣OF=4﹣1=3,
即AD=3;
(2)点P在线段AC上时.
在Rt△ABC中,AB=5,AC=4,BC=3,
∵∠C=90°,PH⊥AB,
∴∠C=∠PHA=90°,
∵∠A=∠A,
∴△AHP∽△ACB,
∴,
即
∴y=﹣x+4,
即y与x的函数关系式是y=﹣x+4.
21、
【答案】解:∵△ABC的内切圆⊙O与BC,CA,AB分别相切于点D、E、F,
∴AF=AE,BF=BD,CD=CE.
设AF=AE=x,则BF=BD=11﹣x,EC=DC=15﹣x.
根据题意得11﹣x+15﹣x=16.
解得;x=5cm.
∴AF=5cm.BD=11﹣x=11﹣5=6cm,EC=15﹣x=10cm.
∴AF=5cm,BD=6cm,EC=10cm.
22、
【答案】(1)证明:如图连结OE,OF,OG.
∵⊙O是△ABC的内切圆,∠C=90°,
∴四边形CEOF是正方形,
∴CE=CF=r.
又∵AG=AE=3﹣r,BG=BF=4﹣r,AG+BG=5,
∴(3﹣r)+(4﹣r)=5.
解得r=1;
(2)解:连结OA,在Rt△AOG中,
∵r=1,AG=3﹣r=2,
tan∠OAG=.
23、
【答案】(1)证明:∵点I是△ABC的内心
∴∠BAD=∠CAD,∠ABI=∠CBI
∵∠CBD=∠CAD
∴∠BAD=∠CBD
∴∠BID=∠ABI+∠BAD,∠BAD=∠CAD=∠CBD,
∵∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD
∴ID=BD;
(2)解:连接OA、OD、BD和BI,
∵OA=OD,OI⊥AD
∴AI=ID,
∵I为△ABC内心,
∴∠BAD=∠BCD,
∴弧BD=弧CD,
∵弧CD=弧CD,
∴∠BCD=∠BAD,
∴∠DBI=∠BCD+∠CBI=∠CAD+∠CBI,
=(∠BAC+∠ACB),
∵∠DIB=∠DAB+∠ABI=(∠BAC+∠ABC),
∴∠DIB=∠DBI,
∴BD=ID=AI,,
故OD⊥BC,记垂足为E,则有BE=BC,
作IG⊥AB于G,又∠DBE=∠IAG,而BD=AI,
∴Rt△BDE≌Rt△AIG,
于是,AG=BE=BC,但AG=(AB+AC﹣BC),
故AB+AC=2BC,
∴=2.
24、
【答案】证明:(1)连接BN,
∵点N为△ABC的内心,
∴∠1=∠2,∠3=∠4.
∴∠BCE=∠1,
∴EB=EC.
∵∠5与∠2都是弧EC所对的圆周角,
∴∠5=∠2=∠1.
∴∠4+∠5=∠3+∠1.
∵∠NBE=∠4+∠5,∠BNE=∠3+∠1,
∴∠NBE=∠BNE.
∴EB=EN.
∴EB=EN=EC.
(2)由(1)知∠5=∠2=∠1,∠BED=∠AEB,
∴△BED∽△AEB.
∴.
即BE2=AE DE.
∵EB=EN,
∴NE2=AE DE.
25、
【答案】解:(1)∵∠CID=∠IAD+∠IDA,∠CDI=∠CDB+∠BDI=∠BAC+∠IDA=∠IAD+∠IDA
∴∠CID=∠CDI,
∴CI=CD.
同理,CI=CB.
故点C是△IBD的外心.
连接OA,OC,
∵I是AC的中点,且OA=OC,
∴OI⊥AC,即OI⊥CI.
∴OI是△IBD外接圆的切线.
(2)由(1)可得:
∵AC的中点I是△ABD的内心,
∴∠BAC=∠CAD
∴∠BDC=∠DAC=∠BAC,
又∵∠ACD=∠DCF,
∴△ADC∽△DFC,
∴,
∵AC=2CI
∴AC=2CD
∴AD=2DF
同理可得:AB=2BF
∴AB+AD=2BF+2DF=2BD.
三角形的内切圆
同步练习
一、单选题
1、下列说法:
①平分弦的直径垂直于弦;②三点确定一个圆;③相等的圆心角所对的弧相等;④垂直于半径的直线是圆的切线;⑤三角形的内心到三条边的距离相等。
其中不正确的有( )个。
A、1
B、2
C、3
D、4
2、如图,直线a、b、c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有(
)
A、一处
B、两处
C、三处
D、四处
3、在Rt△ABC中,∠C=90°,AC=3,AB=5,则它的内切圆与外接圆半径分别为( )
A、1.5,2.5
B、2,5
C、1,2.5
D、2,2.5
4、如图,
O为Rt△ABC内切圆,
∠C=90°,
AO延长线交BC于D点,
若AC=4,
CD=1,
则⊙O半径为( )
A、
B、
C、
D、
5、图中圆与圆之间不同的位置关系有(
)
A、2种
B、3种
C、4种
D、5种
6、已知两圆半径分别为2和3,圆心距为d,若两圆没有公共点,则下列结论正确的是(
)
A、0<d<1
B、d>5
C、0<d<1或d>5
D、0≤d<1或d>5
7、在△ABC中,已知∠C=90°,BC=3,AC=4,则它的内切圆半径是
(
)
A、
B、1
C、2
D、
8、如图4,国际奥委会会旗上的图案是由五个圆环组成,在这个图案中反映出的两圆位置关系有( )
A、内切、相交
B、外离、相交
C、外切、外离
D、外离、内切
9、若⊙O1
,
⊙O2的半径分别是r1=5,r2=3,圆心距d=8,则这两个圆的位置关系是( )
A、内切
B、相交
C、外切
D、外离
10、⊙O1和⊙O2的半径分别为3cm和5cm,若O1O2=8cm,则⊙O1和⊙O2的位置关系是
A、外切
B、相交
C、内切
D、内含
11、两圆的半径分别为R和r,圆心距d=3,且R、r是方程的两个根,则这两个圆的位置关系是( )
A、内切
B、外切
C、相交
D、内含
12、在△ABC中,O为内心,∠A=80°,则∠BOC=( )
A、140°
B、135°
C、130°
D、125°
13、如图,△ABC中,下面说法正确的个数是( )个.
①若O是△ABC的外心,∠A=50°,则∠BOC=100°;
②若O是△ABC的内心,∠A=50°,则∠BOC=115°;
③若BC=6,AB+AC=10,则△ABC的面积的最大值是12;
④△ABC的面积是12,周长是16,则其内切圆的半径是1.
A、1
B、2
C、3
D、4
二、填空题
14、若直角三角形的两条直角边长分别是6和8,则它的外接圆半径为________ ,内切圆半径为________ .
15、在Rt△ABC中,∠C=90°,BC=5cm,AC=12cm,⊙O是Rt△ABC的内切圆,则⊙O的面积是 ________(用含π的式子表示).
16、如图,在△ABC中,已知∠C=90°,BC=6,AC=8,则它的内切圆半径是________
17、如图,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆⊙O切AB,BC,AC于点D,E,F,则AF的长为________.
18、如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:
①∠BOC=90 +∠A;
②以E为圆心、BE为半径的圆与以F为圆心、CF为半径的圆外切;③设OD=m,AE+AF=n,则S△AEF=mn;
④EF是△ABC的中位线.其中正确的结论是________.
三、解答题
19、如图,△ABC的周长为24,面积为24,求它的内切圆的半径.
20、如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P是边AC上的一动点,PH⊥AB,垂足为H.
(1)求⊙O的半径的长及线段AD的长;
(2)设PH=x,PC=y,求y关于x的函数关系式.
21、△ABC的内切圆⊙O与BC,CA,AB分别相切于点D、E、F,且AB=11cm,BC=16cm,CA=15cm,求AF、BD、CE的长?
22、在Rt△ABC中,∠C=90°,AC=3,BC=4,AB=5.如图,⊙O是△ABC的内切圆,与三边分别相切于点E、F、G.
(1)求证:内切圆的半径r=1;
(2)求tan∠OAG的值.
23、如图△ABC内接于圆O,I是△ABC的内心,AI的延长线交圆O于点D.
(1)求证:BD=DI;
(2)若OI⊥AD,求的值.
24、已知:如图,点N为△ABC的内心,延长AN交BC于点D,交△ABC的外接圆于点E.
(1)求证:EB=EN=EC;
(2)求证:NE2=AE DE.
25、如图,⊙O的内接四边形ABCD中,AC,BD是它的对角线,AC的中点I是△ABD的内心.求证:
(1)OI是△IBD的外接圆的切线;
(2)AB+AD=2BD.
答案部分
一、单选题
1、
【答案】D
2、
【答案】D
3、
【答案】C
4、
【答案】A
5、
【答案】A
6、
【答案】D
7、
【答案】B
8、
【答案】B
9、
【答案】C
10、
【答案】A
11、
【答案】A
12、
【答案】C
13、
【答案】C
二、填空题
14、
【答案】5;2
15、
【答案】4πcm2
16、
【答案】2
17、
【答案】4.5
18、
【答案】①②
三、解答题
19、
【答案】解:连结OA、OB、OC,作OD⊥AB于D,OE⊥BC于E,OF⊥AC于F,
设它的内切圆的半径为r,则OD=OE=OF=r,
∵S△ABC=S△AOB+S△OBC+S△OAC
,
∴ r AB+ r BC+ r AC=24,
∴r(AB+BC+AC)=24,
∴r 24=24,
∴r=2.
即它的内切圆的半径为2.
20、
【答案】解:(1)连接AO、DO.设⊙O的半径为r.
在Rt△ABC中,由勾股定理得AC==4,
则⊙O的半径r=(AC+BC﹣AB)=(4+3﹣5)=1;
∵CE、CF是⊙O的切线,∠ACB=90°,
∴∠CFO=∠FCE=∠CEO=90°,CF=CE,
∴四边形CEOF是正方形,
∴CF=OF=1;
又∵AD、AF是⊙O的切线,
∴AF=AD;
∴AF=AC﹣CF=AC﹣OF=4﹣1=3,
即AD=3;
(2)点P在线段AC上时.
在Rt△ABC中,AB=5,AC=4,BC=3,
∵∠C=90°,PH⊥AB,
∴∠C=∠PHA=90°,
∵∠A=∠A,
∴△AHP∽△ACB,
∴,
即
∴y=﹣x+4,
即y与x的函数关系式是y=﹣x+4.
21、
【答案】解:∵△ABC的内切圆⊙O与BC,CA,AB分别相切于点D、E、F,
∴AF=AE,BF=BD,CD=CE.
设AF=AE=x,则BF=BD=11﹣x,EC=DC=15﹣x.
根据题意得11﹣x+15﹣x=16.
解得;x=5cm.
∴AF=5cm.BD=11﹣x=11﹣5=6cm,EC=15﹣x=10cm.
∴AF=5cm,BD=6cm,EC=10cm.
22、
【答案】(1)证明:如图连结OE,OF,OG.
∵⊙O是△ABC的内切圆,∠C=90°,
∴四边形CEOF是正方形,
∴CE=CF=r.
又∵AG=AE=3﹣r,BG=BF=4﹣r,AG+BG=5,
∴(3﹣r)+(4﹣r)=5.
解得r=1;
(2)解:连结OA,在Rt△AOG中,
∵r=1,AG=3﹣r=2,
tan∠OAG=.
23、
【答案】(1)证明:∵点I是△ABC的内心
∴∠BAD=∠CAD,∠ABI=∠CBI
∵∠CBD=∠CAD
∴∠BAD=∠CBD
∴∠BID=∠ABI+∠BAD,∠BAD=∠CAD=∠CBD,
∵∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD
∴ID=BD;
(2)解:连接OA、OD、BD和BI,
∵OA=OD,OI⊥AD
∴AI=ID,
∵I为△ABC内心,
∴∠BAD=∠BCD,
∴弧BD=弧CD,
∵弧CD=弧CD,
∴∠BCD=∠BAD,
∴∠DBI=∠BCD+∠CBI=∠CAD+∠CBI,
=(∠BAC+∠ACB),
∵∠DIB=∠DAB+∠ABI=(∠BAC+∠ABC),
∴∠DIB=∠DBI,
∴BD=ID=AI,,
故OD⊥BC,记垂足为E,则有BE=BC,
作IG⊥AB于G,又∠DBE=∠IAG,而BD=AI,
∴Rt△BDE≌Rt△AIG,
于是,AG=BE=BC,但AG=(AB+AC﹣BC),
故AB+AC=2BC,
∴=2.
24、
【答案】证明:(1)连接BN,
∵点N为△ABC的内心,
∴∠1=∠2,∠3=∠4.
∴∠BCE=∠1,
∴EB=EC.
∵∠5与∠2都是弧EC所对的圆周角,
∴∠5=∠2=∠1.
∴∠4+∠5=∠3+∠1.
∵∠NBE=∠4+∠5,∠BNE=∠3+∠1,
∴∠NBE=∠BNE.
∴EB=EN.
∴EB=EN=EC.
(2)由(1)知∠5=∠2=∠1,∠BED=∠AEB,
∴△BED∽△AEB.
∴.
即BE2=AE DE.
∵EB=EN,
∴NE2=AE DE.
25、
【答案】解:(1)∵∠CID=∠IAD+∠IDA,∠CDI=∠CDB+∠BDI=∠BAC+∠IDA=∠IAD+∠IDA
∴∠CID=∠CDI,
∴CI=CD.
同理,CI=CB.
故点C是△IBD的外心.
连接OA,OC,
∵I是AC的中点,且OA=OC,
∴OI⊥AC,即OI⊥CI.
∴OI是△IBD外接圆的切线.
(2)由(1)可得:
∵AC的中点I是△ABD的内心,
∴∠BAC=∠CAD
∴∠BDC=∠DAC=∠BAC,
又∵∠ACD=∠DCF,
∴△ADC∽△DFC,
∴,
∵AC=2CI
∴AC=2CD
∴AD=2DF
同理可得:AB=2BF
∴AB+AD=2BF+2DF=2BD.
