1.1 锐角三角函数 同步练习(含答案)
文档属性
| 名称 | 1.1 锐角三角函数 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 254.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-02-16 12:51:03 | ||
图片预览



文档简介
1.1
锐角三角函数
同步练习
一、单选题
1、如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①tan∠AEC=;②S△ABC+S△CDE≥S△ACE;③BM⊥DM;④BM=DM.正确结论的个数是( )
A、1个
B、2个
C、3个
D、4个
2、在△ABC中,∠C=90°,AB=6,BC=2,则下列三角函数表示正确的是( )
A、sinA=
B、cosB=2
C、tanA=
D、cosA=
3、已知α是锐角,cosα=,
则tanα的值是( )
A、
B、
C、3
D、
4、如果α是锐角,且cosα=,那么sinα的值是(
)
A、
B、
C、
D、
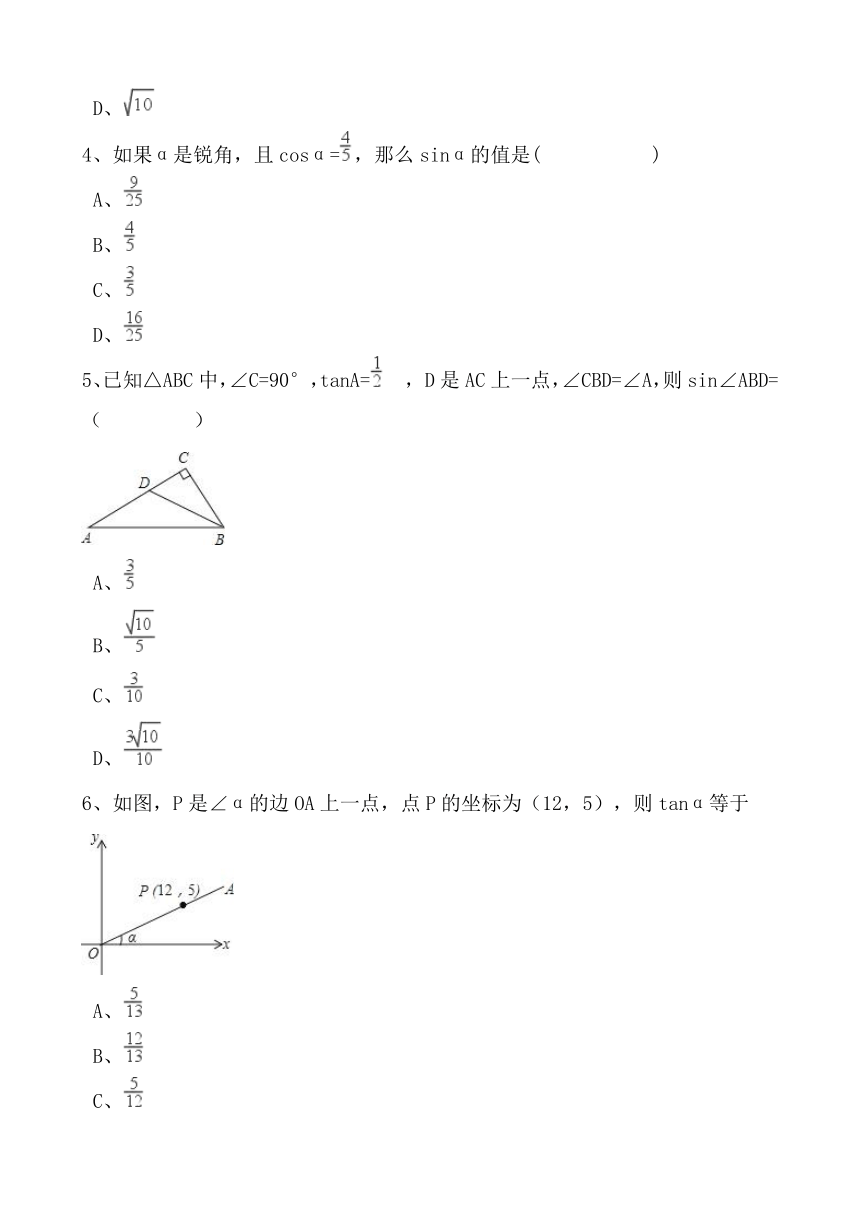
5、已知△ABC中,∠C=90°,tanA=
,
D是AC上一点,∠CBD=∠A,则sin∠ABD=(
)
A、
B、
C、
D、
6、如图,P是∠α的边OA上一点,点P的坐标为(12,5),则tanα等于
A、
B、
C、
D、
7、Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,且a:b=3:4,斜边c=15,则b的值是( )
A、12
B、9
C、4
D、3
8、如图,已知⊙O的半径为5,AB=8,
锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )
A、
B、
C、
D、
9、如图,在□ABCD中,AB∶AD=3∶2,∠ADB=60°,那么cosA的值等于( )
A、
B、
C、
D、
10、已知α、β都是锐角,如果sinα=cosβ,那么α与β之间满足的关系是( )
A、α=β;
B、α+β=90°;
C、α-β=90°;
D、β-α=90°.
11、已知α为锐角,则m=sin2α+cos2α的值( )
A、m>1
B、m=1
C、m<1
D、m≥1
12、图1,在Rt△ABC中,∠ACB=90°,点P以每秒1cm的速度从点A出发,沿折线AC-CB运动,到点B停止,过点P作PD⊥AB,垂足为D,PD的长y(cm)与点P的运动时间x(秒)的函数图象如图2所示,当点P运动5秒时,PD的长是(
)
A、1.5cm
B、1.2cm
C、1.8cm
D、2cm
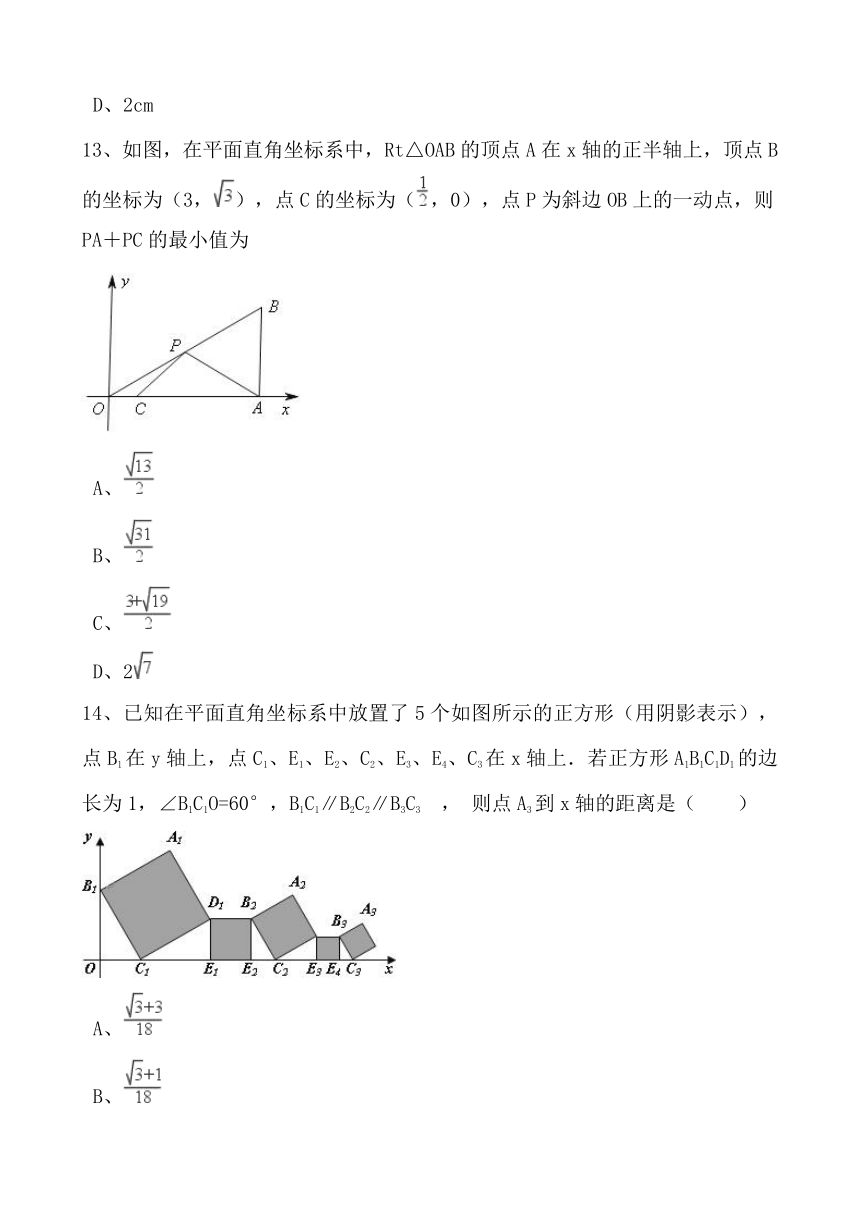
13、如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,),点C的坐标为(,0),点P为斜边OB上的一动点,则PA+PC的最小值为
A、
B、
C、
D、2
14、已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3在x轴上.若正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3
,
则点A3到x轴的距离是( )
A、
B、
C、
D、
二、填空题
15、求值:________
16、已知α是锐角且tanα=,
则sinα+cosα=________
17、在Rt△ABC中,∠C=90°,sin∠A=,
则tan∠B的值为________
18、已知α、β均为锐角,且满足|sinα﹣|+=0,则α+β= ________.
19、如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30o得到正方形AB′C′D′,则它们的公共部分的面积等于________
。
三、计算题
20、计算:
21、
(1)计算:
4cos245°-|-2|
+
tan45°;
(2)分解因式:
四、解答题
22、已知tanα=,
α是锐角,求tan(9O°﹣α),sinα,cosα的值.
23、已知[4(xy﹣1)2﹣(xy+2)(2﹣xy)]÷xy,其中x=(﹣cos60°)﹣1
,
y=﹣sin30°.
24、如图,点C在⊙O的直径BA的延长线上,AB=2AC,CD切⊙O于点D,连接CD,OD.
(1)求角C的正切值:
(2)若⊙O的半径r=2,求BD的长度.
25、如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE=,A(3,0),D(﹣1,0),E(0,3).
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由;
(4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE与△ABE重叠部分的面积为s,求s与t之间的函数关系式,并指出t的取值范围.
答案部分
一、单选题
1、
【答案】D
2、
【答案】C
3、
【答案】B
4、
【答案】C
5、
【答案】A
6、
【答案】C
7、
【答案】A
8、
【答案】A
9、
【答案】A
10、
【答案】B
11、
【答案】B
12、
【答案】B
13、
【答案】B
14、
【答案】D
二、填空题
15、
【答案】
16、
【答案】
17、
【答案】
18、
【答案】75°
19、
【答案】
三、计算题
20、
【答案】解:原式==9+8+1-3=15.
21、
【答案】解:(1)
4cos245°-|-2|
+
tan45°
=4x-2+1
=4x-1
=2-1
=1
(2)分解因式:
=a(-9)
=a(a-3)(a+3)
四、解答题
22、
【答案】解:∵如图所示:tanB=tanα=,
∴设AC=2x,BC=5x,则AB=x,
∴tan(9O°﹣α)==,
sinα===,
cosα===.
23、
【答案】解:∵x=(﹣cos60°)﹣1=(﹣)﹣1=﹣2,y=﹣sin30°=﹣,
∴[4(xy﹣1)2﹣(xy+2)(2﹣xy)]÷xy
=[4(x2y2﹣2xy+1)﹣(22﹣x2y2)]
=(4x2y2﹣8xy+4﹣4+x2y2)
=(5x2y2﹣8xy)
=20xy﹣32
=20×(﹣2)×(﹣)﹣32
=﹣12.
24、
【答案】解:(1)∵CD切⊙O于点D,
∴CD⊥OD,
又∵AB=2AC,
∴OD=AO=AC=CO
∴∠C=30°
∴tan∠C=;
(2)连接AD,
∵AB是直径,
∴∠ADB=90°,
∵∠DOA=90°﹣30°=60°,
又∵OD=OA,
∴△DAO是等边三角形.
∴DA=r=2,
∴DB==.
25、
【答案】(1)解:由题意,设抛物线解析式为y=a(x﹣3)(x+1).
将E(0,3)代入上式,解得:a=﹣1.
∴y=﹣x2+2x+3.
则点B(1,4).
(2)证明:如图1,过点B作BM⊥y于点M,则M(0,4).
在Rt△AOE中,OA=OE=3,
∴∠1=∠2=45°,AE==3.
在Rt△EMB中,EM=OM﹣OE=1=BM,
∴∠MEB=∠MBE=45°,BE==.
∴∠BEA=180°﹣∠1﹣∠MEB=90°.
∴AB是△ABE外接圆的直径.
在Rt△ABE中,tan∠BAE===tan∠CBE,
∴∠BAE=∠CBE.
在Rt△ABE中,∠BAE+∠3=90°,∴∠CBE+∠3=90°.
∴∠CBA=90°,即CB⊥AB.
∴CB是△ABE外接圆的切线.
(3)解:Rt△ABE中,∠AEB=90°,tan∠BAE=,sin∠BAE=,cos∠BAE=;
若以D、E、P为顶点的三角形与△ABE相似,则△DEP必为直角三角形;
①DE为斜边时,P1在x轴上,此时P1与O重合;
由D(﹣1,0)、E(0,3),得OD=1、OE=3,即tan∠DEO==tan∠BAE,即∠DEO=∠BAE
满足△DEO∽△BAE的条件,因此
O点是符合条件的P1点,坐标为(0,0).
②DE为短直角边时,P2在x轴上;
若以D、E、P为顶点的三角形与△ABE相似,则∠DEP2=∠AEB=90°,sin∠DP2E=sin∠BAE=;
而DE==,则DP2=DE÷sin∠DP2E=÷=10,OP2=DP2﹣OD=9
即:P2(9,0);
③DE为长直角边时,点P3在y轴上;
若以D、E、P为顶点的三角形与△ABE相似,则∠EDP3=∠AEB=90°,cos∠DEP3=cos∠BAE=;
则EP3=DE÷cos∠DEP3=÷=,OP3=EP3﹣OE=;
综上,得:P1(0,0),P2(9,0),P3(0,﹣).
(4)解:设直线AB的解析式为y=kx+b.
将A(3,0),B(1,4)代入,得:解得:
∴y=﹣2x+6.
过点E作射线EF∥x轴交AB于点F,当y=3时,得x=,∴F(,3).
情况一:如图2,当0<t≤时,设△AOE平移到△DNM的位置,MD交AB于点H,MN交AE于点G.
则ON=AD=t,过点H作LK⊥x轴于点K,交EF于点L.
由△AHD∽△FHM,得:=,即=.
解得HK=2t.
∴S阴=S△MND﹣S△GNA﹣S△HAD=×3×3﹣(3﹣t)2﹣t 2t=﹣t2+3t.
情况二:如图3,当<t≤3时,设△AOE平移到△PQR的位置,PQ交AB于点I,交AE于点V.
由△IQA∽△IPF,得:=.即=,
解得IQ=2(3﹣t).
∴S阴=S△IQA﹣S△VQA=×(3﹣t)×2(3﹣t)﹣(3﹣t)2=(3﹣t)2=t2﹣3t+.
综上所述:s=.
锐角三角函数
同步练习
一、单选题
1、如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①tan∠AEC=;②S△ABC+S△CDE≥S△ACE;③BM⊥DM;④BM=DM.正确结论的个数是( )
A、1个
B、2个
C、3个
D、4个
2、在△ABC中,∠C=90°,AB=6,BC=2,则下列三角函数表示正确的是( )
A、sinA=
B、cosB=2
C、tanA=
D、cosA=
3、已知α是锐角,cosα=,
则tanα的值是( )
A、
B、
C、3
D、
4、如果α是锐角,且cosα=,那么sinα的值是(
)
A、
B、
C、
D、
5、已知△ABC中,∠C=90°,tanA=
,
D是AC上一点,∠CBD=∠A,则sin∠ABD=(
)
A、
B、
C、
D、
6、如图,P是∠α的边OA上一点,点P的坐标为(12,5),则tanα等于
A、
B、
C、
D、
7、Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c,且a:b=3:4,斜边c=15,则b的值是( )
A、12
B、9
C、4
D、3
8、如图,已知⊙O的半径为5,AB=8,
锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )
A、
B、
C、
D、
9、如图,在□ABCD中,AB∶AD=3∶2,∠ADB=60°,那么cosA的值等于( )
A、
B、
C、
D、
10、已知α、β都是锐角,如果sinα=cosβ,那么α与β之间满足的关系是( )
A、α=β;
B、α+β=90°;
C、α-β=90°;
D、β-α=90°.
11、已知α为锐角,则m=sin2α+cos2α的值( )
A、m>1
B、m=1
C、m<1
D、m≥1
12、图1,在Rt△ABC中,∠ACB=90°,点P以每秒1cm的速度从点A出发,沿折线AC-CB运动,到点B停止,过点P作PD⊥AB,垂足为D,PD的长y(cm)与点P的运动时间x(秒)的函数图象如图2所示,当点P运动5秒时,PD的长是(
)
A、1.5cm
B、1.2cm
C、1.8cm
D、2cm
13、如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,),点C的坐标为(,0),点P为斜边OB上的一动点,则PA+PC的最小值为
A、
B、
C、
D、2
14、已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3在x轴上.若正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3
,
则点A3到x轴的距离是( )
A、
B、
C、
D、
二、填空题
15、求值:________
16、已知α是锐角且tanα=,
则sinα+cosα=________
17、在Rt△ABC中,∠C=90°,sin∠A=,
则tan∠B的值为________
18、已知α、β均为锐角,且满足|sinα﹣|+=0,则α+β= ________.
19、如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30o得到正方形AB′C′D′,则它们的公共部分的面积等于________
。
三、计算题
20、计算:
21、
(1)计算:
4cos245°-|-2|
+
tan45°;
(2)分解因式:
四、解答题
22、已知tanα=,
α是锐角,求tan(9O°﹣α),sinα,cosα的值.
23、已知[4(xy﹣1)2﹣(xy+2)(2﹣xy)]÷xy,其中x=(﹣cos60°)﹣1
,
y=﹣sin30°.
24、如图,点C在⊙O的直径BA的延长线上,AB=2AC,CD切⊙O于点D,连接CD,OD.
(1)求角C的正切值:
(2)若⊙O的半径r=2,求BD的长度.
25、如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE=,A(3,0),D(﹣1,0),E(0,3).
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由;
(4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE与△ABE重叠部分的面积为s,求s与t之间的函数关系式,并指出t的取值范围.
答案部分
一、单选题
1、
【答案】D
2、
【答案】C
3、
【答案】B
4、
【答案】C
5、
【答案】A
6、
【答案】C
7、
【答案】A
8、
【答案】A
9、
【答案】A
10、
【答案】B
11、
【答案】B
12、
【答案】B
13、
【答案】B
14、
【答案】D
二、填空题
15、
【答案】
16、
【答案】
17、
【答案】
18、
【答案】75°
19、
【答案】
三、计算题
20、
【答案】解:原式==9+8+1-3=15.
21、
【答案】解:(1)
4cos245°-|-2|
+
tan45°
=4x-2+1
=4x-1
=2-1
=1
(2)分解因式:
=a(-9)
=a(a-3)(a+3)
四、解答题
22、
【答案】解:∵如图所示:tanB=tanα=,
∴设AC=2x,BC=5x,则AB=x,
∴tan(9O°﹣α)==,
sinα===,
cosα===.
23、
【答案】解:∵x=(﹣cos60°)﹣1=(﹣)﹣1=﹣2,y=﹣sin30°=﹣,
∴[4(xy﹣1)2﹣(xy+2)(2﹣xy)]÷xy
=[4(x2y2﹣2xy+1)﹣(22﹣x2y2)]
=(4x2y2﹣8xy+4﹣4+x2y2)
=(5x2y2﹣8xy)
=20xy﹣32
=20×(﹣2)×(﹣)﹣32
=﹣12.
24、
【答案】解:(1)∵CD切⊙O于点D,
∴CD⊥OD,
又∵AB=2AC,
∴OD=AO=AC=CO
∴∠C=30°
∴tan∠C=;
(2)连接AD,
∵AB是直径,
∴∠ADB=90°,
∵∠DOA=90°﹣30°=60°,
又∵OD=OA,
∴△DAO是等边三角形.
∴DA=r=2,
∴DB==.
25、
【答案】(1)解:由题意,设抛物线解析式为y=a(x﹣3)(x+1).
将E(0,3)代入上式,解得:a=﹣1.
∴y=﹣x2+2x+3.
则点B(1,4).
(2)证明:如图1,过点B作BM⊥y于点M,则M(0,4).
在Rt△AOE中,OA=OE=3,
∴∠1=∠2=45°,AE==3.
在Rt△EMB中,EM=OM﹣OE=1=BM,
∴∠MEB=∠MBE=45°,BE==.
∴∠BEA=180°﹣∠1﹣∠MEB=90°.
∴AB是△ABE外接圆的直径.
在Rt△ABE中,tan∠BAE===tan∠CBE,
∴∠BAE=∠CBE.
在Rt△ABE中,∠BAE+∠3=90°,∴∠CBE+∠3=90°.
∴∠CBA=90°,即CB⊥AB.
∴CB是△ABE外接圆的切线.
(3)解:Rt△ABE中,∠AEB=90°,tan∠BAE=,sin∠BAE=,cos∠BAE=;
若以D、E、P为顶点的三角形与△ABE相似,则△DEP必为直角三角形;
①DE为斜边时,P1在x轴上,此时P1与O重合;
由D(﹣1,0)、E(0,3),得OD=1、OE=3,即tan∠DEO==tan∠BAE,即∠DEO=∠BAE
满足△DEO∽△BAE的条件,因此
O点是符合条件的P1点,坐标为(0,0).
②DE为短直角边时,P2在x轴上;
若以D、E、P为顶点的三角形与△ABE相似,则∠DEP2=∠AEB=90°,sin∠DP2E=sin∠BAE=;
而DE==,则DP2=DE÷sin∠DP2E=÷=10,OP2=DP2﹣OD=9
即:P2(9,0);
③DE为长直角边时,点P3在y轴上;
若以D、E、P为顶点的三角形与△ABE相似,则∠EDP3=∠AEB=90°,cos∠DEP3=cos∠BAE=;
则EP3=DE÷cos∠DEP3=÷=,OP3=EP3﹣OE=;
综上,得:P1(0,0),P2(9,0),P3(0,﹣).
(4)解:设直线AB的解析式为y=kx+b.
将A(3,0),B(1,4)代入,得:解得:
∴y=﹣2x+6.
过点E作射线EF∥x轴交AB于点F,当y=3时,得x=,∴F(,3).
情况一:如图2,当0<t≤时,设△AOE平移到△DNM的位置,MD交AB于点H,MN交AE于点G.
则ON=AD=t,过点H作LK⊥x轴于点K,交EF于点L.
由△AHD∽△FHM,得:=,即=.
解得HK=2t.
∴S阴=S△MND﹣S△GNA﹣S△HAD=×3×3﹣(3﹣t)2﹣t 2t=﹣t2+3t.
情况二:如图3,当<t≤3时,设△AOE平移到△PQR的位置,PQ交AB于点I,交AE于点V.
由△IQA∽△IPF,得:=.即=,
解得IQ=2(3﹣t).
∴S阴=S△IQA﹣S△VQA=×(3﹣t)×2(3﹣t)﹣(3﹣t)2=(3﹣t)2=t2﹣3t+.
综上所述:s=.
