2.1.1 直线和圆的位置关系 课件
图片预览








文档简介
课件20张PPT。第二章 直线与圆的位置关系2.1.1 直线和圆的位置关系情境导入生活离不开圆生活离不开圆,车轮是圆的才可以行驶,转动的摩天轮是圆的等等。那么行驶的车轮和地面又是什么关系?观察日出的三幅照片你发现这个自然现象反映出直线和圆的位置关系有哪几种?a(地平线)情境导入感悟新知(2) 当直线与圆有唯一公共点时,叫做直线与圆 .(3) 当直线与圆没有公共点时,叫做直线与圆 . (1) 当直线与圆有两个公共点时,叫做直线与圆 . 相离相切相交(1)(3)(2)这条直线叫做圆的切线,公共点叫做切点。OOO直线与圆的位置关系这条直线叫圆的割线; 公共点叫直线与圆的交点。相离相切相交切线切点割线思考:直线与圆有第四种关系吗?(即一条直线和一个圆如果有公共点,公共点的个数能不能多于两个呢?)想一想练习 1、直线与圆最多有两个公共
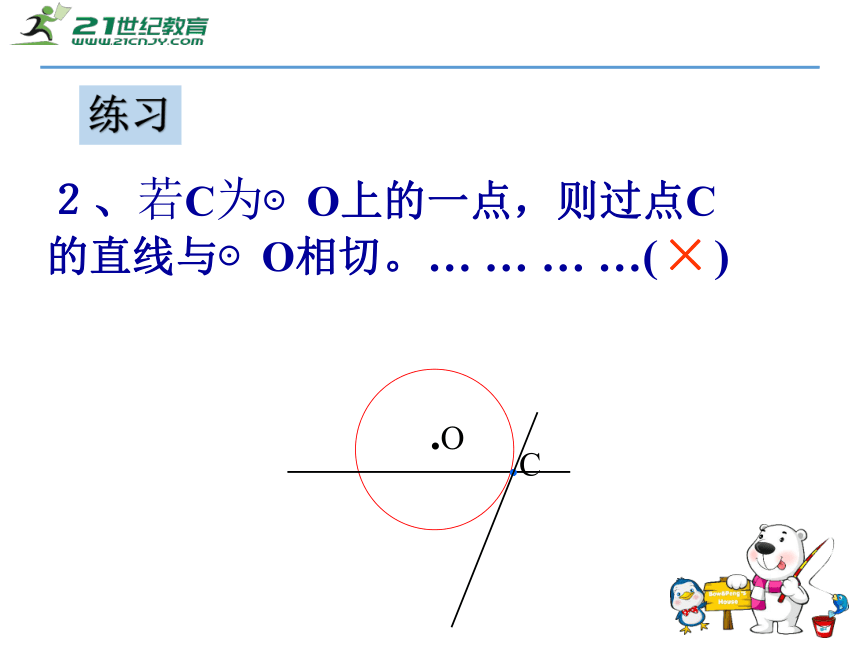
点 。…………………( ) √×.C2、若C为⊙O上的一点,则过点C的直线与⊙O相切。… … … …( )练习√3、若C为⊙O内一点,则过点C的直线与⊙O相交。( )练习4、若A、B是⊙O外两点, 则直线AB
与⊙O相离。… … … … …( )×练习小问题: 直线与圆的公共点的个数新的问题:如果直线与圆的公共点的个数不好判断,该怎么办?是否还有其他的方法来判断直线与圆的位置关系?能否根据基本概念来判断直线与圆的位置关系? 如图,O为直线l外一点,OT⊥l,且OT=d,请以O为圆心,分别以 r > d, r=d, r < d 为半径画圆。
思考:
(1)观察所画的圆与直线l分别有什么位置关系?(2)你觉得直线与圆的位置关系与哪些量有关? 深入探究 “直线和圆的位置关系”能否像“点和圆的位置关系”一样进行数量分析?通过观察所画的圆与直线l,我们能够发现直线与圆的位置与圆的半径r和圆心到直线的距离d有关。 思考怎样判定点和圆的位置关系?.A . B.C(1)点到圆心的距离____半径时,点在圆外。
(2)点到圆心的距离____半径时,点在圆上。
(3)点到圆心的距离____半径时,点在圆内。大于等于小于点在圆上 点在圆外点在圆内d=rd相离相切相交例1 已知:如图,P为∠ABC的角平分线上一点, ⊙P与BC相切. 求证:⊙P与AB相切.
设⊙P的半径为r,点P到BC,
AB的距离分别为d1,d2.
∵点P在∠ABC的平分线上,
∴ d1=d2.
又⊙P与BC相切,
∴ d1=r,则d2=r.
∴ ⊙P与AB相切.证明: 总结判定直线与圆的位置关系的方法有____种:(1)由________________ 的个数来判断;(2)由__________________________的数量大小关系来判断.注意:
在实际应用中,常采用第二种方法判定.两直线 与圆的公共点圆心到直线的距离d与半径r
例2 如图,在码头A的北偏东60°方向有一个海岛,离该岛中心P的12海里范围内是一个暗礁区。货船从码头A由西向东方向航行,行驶了10海里到达B,这时岛中心P在北偏东45°方向。若货船不改变航向,问货船会不会进入暗礁区?北H暗礁区解:如图,作PH⊥AB,垂足为H.则∠PAH=30°∠PBH=45°,∴货船不会进入暗礁区∵AH-BH=AB=10∵13.66>12 如图,在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,设⊙C的半径为r,请根据下列r的值,判断直线AB与⊙C的位置关系,并说明理由。
(1)r=2cm;(2)r=2.4cm; (3)r=3cm。d分析:
过点C作CD⊥AB,交AB于点D
CD?AB=AC?BC,
求得CD=2.4,即d=2.4 练习直线与圆的三种位置关系2 个交点割线1 个切点切线d < rd = rd > r没有相交相切相离课堂小结课后作业完成教材P36作业题T1-T6谢谢
点 。…………………( ) √×.C2、若C为⊙O上的一点,则过点C的直线与⊙O相切。… … … …( )练习√3、若C为⊙O内一点,则过点C的直线与⊙O相交。( )练习4、若A、B是⊙O外两点, 则直线AB
与⊙O相离。… … … … …( )×练习小问题: 直线与圆的公共点的个数新的问题:如果直线与圆的公共点的个数不好判断,该怎么办?是否还有其他的方法来判断直线与圆的位置关系?能否根据基本概念来判断直线与圆的位置关系? 如图,O为直线l外一点,OT⊥l,且OT=d,请以O为圆心,分别以 r > d, r=d, r < d 为半径画圆。
思考:
(1)观察所画的圆与直线l分别有什么位置关系?(2)你觉得直线与圆的位置关系与哪些量有关? 深入探究 “直线和圆的位置关系”能否像“点和圆的位置关系”一样进行数量分析?通过观察所画的圆与直线l,我们能够发现直线与圆的位置与圆的半径r和圆心到直线的距离d有关。 思考怎样判定点和圆的位置关系?.A . B.C(1)点到圆心的距离____半径时,点在圆外。
(2)点到圆心的距离____半径时,点在圆上。
(3)点到圆心的距离____半径时,点在圆内。大于等于小于点在圆上 点在圆外点在圆内d=rd
设⊙P的半径为r,点P到BC,
AB的距离分别为d1,d2.
∵点P在∠ABC的平分线上,
∴ d1=d2.
又⊙P与BC相切,
∴ d1=r,则d2=r.
∴ ⊙P与AB相切.证明: 总结判定直线与圆的位置关系的方法有____种:(1)由________________ 的个数来判断;(2)由__________________________的数量大小关系来判断.注意:
在实际应用中,常采用第二种方法判定.两直线 与圆的公共点圆心到直线的距离d与半径r
例2 如图,在码头A的北偏东60°方向有一个海岛,离该岛中心P的12海里范围内是一个暗礁区。货船从码头A由西向东方向航行,行驶了10海里到达B,这时岛中心P在北偏东45°方向。若货船不改变航向,问货船会不会进入暗礁区?北H暗礁区解:如图,作PH⊥AB,垂足为H.则∠PAH=30°∠PBH=45°,∴货船不会进入暗礁区∵AH-BH=AB=10∵13.66>12 如图,在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,设⊙C的半径为r,请根据下列r的值,判断直线AB与⊙C的位置关系,并说明理由。
(1)r=2cm;(2)r=2.4cm; (3)r=3cm。d分析:
过点C作CD⊥AB,交AB于点D
CD?AB=AC?BC,
求得CD=2.4,即d=2.4 练习直线与圆的三种位置关系2 个交点割线1 个切点切线d < rd = rd > r没有相交相切相离课堂小结课后作业完成教材P36作业题T1-T6谢谢
