2.3 三角形的内切圆 课件
图片预览


文档简介
课件19张PPT。第二章 直线与圆的位置关系2.3 三角形的内切圆课时导入 这条美丽的花边图案主要是由哪些几何图形组成的?它们之间有着怎样的位置关系? 这条美丽的花边图案,同学们是否也可以轻易的画出来?今天我们一起去探讨一下!回顾旧知1、切线长定理
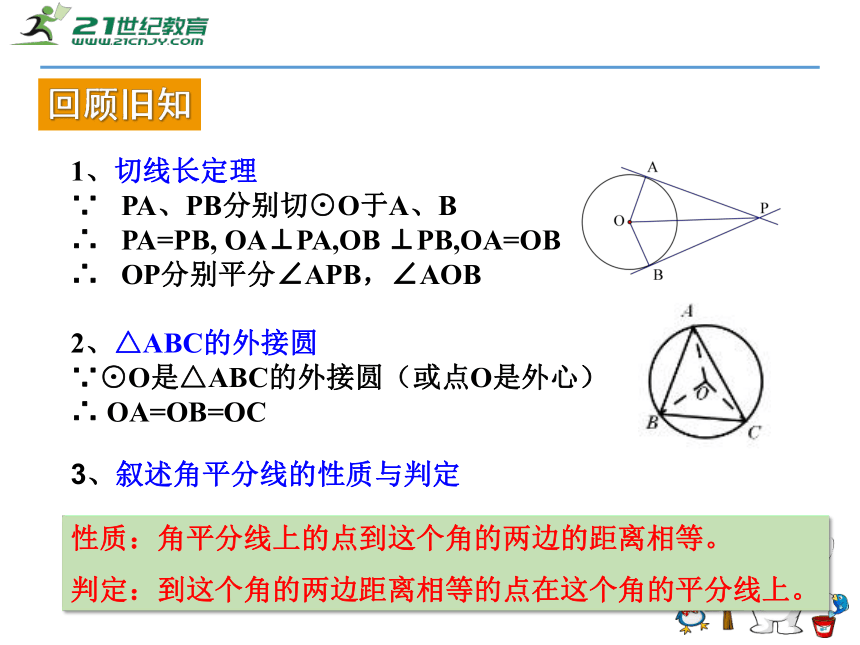
∵ PA、PB分别切⊙O于A、B
∴ PA=PB, OA⊥PA,OB ⊥PB,OA=OB
∴ OP分别平分∠APB,∠AOB
2、△ABC的外接圆
∵⊙O是△ABC的外接圆(或点O是外心)
∴ OA=OB=OC
3、叙述角平分线的性质与判定性质:角平分线上的点到这个角的两边的距离相等。
判定:到这个角的两边距离相等的点在这个角的平分线上。如图,要从一块三角形钢化玻璃上裁下一个半径尽可能大的
圆来做一圆桌的桌面,应该怎样画出裁剪的图样呢?
建议按下列步骤探索:
(1) 当裁得的圆最大时,圆与三角形的各边有什么位置关系?
(2)与三角形的一个角的两边都相切
的圆的圆心在哪里?
(3)如何确定这个圆的圆心和半径?
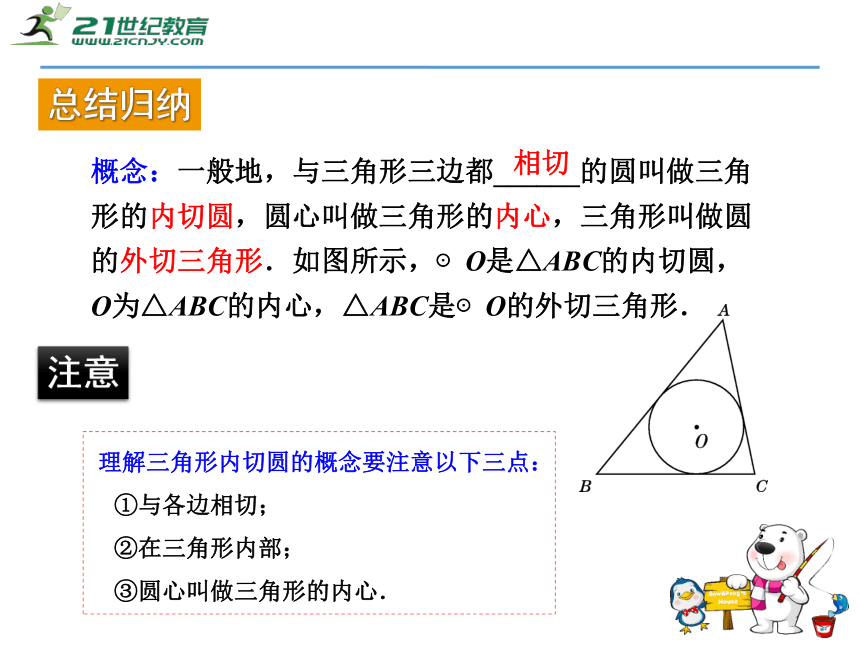
合作探究概念:一般地,与三角形三边都______的圆叫做三角
形的内切圆,圆心叫做三角形的内心,三角形叫做圆
的外切三角形.如图所示,⊙O是△ABC的内切圆,
O为△ABC的内心,△ABC是⊙O的外切三角形.相切总结归纳 理解三角形内切圆的概念要注意以下三点:
①与各边相切;
②在三角形内部;
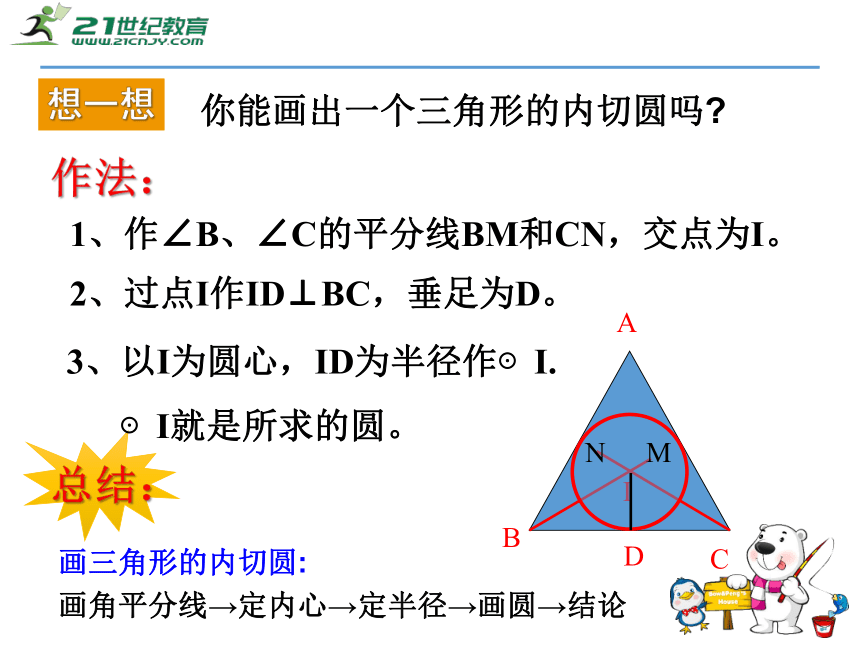
③圆心叫做三角形的内心.注意想一想你能画出一个三角形的内切圆吗?作法: ABC1、作∠B、∠C的平分线BM和CN,交点为I。 I2、过点I作ID⊥BC,垂足为D。 3、以I为圆心,ID为半径作⊙I.
⊙I就是所求的圆。 MN画三角形的内切圆:
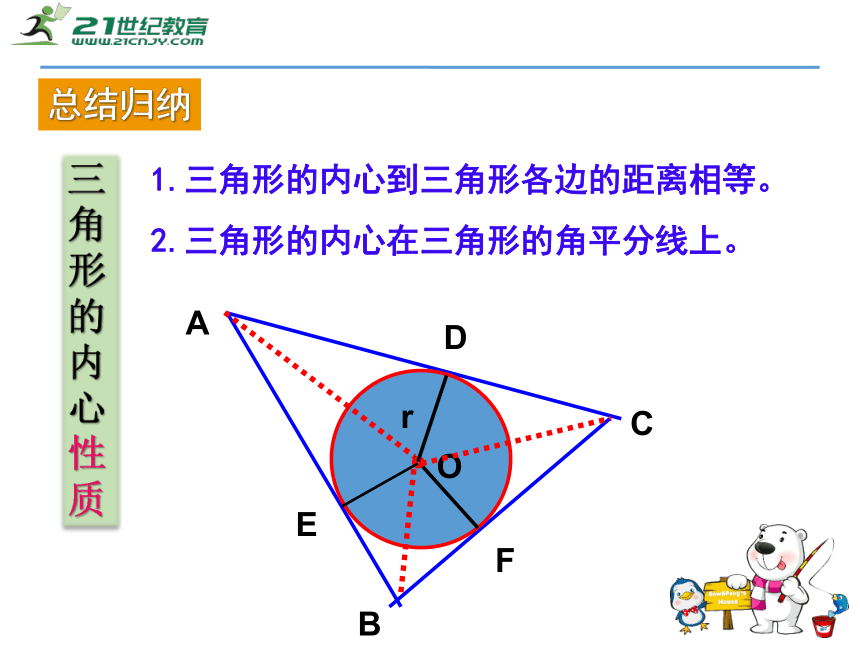
画角平分线→定内心→定半径→画圆→结论总结: 1.三角形的内心到三角形各边的距离相等。三角形的内心性质Or2.三角形的内心在三角形的角平分线上。总结归纳内心、外心的区别与联系 (如下表):比一比(1)在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别
为a、b、c,则其内切圆的半径
(2)若△ABC的周长为l,内切圆的半径为r,则△ABC的面积
S= lr.
(3)四边形的内心与任一顶点的连线平分四边形的内角.
易错提示:
(1)三角形的内切圆只有一个.
(2)三角形的内心一定在三角形内部.
拓展结论例1 如图,等边三角形ABC的边长为3 cm,求△ABC的内切圆⊙O的半径.如图,设⊙O切AB于点D,连结OA,OB,OD.
∵ ⊙O是△ABC的内切圆,
∴AO,BO 是∠BAC, ∠ABC,
的角平分线.
∵△ABC是等边三角形,
∴∠OAB=∠OBA = 30°. 解:例题讲解∵OD⊥AB,AB=3cm,
∴AD=BD= AB=1.5(cm),
∴OD=AD×tan30°
答:△ABC的内切圆的半径为 总结:见切点,连半径,结合等腰三角形、等边三角形的性质求出半径长.例2 已知:如图, ⊙O是△ABC的内切圆,切点分别为D,E,F.设△ABC的周长为l,求证: AE+BC= l.∵⊙O是△ABC的内切圆,E,F为切点,
∴AE=AF(根据什么?).
同理,BD=BF,CD=CE.
∴AE+BC=AE+BD+CD
= (AE+AF+BD+BF+CD+CE)
=
证明:总结:解答有关问题时,常与切线长定理联系.1、如图,⊙O内切于Rt△ABC,∠ACB=90°,若∠CBO=30°,则∠A等于( )
A.15°
B.30°
C.45°
D.60°课堂练习2 、 如图,正三角形的内切圆的半径为1,那么正三角形的边长为( )
A.2
B.2
C.
D.33 、如图,点O是△ABC的内心,若∠ACB=70°,则∠AOB=( )
A.140°
B.135°
C.125°
D.110°4、如图,I是?ABC的内心,连结AI并延长交BC边于点D,交?ABC的外接圆于点E. 求证:(1) EI = EB ;(2)IE 2 = AE · DE .EDF 5、如图,朱家镇在进入镇区的道路交叉口的三角地处建造了一座镇标雕塑,以树立起文明古镇的形象。已知雕塑中心M到道路三边AC、BC、AB的距离相等,AC⊥BC,BC=30米,AC=40米。请你帮助计算一下,镇标雕塑中心M离道路三边的距离有多远?M1. 三角形的内切圆中“切”是指三角形的三边与圆的
位置关系.
2. 一个三角形只有一个内切圆,而圆的外切三角形有
无数个;三角形的内切圆一定在这个三角形的内部.
3. 三角形内切圆的圆心是三角形内角平分线的交点,
称为内心,它到这个三角形三边的距离相等.课堂小结圆的问题三角形、四边形问题连结内心与切点或顶点转化完成教材P49、50作业题T1-T5课后作业谢谢
∵ PA、PB分别切⊙O于A、B
∴ PA=PB, OA⊥PA,OB ⊥PB,OA=OB
∴ OP分别平分∠APB,∠AOB
2、△ABC的外接圆
∵⊙O是△ABC的外接圆(或点O是外心)
∴ OA=OB=OC
3、叙述角平分线的性质与判定性质:角平分线上的点到这个角的两边的距离相等。
判定:到这个角的两边距离相等的点在这个角的平分线上。如图,要从一块三角形钢化玻璃上裁下一个半径尽可能大的
圆来做一圆桌的桌面,应该怎样画出裁剪的图样呢?
建议按下列步骤探索:
(1) 当裁得的圆最大时,圆与三角形的各边有什么位置关系?
(2)与三角形的一个角的两边都相切
的圆的圆心在哪里?
(3)如何确定这个圆的圆心和半径?
合作探究概念:一般地,与三角形三边都______的圆叫做三角
形的内切圆,圆心叫做三角形的内心,三角形叫做圆
的外切三角形.如图所示,⊙O是△ABC的内切圆,
O为△ABC的内心,△ABC是⊙O的外切三角形.相切总结归纳 理解三角形内切圆的概念要注意以下三点:
①与各边相切;
②在三角形内部;
③圆心叫做三角形的内心.注意想一想你能画出一个三角形的内切圆吗?作法: ABC1、作∠B、∠C的平分线BM和CN,交点为I。 I2、过点I作ID⊥BC,垂足为D。 3、以I为圆心,ID为半径作⊙I.
⊙I就是所求的圆。 MN画三角形的内切圆:
画角平分线→定内心→定半径→画圆→结论总结: 1.三角形的内心到三角形各边的距离相等。三角形的内心性质Or2.三角形的内心在三角形的角平分线上。总结归纳内心、外心的区别与联系 (如下表):比一比(1)在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别
为a、b、c,则其内切圆的半径
(2)若△ABC的周长为l,内切圆的半径为r,则△ABC的面积
S= lr.
(3)四边形的内心与任一顶点的连线平分四边形的内角.
易错提示:
(1)三角形的内切圆只有一个.
(2)三角形的内心一定在三角形内部.
拓展结论例1 如图,等边三角形ABC的边长为3 cm,求△ABC的内切圆⊙O的半径.如图,设⊙O切AB于点D,连结OA,OB,OD.
∵ ⊙O是△ABC的内切圆,
∴AO,BO 是∠BAC, ∠ABC,
的角平分线.
∵△ABC是等边三角形,
∴∠OAB=∠OBA = 30°. 解:例题讲解∵OD⊥AB,AB=3cm,
∴AD=BD= AB=1.5(cm),
∴OD=AD×tan30°
答:△ABC的内切圆的半径为 总结:见切点,连半径,结合等腰三角形、等边三角形的性质求出半径长.例2 已知:如图, ⊙O是△ABC的内切圆,切点分别为D,E,F.设△ABC的周长为l,求证: AE+BC= l.∵⊙O是△ABC的内切圆,E,F为切点,
∴AE=AF(根据什么?).
同理,BD=BF,CD=CE.
∴AE+BC=AE+BD+CD
= (AE+AF+BD+BF+CD+CE)
=
证明:总结:解答有关问题时,常与切线长定理联系.1、如图,⊙O内切于Rt△ABC,∠ACB=90°,若∠CBO=30°,则∠A等于( )
A.15°
B.30°
C.45°
D.60°课堂练习2 、 如图,正三角形的内切圆的半径为1,那么正三角形的边长为( )
A.2
B.2
C.
D.33 、如图,点O是△ABC的内心,若∠ACB=70°,则∠AOB=( )
A.140°
B.135°
C.125°
D.110°4、如图,I是?ABC的内心,连结AI并延长交BC边于点D,交?ABC的外接圆于点E. 求证:(1) EI = EB ;(2)IE 2 = AE · DE .EDF 5、如图,朱家镇在进入镇区的道路交叉口的三角地处建造了一座镇标雕塑,以树立起文明古镇的形象。已知雕塑中心M到道路三边AC、BC、AB的距离相等,AC⊥BC,BC=30米,AC=40米。请你帮助计算一下,镇标雕塑中心M离道路三边的距离有多远?M1. 三角形的内切圆中“切”是指三角形的三边与圆的
位置关系.
2. 一个三角形只有一个内切圆,而圆的外切三角形有
无数个;三角形的内切圆一定在这个三角形的内部.
3. 三角形内切圆的圆心是三角形内角平分线的交点,
称为内心,它到这个三角形三边的距离相等.课堂小结圆的问题三角形、四边形问题连结内心与切点或顶点转化完成教材P49、50作业题T1-T5课后作业谢谢
