2.2.1 因式分解法 课件

课件14张PPT。第二章 一元二次方程2.2.1 因式分解法2.2 一元二次方程的解法回顾旧知（a≠0） 1、一元二次方程的定义2、一元二次方程的一般式： ①方程两边都是整式②只含有一个未知数③未知数的最高次数是2次3、因式分解: 把一个多项式化成几个整式的积的形式主要方法:(1)提取公因式法:a2－ab=a(a－b)(2)公式法: a2－b2=(a+b)(a－b)a2±2ab+b2=(a±b)21. 若A×B = 0,下面两个结论正确吗？
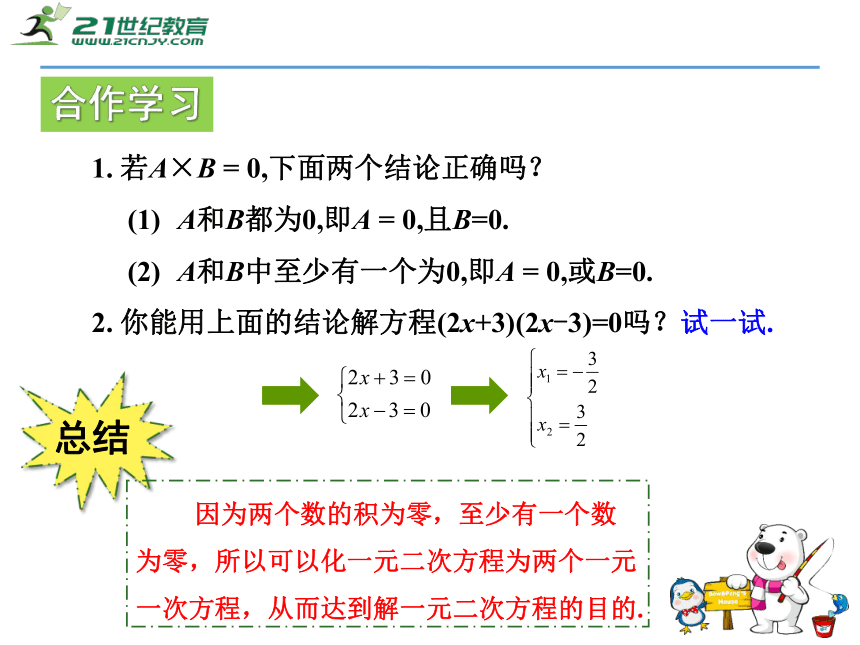
(1) A和B都为0,即A = 0,且B=0.
(2) A和B中至少有一个为0,即A = 0,或B=0.
2. 你能用上面的结论解方程(2x+3)(2x-3)=0吗？试一试.合作学习总结 因为两个数的积为零，至少有一个数为零，所以可以化一元二次方程为两个一元一次方程，从而达到解一元二次方程的目的. 先把方程转化为两个一元一次方程，然后分别解
答即可.1 解下列方程：(1) x(5x－4)=0， (2) (x－2)(1－x)=0 解析：解：(1) x(5x－4)=0，x=0或5x -4=0,
∴x1=0或x2=
(2) (x－2)(1－x)=0, x－2=0或1－x=0，
∴x1=2，x2=1.做一做解方程：(x＋4)(x－1)＝6.解：将原方程化为标准形式，得
x2＋3x－10＝0.
把方程左边分解因式，得
(x＋5)(x－2)＝0.
∴x＋5＝0或x－2＝0.
解方程，得
x1＝－5，x2＝2.2 解答1和2此类一元二次方程的方法总结为：
一化（把方程转化为一次方程）
二写（写出原方程的解）像上面这种利用因式分解解一元二次方程的方法叫做因式分解法。(1)将原方程的左边分解因式，得x(x－3)＝0.
则 x＝0或x－3＝0.
解得 x1＝0, x2＝3.例1解下列方程: (1)x2－3x＝0 (2)25x2=16解：例题讲解?总结(1)化简方程，得3x2－17x＝0
将方程的左边因式分解，得
x(3x－17)＝0.
则 x＝0或3x－17＝0.
解得 x1＝0, x2＝解下列一元二次方程:
(1)(x－5) (3x－2)＝10
(2)例2解：例题讲解(2) (3x－4)2=(4x－3)2.(2)移项，得（3x－4)2－(4x－3)2=0.
将方程的左边分解因式，得
〔(3x－4)+(4x－3)〕〔(3x－4)－(4x－3)〕=0,
即 (7x－7) (-x－1)=0.
∴7x－7=0,或 -x－1=0.
∴x1=1, x2=-1例题讲解解：（1）将方程变形，使方程的右边为零；（2）将方程的左边因式分解；（3）根据若A·B=0，则A=0或B=0，将解一元二次方程转 化为解两个一元一次方程；因式分解法的基本步骤：总结归纳注意： 分解因式法的条件是方程左边易于分解，而右边等于零，关键是熟练掌握分解因式的知识，理论依旧是“如果两个因式的积等于零，那么至少有一个因式等于零．”
“至少”有下列三层含义
① A＝0且B≠0 ②A≠0且B＝0 ③A＝0且B＝0移项，得x2 － x +2＝0，
即
则
解得 x1＝x2＝例3解下列方程: x2＝2 x－2.解：例题讲解用因式分解法解下列方程:
(1) 7x2＝21x；
(2) (x＋2)2＝2x＋4. 课堂练习 (3)
(4) 27x2-18x= -3.
(5) (7x-1)2= 4x2. 3 若(x－2)2＋6(x－2)＋9＝0，则x的值为(　　)
A．0 B．－1 C．1 D．－2课堂练习2 方程2x(x－5)＝6(x－5)的根是(　　)
A．x＝5 B．x＝－5
C．x1＝－5，x2＝3 D．x1＝5，x2＝3小华在解一元二次方程x2－4x＝0时，只得出一个
根是x＝4，则被他漏掉的一个根是x＝________.用因式分解法解一元二次方程的步骤：
(1) 移项，将方程的右边化为0；
(2) 将方程的左边分解为两个一次因式的积；
(3) 令每个因式等于0，得两个一元一次方程；
(4) 解这两个一元一次方程，得方程的两个根．
用因式分解法解方程的关键是将方程左边因式分解.
常用到的因式分解的方法是：提公因式法、公式法、
x2－(a＋b)x＋ab型的因式分解(即十字相乘法)．课堂小结完成教材P31作业题T1-T6课后作业谢谢