2.2.2 开平方法 课件

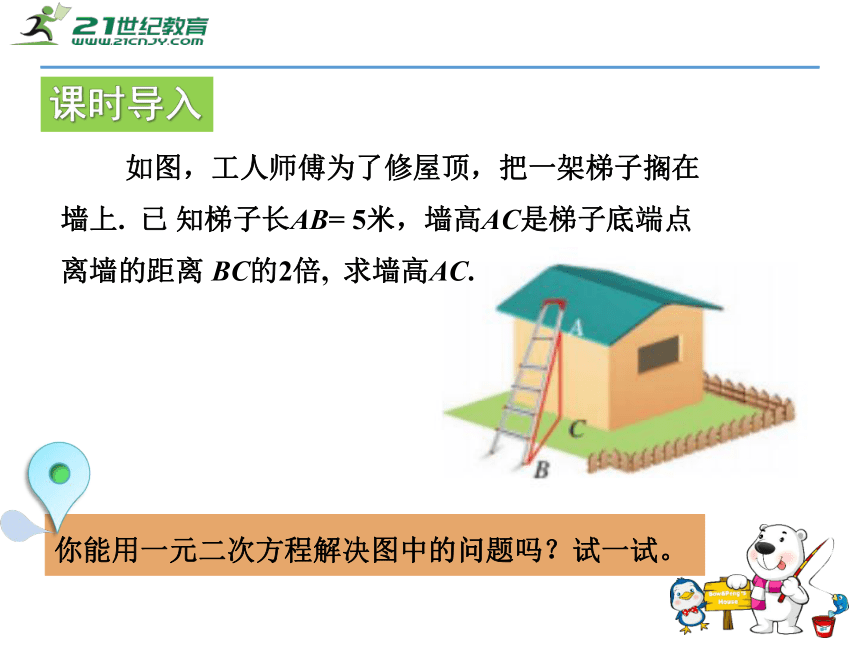
课件16张PPT。第二章 一元二次方程2.2.2 开平方法2.2 一元二次方程的解法 如图，工人师傅为了修屋顶，把一架梯子搁在
墙上. 已 知梯子长AB= 5米，墙高AC是梯子底端点
离墙的距离 BC的2倍, 求墙高AC.课时导入你能用一元二次方程解决图中的问题吗？试一试。回顾旧知（1）将方程变形，使方程的右边为零；（2）将方程的左边因式分解；（3）根据若A·B=0，则A=0或B=0，将解一元二次方程转 化为解两个一元一次方程；因式分解法的基本步骤： 上节课，我们学习了用因式分解法解一元二次方程。接下来我们将学习第二种一元二次方程的解法。形如x2＝p(p≥0)的一元二次方程的解法1．定义：根据平方根的定义，直接开平方求一元二
次方程的解的方法叫做开平方法．
2．开平方法求方程的解的方法：
x2＝p(p≥0)→x＝合作学习1(1)移项，得x2＝81，于是x＝±9，
即x1＝9，x2＝－9.
(2)移项，得4x2＝64，于是x2＝16，
所以x＝±4，即x1＝4，x2＝－4.解：用开平方法解下列方程：
(1)x2－81＝0；(2)4x2－64＝0；1 做一做总结：用开平方法解一元二次方程时，首先将方程化成左边是含有未知数的完全平方式，右边是非负数的形式，然后根据平方根的意义求解．当整理后右边为0时，方程有两个相等的实数根．形如(mx＋n)2＝p(p≥0)的一元二次方程的解法开平方法求方程的解的方法：
(1)(x＋a)2＝p(p≥0)→x＝
(2)(mx＋n)2＝p(p≥0，m≠0)→x＝合作学习2(1)x－3＝±5，于是x1＝8，x2＝－2.
(2)2y－3＝±4，于是y1＝ ，y2＝－ .2用开平方法解下列方程：
(1)(x－3)2＝25； (2)(2y－3)2＝16.解：做一做(1)移项，得3x2＝48.
方程的两边同除以3，得x2＝16.
解得x1＝4，x2＝－4.
(2)由原方程，得2x－3＝ ，或2x －3＝－
解得x1＝ ，x2＝ .例4 用开平方法解下列方程：
(1)3x2－48＝0； (2)(2x－3)2＝7.解：例题讲解 （ax+b）2=c（ c≥0）的方程可以直接运用“开平方法”求解．开平方法实质上是把一个一元二次方程通过求一个代数式的平方根，从而把方程“降次”转化为两个一元一次方程.再按一元一次方程的解法去求解.总结归纳2 若方程x2＝m的解是有理数，则实数m不能取下列四个数中的(　　)
A．1 B．4 C. D.3　 对于方程x2＝m－1，
(1)若方程有两个不相等的实数根，则m________；
(2)若方程有两个相等的实数根，则m________；
(3)若方程无实数根，则m________．1 一元二次方程x2＝4的根是(　　)
A．x＝2 B．x＝－2
C．x＝±2 D．x＝±4练习4　(中考·鞍山)已知b＜0，关于x的一元二次方程
(x－1)2＝b的根的情况是(　　)
A．有两个不相等的实数根
B．有两个相等的实数根
C．没有实数根
D．有两个实数根5 用开平方法解下列方程:
(1) (x－3)2＝16;
(2) 3(x＋1)2 = .练习利用开平方法得到 ，得到方程的两个根
互为相反数，故可求出m的值．根据m的值再求 的值．
∵x2＝ (ab＞0)，∴
∴方程的两个根互为相反数，
∴m＋1＋2m－4＝0，解得m＝1，
∴一元二次方程ax2＝b(ab＞0)的两个根分别是2与－2，
∴导引：(济宁)若一元二次方程ax2＝b(ab＞0)的两个根分别是m＋1与2m－4，则 ＝________．14拓展训练 已知某方程为一元二次方程，则此方程必须符
合一元二次方程的两个基本特征：只含一个未知数；
未知数的最高次数是2.当二次项系数是待定系数时，
还要考虑二次项系数不等于0.总结归纳开平方法求方程的解的方法：
(1) (x＋a)2＝p(p≥0)→x＝
(2) (mx＋n)2＝p(p≥0，m≠0)→x＝课堂小结(3) x2＝p(p≥0)→x＝开平方法解一元二次方程的“三步法”：
1.变形：将方程化为含未知数的完全平方式＝非负常
数的形式；
2.开方：利用平方根的定义，将方程转化为两个一元
一次方程；
3.求解：解一元一次方程，得出方程的根．课堂小结 完成教材P33课内练习T3，
教材P33-P34作业题T2课后作业谢谢