2.2.3 配方法 课件

课件21张PPT。第二章 一元二次方程2.2.3 配方法2.2 一元二次方程的解法 印度古算书中有这样一首诗：“一群猴子分两队，
高高兴兴在游戏，八分之一再平方，蹦蹦跳跳树林里；
其余十二叽喳喳，伶俐活泼又调皮，告我总数共多少，
两队猴子在一起．”
大意是说：一群猴子分成两队，一队猴子数是猴
子总数的的平方，另一队猴
子数是12，那么猴子总数是
多少？你能解决这个问题吗？课时导入1、一元二次方程的一般形式：常数项二次项， 二次项系数一次项， 一次项系数 （2）开平方法本节课将学习第三种方法：（3）配方法（1）因式分解法2、一元二次方程的解法：复习回顾探讨怎样解方程x2 - 10x= -16.
你能将方程x2 - 10x= -16转化成(x+a)2 =b的形式吗？
请尝试解这个方程.合作探究 像上面这样，把一元二次方程的左边配成一个完
全平方式，右边为一 个非负常数，然后用开平方法求
解，这种解一元二次方程的方法叫做配方法.x2 - 10x= -16 转化成 (x-5)2 =9配方就是要配成完全平方，根据完全平方式的结构
特征，当二次项系数为1时，常数项是一次项系数
一半的平方．导引：填空：
(1)x2＋10x＋________＝(x＋________)2；
(2)x2＋(________)x＋ 36＝[x＋(________)]2；
(3)x2－4x－5＝(x－________)2－______．1 25 5±12 ±6 2 9做一做(1)当二次项系数为1时，已知一次项的系数，则常数项为一次项系数一半的平方；已知常数项，则一次项系数为常数项的平方根的两倍．注意有两个．
(2)当二次项系数不为1时，则先化二次项系数为1，然后再配方．总结归纳注意：配方就是将一个多项式配成完全平方的形式．要点精析：
　对一元二次方程配方的步骤是：
①化：将方程化成一般形式，并且将二次项系数化为1；
②移：将常数项移到方程的另一边；
③配：方程两边同时加上一次项系数一半的平方．(1)方程的两边同加上9, 得 x2+6x+9=1+9,
即 (x+3)2=10.
则 x+3 = ，或x+3=
解得x1＝ x2＝例5用配方法解下列一元二次方程：
(1)x2+6x＝1； (2)x2+5x－6＝0.解：例题讲解(2)移项得 x2+5x=6.
方程的两边同加上
得x2+5x+
即
则 或
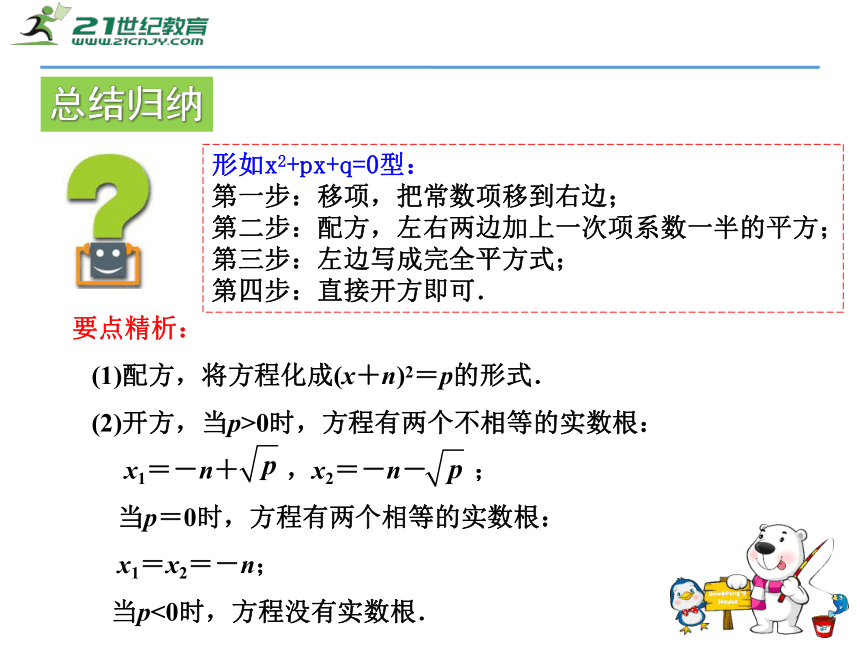
解得x1＝ 1， x2＝ －6.(2)x2+5x－6＝0.解：例题讲解形如x2+px+q=0型：
第一步：移项，把常数项移到右边；
第二步：配方，左右两边加上一次项系数一半的平方；
第三步：左边写成完全平方式；
第四步：直接开方即可．总结归纳要点精析：
(1)配方，将方程化成(x＋n)2＝p的形式．
(2)开方，当p>0时，方程有两个不相等的实数根：
x1＝－n＋ ，x2＝－n－ ；
当p＝0时，方程有两个相等的实数根：
x1＝x2＝－n；
当p<0时，方程没有实数根．1 对于任意实数x，多项式x2－2x＋3的值一定是(　　)
A．非负数 B．正数
C．负数 D．无法确定练一练2　若x2＋6x＋m2是一个完全平方式，则m的值是(　　)
A．3 B．－3 C．±3 D．以上都不对
3　若方程4x2－(m－2)x＋1＝0的左边是一个完全平方式，则m等于(　　)
A．－2 B．－2或6
C．－2或－6 D．2或－6 (1) 2x2+4x-3=0 (2) 3x2-8x-3=0（1）解：方程两边同除以2，得x2+2x-3/2=0移项，得 x2+2x=3/2方程两边都加上1，得x2+2x+1=5/2即：(x+1)2=5/2例6 用配方法解下列一元二次方程例题讲解（2）解：方程两边同除以3，得x2-8/3x-1=0移项，得 x2-8/3x=1方程两边都加上16/9，得x2-8/3x+16/9=25/9即：（x-4/3)2=25/9∴x- 4/3= 5/3 或x- 4/3=- 5/3 ∴x1= 3 或x2= -1/3 例题讲解 (1) 2x2+4x-3=0 (2) 3x2-8x-3=0例6 用配方法解下列一元二次方程4x2+8(n+1)x+16n
=4[x2+2(n+1)x]+16n
=4[x2+2(n+1)x+(n+1)2]-4(n+1)2+16n.
已知4x2+8(n+1)x+16n是一个完全平方式，
则-4(n+1)2+16n = 0. 化简，得 n2 -2n+1=0,
即(n-1)2=0，
解得n1 = n2=1.
所以常数n的值为1例7已知4x2+8(n+1)x+16n是一个关于x的完全平方式，求常数n的值.解：例题讲解(1)配方，得x2－4x＋(－2)2＝－2＋(－2)2，
即(x－2)2＝2，
由此可得x－2＝± ，
∴x1＝ ＋2，x2＝－ ＋2.1(1)x2－4x＋2＝0；　　　(2)6x2－x－12＝0；　　　(3)(x＋2)2－2(x＋2)＝15.解：练一练(2)二次项系数化为1，得x2－ x－2＝0.
移项，得x2－ x＝2.
配方，得x2－ x＋ ＝2＋ ，
即
由此可得
∴x1＝ ，x2＝－ .(2)6x2－x－12＝0；　解：练一练(3)配方，得(x＋2)2－2(x＋2)＋1＝16，
即(x＋2－1)2＝16，
由此可得x＋1＝±4，
∴x1＝3，x2＝－5.(3)(x＋2)2－2(x＋2)＝15.解：练一练求代数式的最小值，先将代数式配方成a(x＋m)2＋n的
形式，然后根据完全平方的非负性求代数式的最小值．导引：当x取何值时，代数式2x2－6x＋7的值最小？并求出这个最小值．12x2－6x＋7＝2(x2－3x)＋7
即当x＝ 时，2x2－6x＋7的值最小，最小值为 .解：拓展训练 代数式ax2＋bx＋c(a≠0)配方成a(x＋m)2＋n后，
若a>0，则当x＝－m时，代数式取最小值n；若a<0，
则当x＝－m时，代数式取最大值n.总结归纳用配方法解一元二次方程的步骤是:
(1)如果一元二次方程的二次项系数a不是1就应该先在方程的
两边同时除以a,使方程的二次项系数化为1；
(2)移项，使方程左边只含有二次项和一次项，右边为常数项；
(3)配方，根据完全平方公式的是中的一半的平方,在方程的两
边各加上一次项系数一半的平方,可使方程的左边变成一个
完全平方式,右边是一个常数的形式；
(4)解变形后的一元二次方程:如果右边是非负实数,就用直接开
平方法解一元二次方程.如果右边是负实数,则原方程无实数
根即原方程无解．课堂小结用配方法解一元二次方程的基本步骤：ax2+bx+c=0
4.用开平方法将方程两边开平方。课堂小结5.求出原方程的两个解。★一除、二移、三配、四开、五解.完成教材P33-P34作业题T1，T3-T6，
教材P35作业题T1-T5课后作业谢谢