2.2.4 公式法 课件

课件27张PPT。第二章 一元二次方程 一元二次方程根的判别式2.2 一元二次方程的解法2.2.4 公式法 刘谦的魔术表演风靡全国，小林也学起了刘谦
发明了一个魔术盒，当任意实数对(a，b)进入其中时，
会得到一个新的实数：a2+b-1，例如把(3，-2)放入
其中，就会得到32+(-2)-1=6．现将实数对(m，-2m)
放入其中，得到实数2，你知道m的值是多少吗？课时导入（2）开平方法本节课将学习第四种方法：（4）公式法（1）因式分解法2、一元二次方程的解法：复习回顾（3）配方法 下面我们来探讨怎样用配方法解用一般形式表示
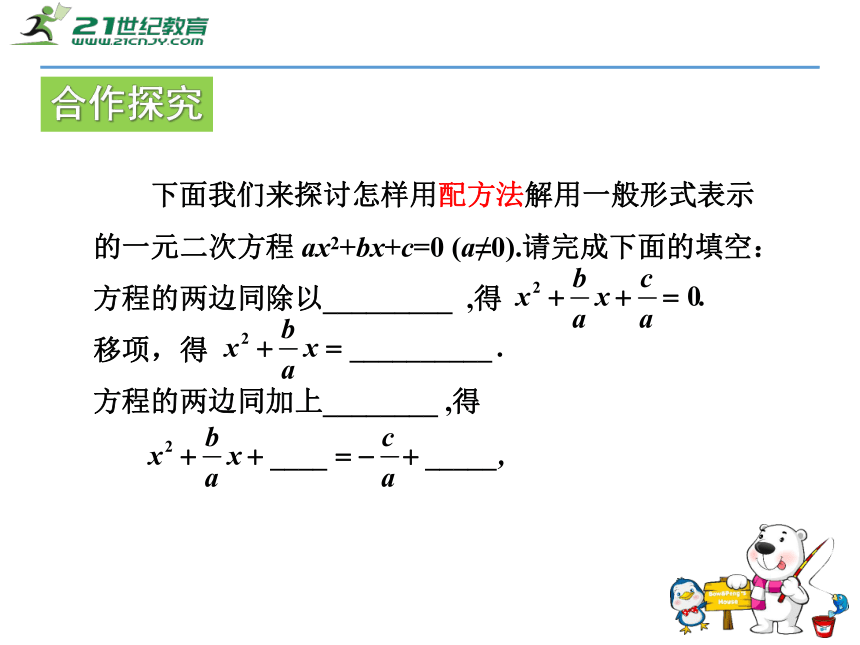
的一元二次方程 ax2+bx+c=0 (a≠0).请完成下面的填空：
方程的两边同除以_________ ,得
移项，得
方程的两边同加上________ ,得合作探究即
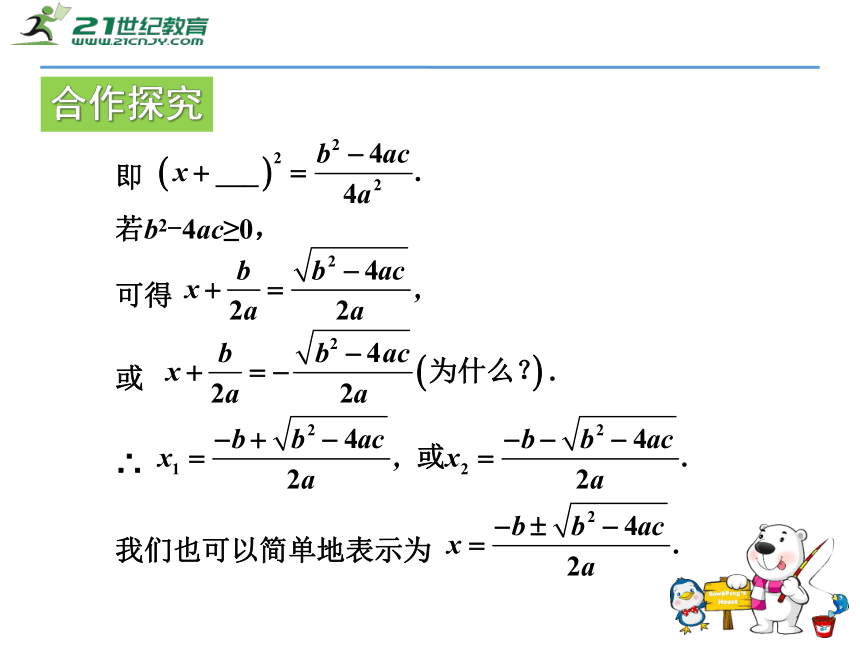
若b2-4ac≥0，
可得
或
∴
我们也可以简单地表示为合作探究 对于一元二次方程ax2+bx+c=0 (a≠0)，如果
b2-4ac≥0，那么方程的 两个根为
这个公式叫做一元二次方程的求根公式.总结归纳 用求根公式解一元二次方程的方法叫做公式法．由求根公式知，一元二次方程最多有两个实根．(1)此求根公式专指一元二次方程的求根公式，只有当
能确认方程是一元二次方程时，方可使用．
(2)是一元二次方程求根公式的重要组成部分，是公式
成立的前提条件．
(3)由求根公式可知，一元二次方程的根不可能多于两个.
(4)求根公式表达了用配方法解一元二次方程
ax2+bx+c=0,(a≠0) 的结果.
(5)对于任意的一元二次方程只要化成一般形式后，满足
b2-4ac≥0的条件，都可以用公式法来解答，这种方法
是解方程的万能公式.定义拓展 先把方程整理变形为一般式，然后确定方程中a、
b、c的值.
(1)方程x2-3x+4=2x2+x-1整理，得x2+4x-5=0.
所以a=1,b=4,c=-5.
(2)方程(x-3)2=4(x+1)整理，得x2-10x+5=0.
a=1,b=-10,c=5.1 指出下列方程中a、b、c的值.
(1) x2-3x+4=2x2+x-1;(2)(x-3)2=4(x+1)分析：解：做一做 指出二次项系数、一次项系数、常数项，首
先要化为一般式， 需要指出的是系数都带着前边
的符号，这是易错点.总结练习1　把方程(2x-3)2-4=2x+3中，b2-4ac的值是（ ）
A.60 B.196
C.164 D.无法确定(1)对方程2x2－5x ＋ 3＝0，
a＝2,b＝－5 , c＝3,
b2－4ac＝(－5)2－4×2 ×3=1,例8 用公式法解下列方程：
(1)2x2－5x ＋ 3＝0； (2)4x2＋1＝ －4x
(3) 解：例题讲解(2)移项，得4x2＋4x ＋1＝0，
a＝4, b＝4, c＝1,
b2－4ac＝42－4×4 ×1=0,(2)4x2＋1＝ －4x解：例题讲解(3)方程的两边同乘4，得3x2－8x－2＝0，
a＝3, b＝－8, c＝－2,
b2－4ac＝(－8)2－4×3×(－2)=88,解：例题讲解用求根公式（公式法）解一元二次方程的一般步骤：
(1)把一元二次方程化成一般形式；
(2)确定公式中a，b，c的值；
(3)求出b2－4ac的值；
(4)若b2－4ac≥0，则把a，b及b2－4ac的值代入求根
公式求解，当b2－4ac＜0时，方程无实数解．总结归纳例9 解：去括号，得
化简，得
则a＝ , b＝－3, c＝4,
b2－4ac＝(－3)2－4× ×4=1,例题讲解总结归纳 例9考查的是用公式法解一元二次方程的能力，
及一元二次方程有根的条件，一元二次有根必须满
足b2-4ac≥0，抓住这个关键此题就迎刃而解了. 我们发现：从一元二次方程ax2+bx+c=0 (a≠0)的求根公式的推导过程中，方程的根的情况由代数式 b2-4ac 的值来决定，因此 b2-4ac 叫做一元二次方程的根的判别式.
根的判别式通常用希腊字母Δ表示，即 Δ= b2-4ac.总结归纳即 一元二次方程的根的个数的判断方法：
(1)当Δ＞0时，方程ax2＋bx＋c＝0(a≠0)有两个不相
等的实数根；
(2)当Δ＝0时，方程ax2＋bx＋c＝0(a≠0)有两个相等
的实数根；
(3)当Δ＜0时，方程ax2＋bx＋c＝0(a≠0)无实数根．Δ= b2-4ac 的值与一元二次方程的根的关系式：求下列一元二次方程的根的判别式的值．
(1) － x2－x＝1；　(2)x2 ＝－ x－ .1根的判别式是在一元二次方程的一般形式下确定
的，因此应先将方程化成一般形式，然后算出根
的判别式的值．导引：(1)原方程化为 x2＋x＋1＝0，Δ＝12－4×1× ＝0.
(2)原方程化为x2 ＋ x＋ ＝0，
Δ＝( )2－4×1× ＝解：做一做2 关于x的一元二次方程x2－(k＋2)x＋2k＝0的根的情况是(　　)
A．有两个不相等的实根　　B．总有实根
C．有两个相等的实根 D．没有实根导引：判别一元二次方程根的情况，主要看根的判别式
与零的大小关系．
∵Δ＝(k＋2)2－4×2k＝k2＋4k＋4－8k
＝k2－4k＋4＝(k－2)2≥0，
∴方程总有实根．B做一做1. 求一元二次方程的根的判别式时应注意两点：
一是将方程化成一般形式后才能确定a，b，c的值；
二是确定a，b，c的值时不要漏掉符号．总结归纳 2. 当根的判别式Δ为一个完全平方式时，方程有实
数根；当Δ为一个完全平方式加一个正数时，方程有
两个不相等的实数根；当Δ为一个完全平方式的相反
数加一个负数时，方程没有实数根．课堂练习1. 用公式法解下列方程．
(1) 2x2+4x-1=0 (2) (3)5x-3=3x2 用公式法解一元二次方程，首先把它化为一般形式，
然后代入公式即可．分析：(1)a=2，b=4，c=-1
△=b2-4ac= 42-4×2×(-1)=24>0
解：(2)a=2，b= ，c=1
△=b2-4ac= ( )2-4×2×1=0
(3) 整理得3x2 -5x+3=0
a=3，b= -5 ，c=3
△=b2-4ac= 25-4×3×3= -11＜0
∴此方程无实根. 课堂练习2. k取何值时，关于x的一元二次方程kx2－12x＋9＝0有两个不相等的实数根？导引：已知方程有两个不相等的实数根，则该方程的
Δ＞0，用含k的代数式表示出Δ，然后列出以k
为未知数的不等式，求出k的取值范围．课堂练习解：∵方程kx2－12x＋9＝0是关于x的一元二次方程，
∴k≠0.方程根的判别式Δ＝(－12)2－4k×9
＝144－36k.
由144－36k＞0，求得k＜4，又 k≠0，
∴当k＜4且k≠0时，方程有两个不相等的实数根．中考链接根据一元二次方程算出b2－4ac的值，根据b2－4ac的
值判断根的情况．b2－4ac＝(－5)2－4×2×3＝1＞0，
所以方程有两个不相等的实数根．故选A.1 〈中考·重庆〉已知一元二次方程2x2－5x＋3＝0，则
该方程根的情况是(　　)
A．有两个不相等的实数根　
B．有两个相等的实数根　
C．两个根都是自然数　
D．无实数根导引：A2〈中考·凉山州〉关于x的一元二次方程(m－2)x2＋
2x＋1＝0有实数根，则m的取值范围是(　　)
A. m≤3　　　　　　　 B．m＜3
C．m＜3且m≠2 D．m≤3且m≠2导引：根据一元二次方程有实数根，可知方程根的判别式
大于或等于零，从而建立关于m的不等式，再求
解即可．因为一元二次方程有实数根，所以Δ≥0，
即4－4(m－2)≥0，解得m≤3，又因为方程为一元二
次方程，所以m－2≠0，即m≠2，故选D.D中考链接用公式法解一元二次方程的“四个步骤”：
(1)把一元二次方程化为一般形式；
(2)确定a，b，c的值；
(3)计算b2－4ac的值；
(4)当b2－4ac≥0时，把a，b，c的值代入求根公式，
求出方程的两个实数根；
当b2－4ac<0时，方程无实数根．课堂小结　判断方程根的情况的方法：
①若一元二次方程ax2＋bx＋c＝0(a≠0)的左边是一个
完全平方式，右边是零，则该方程有两个相等的实数根；
②若方程中a，c异号，或b≠0且c＝0时，则该方程有
两个不相等的实数根；
③当方程中a，c同号，必须通过Δ的符号来判断根的情况．课堂小结方程有两个不相等的实数根，说明两点：
一是该方程是一元二次方程，即二次项系数不为零；
二是该方程的Δ＞0.完成教材P38课内练习T3（1）、（2），
教材P38-P39作业题T2-T4，T6课后作业谢谢