3.1 投影 同步练习(含答案)
图片预览




文档简介
3.1
投影
同步练习
一、单选题
1、正午时分,水平放置的正方形在地面上的投影是( )
A、正方形
B、长方形
C、平行四边形
D、菱形
2、下列命题是假命题的是()
A、中心投影下,物高与影长成正比
B、平移不改变图形的形状和大小
C、三角形的中位线平行于第三边
D、圆的切线垂直于过切点的半径
3、下列各种现象属于中心投影现象的是(
)
A、上午10点时,走在路上的人的影子
B、晚上10点时,走在路灯下的人的影子
C、中午用来乘凉的树影
D、升国旗时,地上旗杆的影子
4、在一个晴朗的天气里,小颖在向正北方向走路时,发现自己的身影向左偏,你知道小颖当时所处的时间是( )
A、上午
B、中午
C、下午
D、无法确定
5、当你乘车沿一条平坦大道向前方行驶时,你会发现,前方那些高一些的建筑物好像“沉”到了位于他们前面矮一些的那些建筑物后面去了,这是因为(
)
A、汽车的速度很快
B、盲区增大
C、汽车的速度很慢
D、盲区减小
6、小刚走路时发现自己的影子越走越长,这是因为( )
A、从路灯下走开,离路灯越来越远
B、走到路灯下,离路灯越来越近
C、人与路灯的距离与影子长短无关
D、路灯的灯光越来越亮
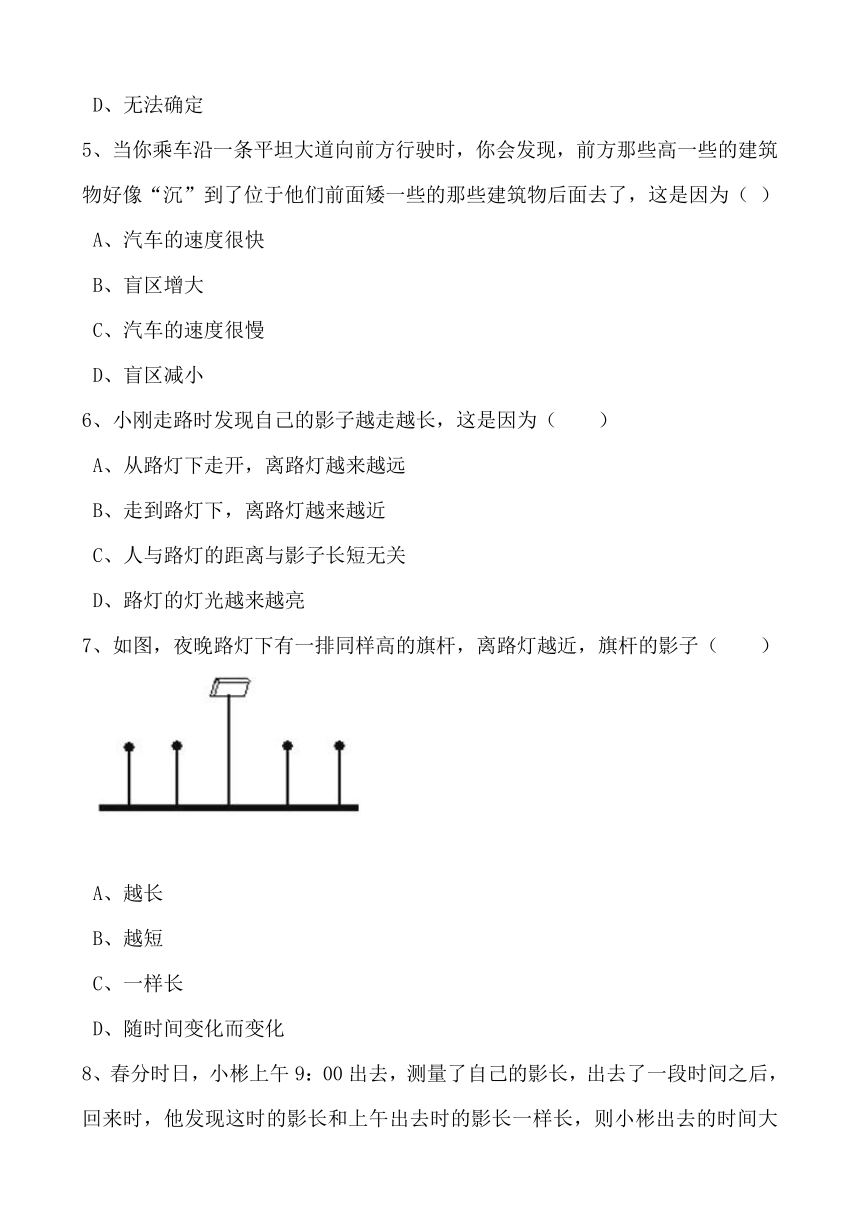
7、如图,夜晚路灯下有一排同样高的旗杆,离路灯越近,旗杆的影子( )
A、越长
B、越短
C、一样长
D、随时间变化而变化
8、春分时日,小彬上午9:00出去,测量了自己的影长,出去了一段时间之后,回来时,他发现这时的影长和上午出去时的影长一样长,则小彬出去的时间大约是( )小时.
A、2
B、4
C、6
D、8
9、(2016 南宁)把一个正六棱柱如图1摆放,光线由上向下照射此正六棱柱时的正投影是(
)
A、
B、
C、
D、
10、下列为某两个物体的投影,其中是在太阳光下形成投影的是( )
A、
B、
C、
D、
11、太阳光线与地面成60°的角,照射在地面上的一个皮球上,皮球在地面上的投射影长是10,
则皮球的直径是( )
A、5cm
B、15cm
C、10cm
D、8cm
12、如图,从小区的某栋楼的A,B,C,D四个位置向对面楼方向看,所看到的范围的大小顺序是( )
A、A>B>C>D
B、D>C>B>A
C、C>D>B>A
D、B>A>D>C
13、(2016 永州)圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )
A、0.324πm2
B、0.288πm2
C、1.08πm2
D、0.72πm2
14、如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程S之间的变化关系用图象刻画出来,大致图象是( )
A、
B、
C、
D、
二、填空题
15、物体在光线的照射下,会在地面或墙壁上留下它的影子,这就是________ 现象.举例________ 、________ .
16、人无论在太阳光照射下,还是在路灯光照射下都会形成影子,那么影子的长短随时间的变化而变化的是________,影子的长短随人的位置的变化而变化的是________.
17、四个直立在地面上的字母广告牌在不同情况下,在地面上的投影(阴影部分)效果如图,则在字母“L”、“K”、“C”的投影中,与字母“N”属同一种投影的有________ .
18、如图,当太阳光与地面上的树影成45°角时,树影投射在墙上的影高CD等于2米,若树根到墙的距离BC等于8米,则树高AB等于________ 米.
19、(2016 北京)如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为________m.
三、综合题
20、如图,小亮利用所学的数学知识测量某旗杆AB的高度.
(1)请你根据小亮在阳光下的投影,画出旗杆AB在阳光下的投影.
(2)已知小亮的身高为1.72m,在同一时刻测得小亮和旗杆AB的投影长分别为0.86m和6m,求旗杆AB的高.
四、解答题
21、已知如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=2m.
(1)请你画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为4m,请你计算DE的长.
22、如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度.
23、如图,在一间黑屋里用一白炽灯照射一个球,
(1)球在地面上的阴影是什么形状?
(2)当把白炽灯向上移时,阴影的大小会怎样变化?
(3)若白炽灯到球心距离为1米,到地面的距离是3米,球的半径是0.2米,求球在地面上阴影的面积是多少?
24、如图,S为一个点光源,照射在底面半径和高都为2m的圆锥体上,在地面上形成的影子为EB,且∠SBA=30°.(以下计算结果都保留根号)
(1)求影子EB的长;
(2)若∠SAC=60°,求光源S离开地面的高度.
答案部分
一、单选题
1、
【答案】A
2、
【答案】A
3、
【答案】B
4、
【答案】A
5、
【答案】B
6、
【答案】A
7、
【答案】B
8、
【答案】C
9、
【答案】A
10、
【答案】D
11、
【答案】B
12、
【答案】A
13、
【答案】D
14、
【答案】C
二、填空题
15、
【答案】投影 ①窗户的影子 ②遮阳伞的影子
16、
【答案】太阳光下形成的影子;灯光下形成的影子
17、
【答案】K
18、
【答案】10
【考点】平行投影
19、
【答案】3
三、综合题
20、
【答案】
(1)如图所示:
(2)如图,因为DE,AB都垂直于地面,且光线DF∥AC,
所以Rt△DEF∽Rt△ABC,
所以=,
即=,
所以AB=12(m).
答:旗杆AB的高为12m.
四、解答题
21、
【答案】解:(1)如图,EF为此时DE在阳光下的投影;
(2)∵AC∥DF,
∴∠ACB=∠DFE,
∴Rt△ABC∽Rt△DEF,
∴,
即,
解得DE=10(m),
即DE的长为10m.
22、
【答案】解:∵CD∥AB,
∴△EAB∽△ECD,
∴=,即=①,
∵FG∥AB,
∴△HFG∽△HAB,
∴=,即=②,
由①②得=,
解得BD=7.5,
∴=,解得:AB=7.
答:路灯杆AB的高度为7m.
23、
【答案】解:(1)因为球在灯光的正下方,所以阴影是圆形;
(2)白炽灯向上移时,阴影会逐渐变小;
(3)设球在地面上阴影的半径为x米,
则,
解得:x2=,
则S阴影=π平方米.
24、
【答案】解:(1)∵圆锥的底面半径和高都为2m,
∴CH=HE=2m,
∵∠SBA=30°,
∴HB=2m,
∴影长BE=BH﹣HE=2﹣2(m);
(2)作CD⊥SA于点D,
在Rt△ACD中,
得CD=ACcos30°=AC=,
∵∠SBA=30°,∠SAB=∠SAC+∠BAC=60°+45°=105°,
∴∠DSC=45°,
∴SC==2,
∴SB=2+BC=2+4,
∴SF=SB=(+2)m,
答:光源S离开地面的高度为(2+)m.
投影
同步练习
一、单选题
1、正午时分,水平放置的正方形在地面上的投影是( )
A、正方形
B、长方形
C、平行四边形
D、菱形
2、下列命题是假命题的是()
A、中心投影下,物高与影长成正比
B、平移不改变图形的形状和大小
C、三角形的中位线平行于第三边
D、圆的切线垂直于过切点的半径
3、下列各种现象属于中心投影现象的是(
)
A、上午10点时,走在路上的人的影子
B、晚上10点时,走在路灯下的人的影子
C、中午用来乘凉的树影
D、升国旗时,地上旗杆的影子
4、在一个晴朗的天气里,小颖在向正北方向走路时,发现自己的身影向左偏,你知道小颖当时所处的时间是( )
A、上午
B、中午
C、下午
D、无法确定
5、当你乘车沿一条平坦大道向前方行驶时,你会发现,前方那些高一些的建筑物好像“沉”到了位于他们前面矮一些的那些建筑物后面去了,这是因为(
)
A、汽车的速度很快
B、盲区增大
C、汽车的速度很慢
D、盲区减小
6、小刚走路时发现自己的影子越走越长,这是因为( )
A、从路灯下走开,离路灯越来越远
B、走到路灯下,离路灯越来越近
C、人与路灯的距离与影子长短无关
D、路灯的灯光越来越亮
7、如图,夜晚路灯下有一排同样高的旗杆,离路灯越近,旗杆的影子( )
A、越长
B、越短
C、一样长
D、随时间变化而变化
8、春分时日,小彬上午9:00出去,测量了自己的影长,出去了一段时间之后,回来时,他发现这时的影长和上午出去时的影长一样长,则小彬出去的时间大约是( )小时.
A、2
B、4
C、6
D、8
9、(2016 南宁)把一个正六棱柱如图1摆放,光线由上向下照射此正六棱柱时的正投影是(
)
A、
B、
C、
D、
10、下列为某两个物体的投影,其中是在太阳光下形成投影的是( )
A、
B、
C、
D、
11、太阳光线与地面成60°的角,照射在地面上的一个皮球上,皮球在地面上的投射影长是10,
则皮球的直径是( )
A、5cm
B、15cm
C、10cm
D、8cm
12、如图,从小区的某栋楼的A,B,C,D四个位置向对面楼方向看,所看到的范围的大小顺序是( )
A、A>B>C>D
B、D>C>B>A
C、C>D>B>A
D、B>A>D>C
13、(2016 永州)圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )
A、0.324πm2
B、0.288πm2
C、1.08πm2
D、0.72πm2
14、如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程S之间的变化关系用图象刻画出来,大致图象是( )
A、
B、
C、
D、
二、填空题
15、物体在光线的照射下,会在地面或墙壁上留下它的影子,这就是________ 现象.举例________ 、________ .
16、人无论在太阳光照射下,还是在路灯光照射下都会形成影子,那么影子的长短随时间的变化而变化的是________,影子的长短随人的位置的变化而变化的是________.
17、四个直立在地面上的字母广告牌在不同情况下,在地面上的投影(阴影部分)效果如图,则在字母“L”、“K”、“C”的投影中,与字母“N”属同一种投影的有________ .
18、如图,当太阳光与地面上的树影成45°角时,树影投射在墙上的影高CD等于2米,若树根到墙的距离BC等于8米,则树高AB等于________ 米.
19、(2016 北京)如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为________m.
三、综合题
20、如图,小亮利用所学的数学知识测量某旗杆AB的高度.
(1)请你根据小亮在阳光下的投影,画出旗杆AB在阳光下的投影.
(2)已知小亮的身高为1.72m,在同一时刻测得小亮和旗杆AB的投影长分别为0.86m和6m,求旗杆AB的高.
四、解答题
21、已知如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=2m.
(1)请你画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为4m,请你计算DE的长.
22、如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度.
23、如图,在一间黑屋里用一白炽灯照射一个球,
(1)球在地面上的阴影是什么形状?
(2)当把白炽灯向上移时,阴影的大小会怎样变化?
(3)若白炽灯到球心距离为1米,到地面的距离是3米,球的半径是0.2米,求球在地面上阴影的面积是多少?
24、如图,S为一个点光源,照射在底面半径和高都为2m的圆锥体上,在地面上形成的影子为EB,且∠SBA=30°.(以下计算结果都保留根号)
(1)求影子EB的长;
(2)若∠SAC=60°,求光源S离开地面的高度.
答案部分
一、单选题
1、
【答案】A
2、
【答案】A
3、
【答案】B
4、
【答案】A
5、
【答案】B
6、
【答案】A
7、
【答案】B
8、
【答案】C
9、
【答案】A
10、
【答案】D
11、
【答案】B
12、
【答案】A
13、
【答案】D
14、
【答案】C
二、填空题
15、
【答案】投影 ①窗户的影子 ②遮阳伞的影子
16、
【答案】太阳光下形成的影子;灯光下形成的影子
17、
【答案】K
18、
【答案】10
【考点】平行投影
19、
【答案】3
三、综合题
20、
【答案】
(1)如图所示:
(2)如图,因为DE,AB都垂直于地面,且光线DF∥AC,
所以Rt△DEF∽Rt△ABC,
所以=,
即=,
所以AB=12(m).
答:旗杆AB的高为12m.
四、解答题
21、
【答案】解:(1)如图,EF为此时DE在阳光下的投影;
(2)∵AC∥DF,
∴∠ACB=∠DFE,
∴Rt△ABC∽Rt△DEF,
∴,
即,
解得DE=10(m),
即DE的长为10m.
22、
【答案】解:∵CD∥AB,
∴△EAB∽△ECD,
∴=,即=①,
∵FG∥AB,
∴△HFG∽△HAB,
∴=,即=②,
由①②得=,
解得BD=7.5,
∴=,解得:AB=7.
答:路灯杆AB的高度为7m.
23、
【答案】解:(1)因为球在灯光的正下方,所以阴影是圆形;
(2)白炽灯向上移时,阴影会逐渐变小;
(3)设球在地面上阴影的半径为x米,
则,
解得:x2=,
则S阴影=π平方米.
24、
【答案】解:(1)∵圆锥的底面半径和高都为2m,
∴CH=HE=2m,
∵∠SBA=30°,
∴HB=2m,
∴影长BE=BH﹣HE=2﹣2(m);
(2)作CD⊥SA于点D,
在Rt△ACD中,
得CD=ACcos30°=AC=,
∵∠SBA=30°,∠SAB=∠SAC+∠BAC=60°+45°=105°,
∴∠DSC=45°,
∴SC==2,
∴SB=2+BC=2+4,
∴SF=SB=(+2)m,
答:光源S离开地面的高度为(2+)m.
