5.1.2矩形 课件(共17张PPT)
文档属性
| 名称 | 5.1.2矩形 课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 564.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-03 16:26:52 | ||
图片预览




文档简介
课件17张PPT。
5.1 矩形(2)自主导学1、有一个角是直角的平行四边形叫做矩形(定义)
有三个角是直角的四边形是矩形(矩形的判定定理1)
对角线相等的平行四边形是矩形(矩形的判定定理2)
2、C
3、(1)(4)(7)错;其他都对
2、要判定一个四边形是矩形只要说明几个角是直角?为什么?ABCD矩形的判定定理1:有三个角是直角的四边形是矩形.几何语言: ∵∠A=∠B=∠C=90°,
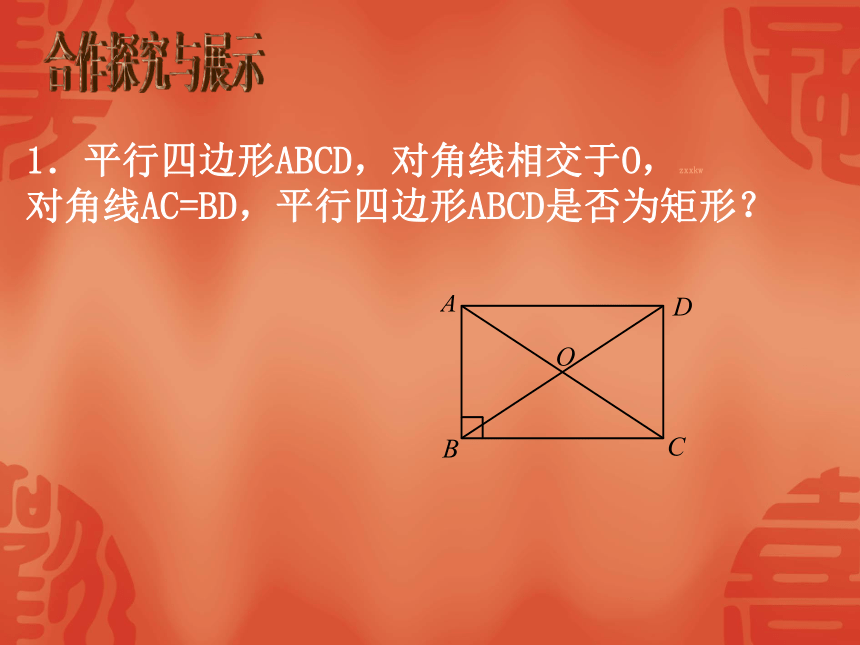
∴四边形ABCD是矩形1、命题“矩形的四个角都是直角”的逆命题是什么?请大家自己进行证明逆命题:四个角都是直角的四边形是矩形。真命题合作探究与展示1.平行四边形ABCD,对角线相交于O,zxxkw
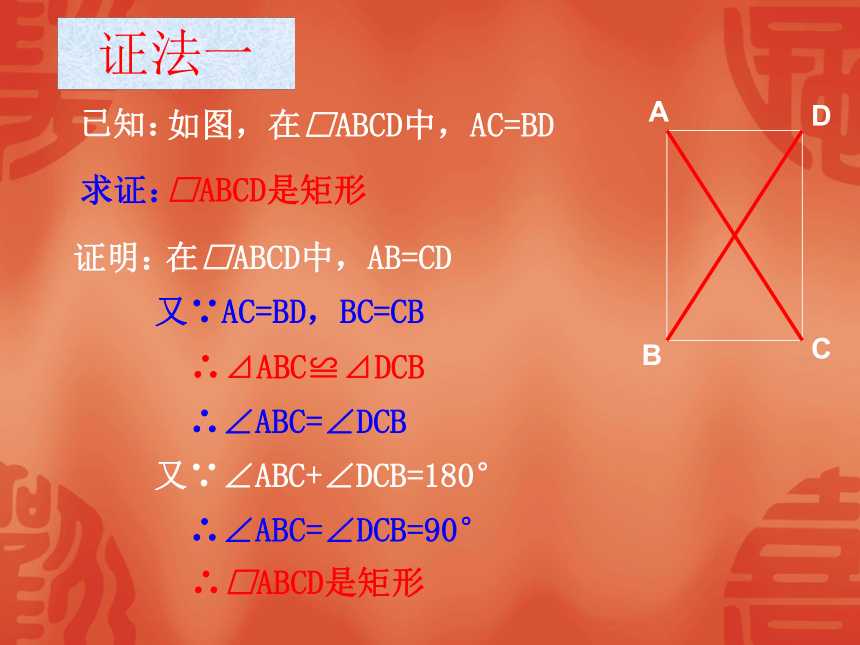
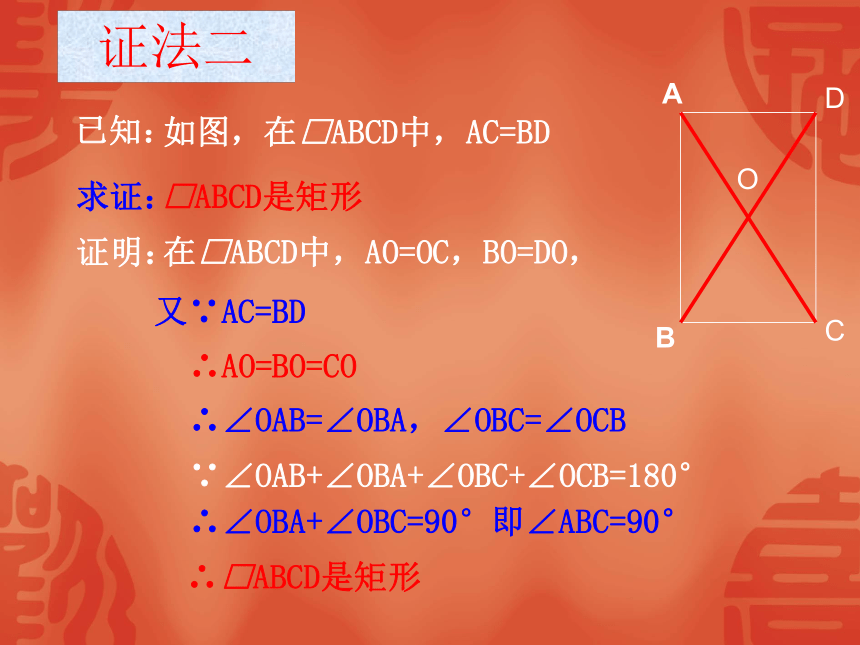
对角线AC=BD,平行四边形ABCD是否为矩形?证法一ABCD证明: 在□ABCD中,AB=CD 又∵AC=BD,BC=CB ∴⊿ABC≌⊿DCB ∴∠ABC=∠DCB 又∵∠ABC+∠DCB=180° ∴∠ABC=∠DCB=90° ∴□ABCD是矩形 已知: 如图,在□ABCD中,AC=BD求证: □ABCD是矩形ABCDO在□ABCD中,AO=OC,BO=DO, 证明: 又∵AC=BD∴AO=BO=CO ∴∠OAB=∠OBA,∠OBC=∠OCB ∵∠OAB+∠OBA+∠OBC+∠OCB=180° ∴∠OBA+∠OBC=90°即∠ABC=90° ∴□ABCD是矩形证法二已知: 如图,在□ABCD中,AC=BD求证: □ABCD是矩形ABCD矩形的判定定理2:对角线相等的平行四边形是矩形;几何语言: ∵AC=BD ∴□ ABCD是矩形矩形有几种判定方法?有一个角是直角的平行四边形叫做矩形(定义)
有三个角是直角的四边形是矩形(矩形的判定定理1)
对角线相等的平行四边形是矩形(矩形的判定定理2)矩形有一个角是直角对角线相等有三个角是直角方法总结:2. 已知:如图,四边形ABCD的对角线AC与BD相交于点O,且AC⊥BD。E、F、G、H分别是AB、BC、CD、AD的中点。求证:四边形EFGH是矩形合作探究与展示课堂检测1、B
2、300,600
3、4、证明: 在矩形ABCD中, AC=BD ,
AO=CO=BO=DO∵AE=CG=BF=DH ∴ OE=OG=OF=OH, EG=FH ∴四边形EFGH是平行四边形∴四边形EFGH是矩形5、略[问题]一张四边形纸板ABCD形状如图,
(1)若要从这张纸板中剪出一个平行四边形,并且使它的四个顶点分别落在四边形ABCD的四条边上,可怎样剪?EFGH⑵四边形ABCD满足什么情况下中点四边形EFGH为矩形?并说明理由.解:分别取AB,BC,CD,DA的中点E,F,G,H,可剪得中点四边形EFGH为平行四边形.两条对角线互相垂直,AC⊥BD例2、一张四边形的纸板ABCD的形状如图(1),它的两条对角线互相垂直。如果要从这张纸板中剪出一个矩形,并且使它的四个顶点分别落在四边形ABCD的四条边上,可以怎么剪?解:EFGH理由如下:∵GH是⊿ACD的中位线∴GH∥AC123∵AC⊥BD∴∠1=90°(三角形的中位线平行于第三边
且等于第三边的一半)∴∠2=∠1=90°∵EH是⊿ABD的中位线∴EH∥BD∴∠3=∠2=90°,45(三角形的中位线平行于第三边)同理可得:∠4=90°, ∠5=90°∴四边形EFGH是矩形.(三个角是直角的四边形是矩形)矩形与平行四边形的性质对比两对角线相等且互相平分两条对角线互相平分对角线对角相等,都是90°对角相等角两组对边平行且相等两组对边平行且相等边矩形平行四边形性质如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线的长. 4如图: 矩形ABCD沿着AE折叠,使D点落在边BC上的F点处,
如果∠BAF=60°, ∠EAF=60则等于 ( )(A) 15°见再
5.1 矩形(2)自主导学1、有一个角是直角的平行四边形叫做矩形(定义)
有三个角是直角的四边形是矩形(矩形的判定定理1)
对角线相等的平行四边形是矩形(矩形的判定定理2)
2、C
3、(1)(4)(7)错;其他都对
2、要判定一个四边形是矩形只要说明几个角是直角?为什么?ABCD矩形的判定定理1:有三个角是直角的四边形是矩形.几何语言: ∵∠A=∠B=∠C=90°,
∴四边形ABCD是矩形1、命题“矩形的四个角都是直角”的逆命题是什么?请大家自己进行证明逆命题:四个角都是直角的四边形是矩形。真命题合作探究与展示1.平行四边形ABCD,对角线相交于O,zxxkw
对角线AC=BD,平行四边形ABCD是否为矩形?证法一ABCD证明: 在□ABCD中,AB=CD 又∵AC=BD,BC=CB ∴⊿ABC≌⊿DCB ∴∠ABC=∠DCB 又∵∠ABC+∠DCB=180° ∴∠ABC=∠DCB=90° ∴□ABCD是矩形 已知: 如图,在□ABCD中,AC=BD求证: □ABCD是矩形ABCDO在□ABCD中,AO=OC,BO=DO, 证明: 又∵AC=BD∴AO=BO=CO ∴∠OAB=∠OBA,∠OBC=∠OCB ∵∠OAB+∠OBA+∠OBC+∠OCB=180° ∴∠OBA+∠OBC=90°即∠ABC=90° ∴□ABCD是矩形证法二已知: 如图,在□ABCD中,AC=BD求证: □ABCD是矩形ABCD矩形的判定定理2:对角线相等的平行四边形是矩形;几何语言: ∵AC=BD ∴□ ABCD是矩形矩形有几种判定方法?有一个角是直角的平行四边形叫做矩形(定义)
有三个角是直角的四边形是矩形(矩形的判定定理1)
对角线相等的平行四边形是矩形(矩形的判定定理2)矩形有一个角是直角对角线相等有三个角是直角方法总结:2. 已知:如图,四边形ABCD的对角线AC与BD相交于点O,且AC⊥BD。E、F、G、H分别是AB、BC、CD、AD的中点。求证:四边形EFGH是矩形合作探究与展示课堂检测1、B
2、300,600
3、4、证明: 在矩形ABCD中, AC=BD ,
AO=CO=BO=DO∵AE=CG=BF=DH ∴ OE=OG=OF=OH, EG=FH ∴四边形EFGH是平行四边形∴四边形EFGH是矩形5、略[问题]一张四边形纸板ABCD形状如图,
(1)若要从这张纸板中剪出一个平行四边形,并且使它的四个顶点分别落在四边形ABCD的四条边上,可怎样剪?EFGH⑵四边形ABCD满足什么情况下中点四边形EFGH为矩形?并说明理由.解:分别取AB,BC,CD,DA的中点E,F,G,H,可剪得中点四边形EFGH为平行四边形.两条对角线互相垂直,AC⊥BD例2、一张四边形的纸板ABCD的形状如图(1),它的两条对角线互相垂直。如果要从这张纸板中剪出一个矩形,并且使它的四个顶点分别落在四边形ABCD的四条边上,可以怎么剪?解:EFGH理由如下:∵GH是⊿ACD的中位线∴GH∥AC123∵AC⊥BD∴∠1=90°(三角形的中位线平行于第三边
且等于第三边的一半)∴∠2=∠1=90°∵EH是⊿ABD的中位线∴EH∥BD∴∠3=∠2=90°,45(三角形的中位线平行于第三边)同理可得:∠4=90°, ∠5=90°∴四边形EFGH是矩形.(三个角是直角的四边形是矩形)矩形与平行四边形的性质对比两对角线相等且互相平分两条对角线互相平分对角线对角相等,都是90°对角相等角两组对边平行且相等两组对边平行且相等边矩形平行四边形性质如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线的长. 4如图: 矩形ABCD沿着AE折叠,使D点落在边BC上的F点处,
如果∠BAF=60°, ∠EAF=60则等于 ( )(A) 15°见再
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
