4.1.2多边形（2） 课件

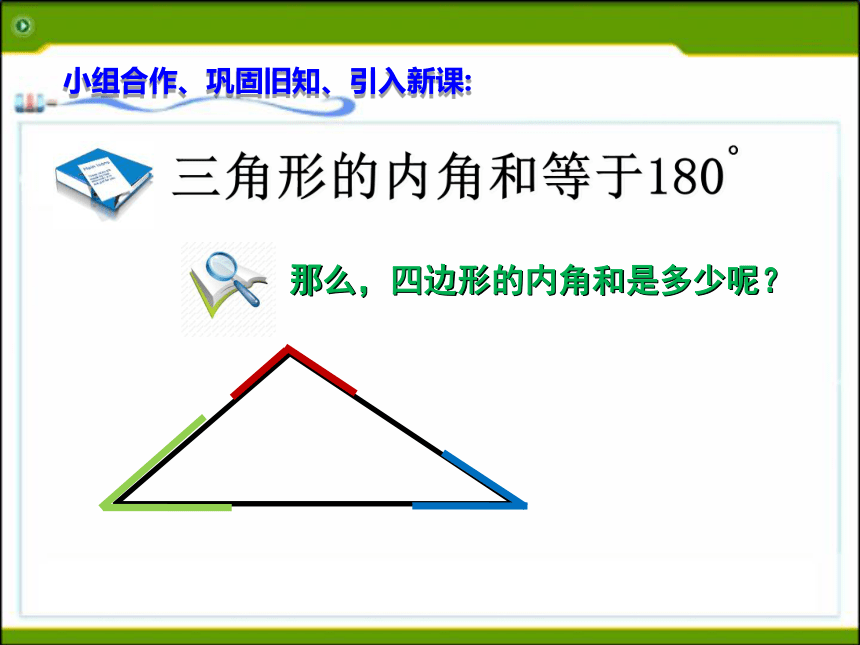
课件26张PPT。新浙教版数学八年级（下）4.1 多边形（2）小组合作、巩固旧知、引入新课: 3个角
（三角形） 4个角
(四边形) 5个角
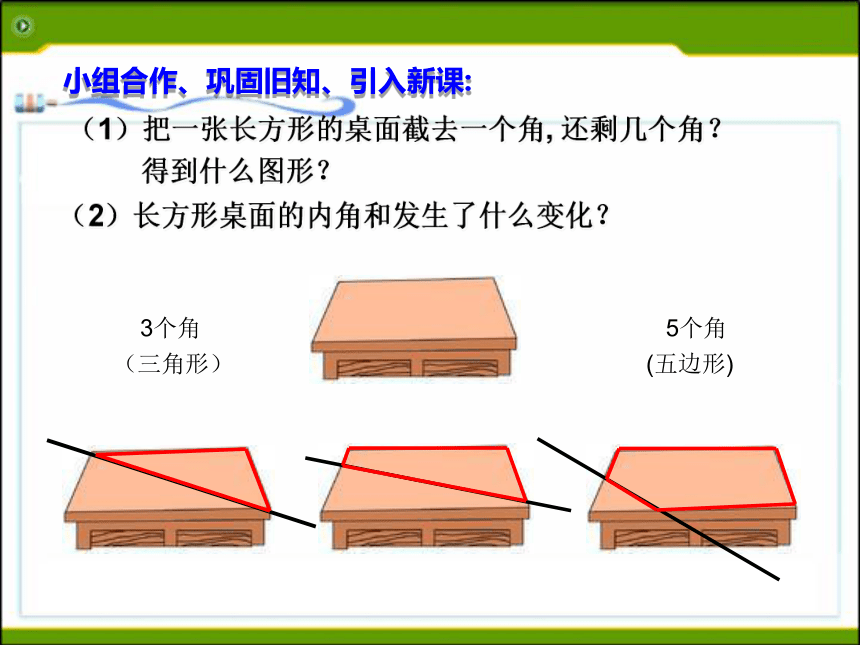
(五边形)（1）把一张长方形的桌面截去一个角, 还剩几个角？
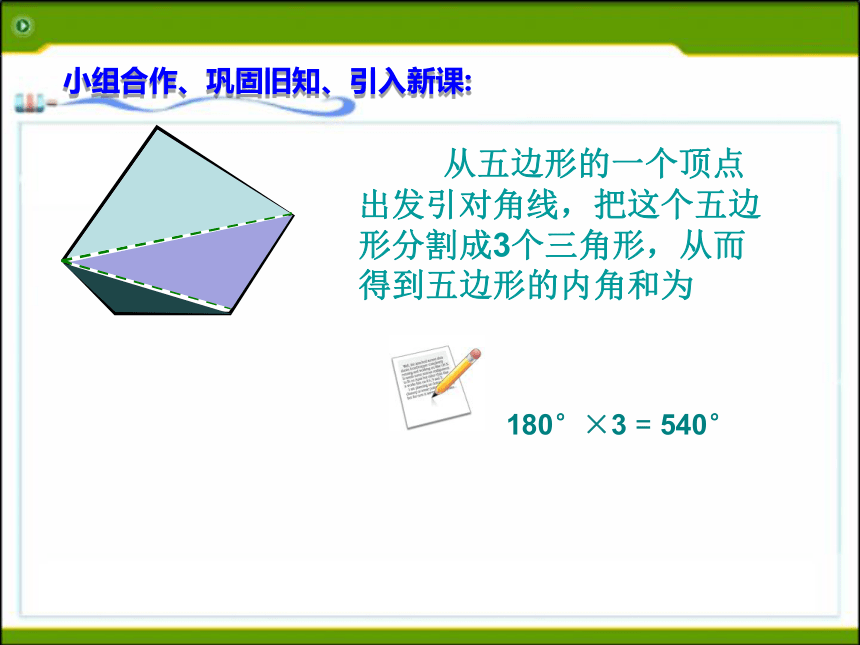
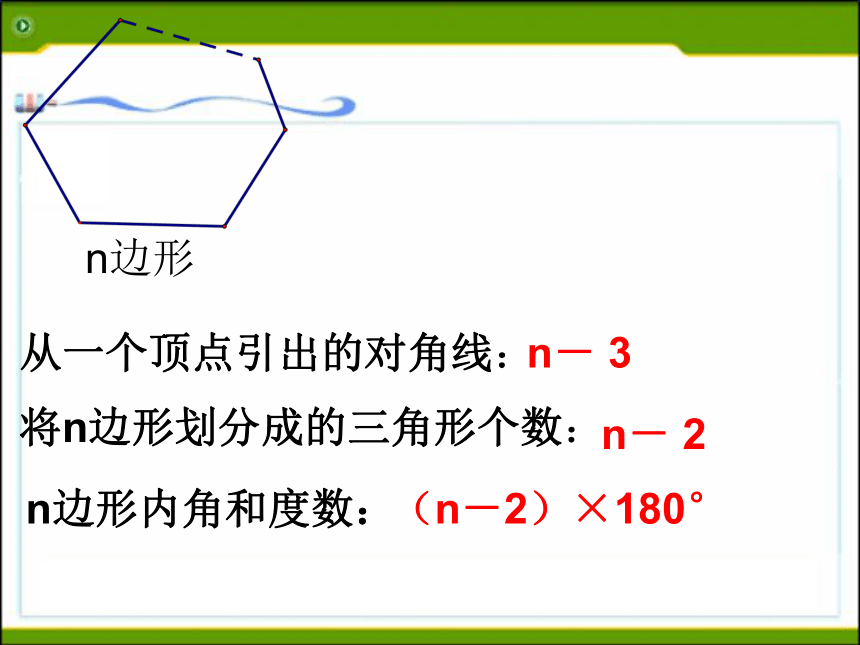
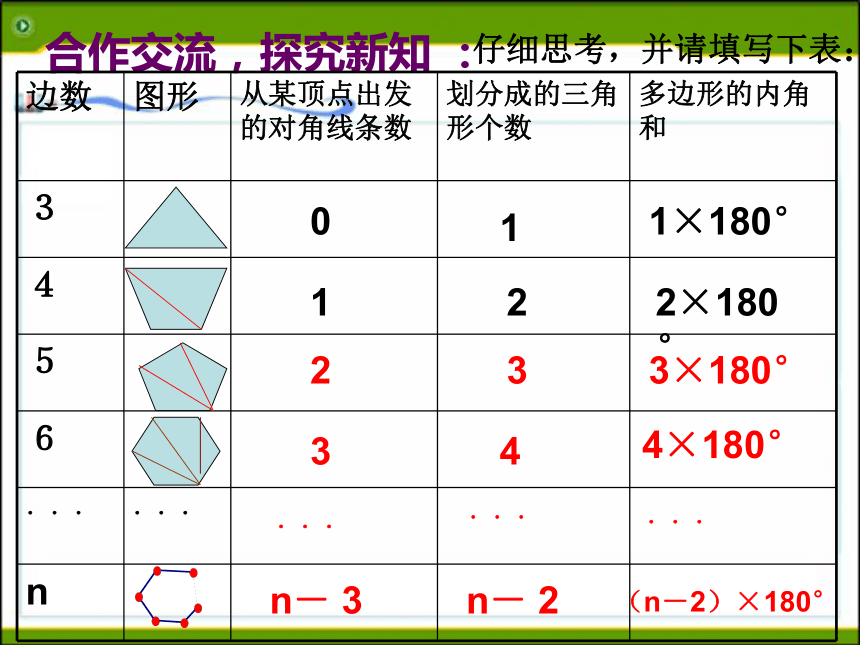
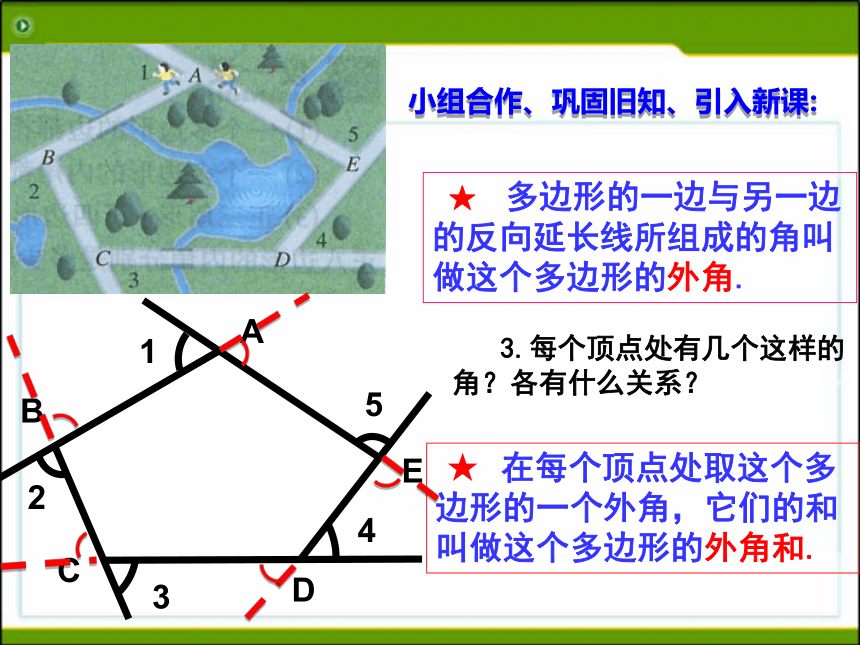
得到什么图形？（2）长方形桌面的内角和发生了什么变化？小组合作、巩固旧知、引入新课: 从五边形的一个顶点出发引对角线，把这个五边形分割成3个三角形，从而得到五边形的内角和为小组合作、巩固旧知、引入新课:①三角形②四边形③五边形④六边形⑤ n边形请画出下列图形的对角线(从一个顶点出发)： n边形从一个顶点引出的对角线：n－ 3将n边形划分成的三角形个数：n－ 2n边形内角和度数：（n－2）×180° 合作交流，探究新知 ：仔细思考，并请填写下表：23343×180°4×180°n－ 3n－ 2（n－2）×180° 011×180° 122×180° ★ 在每个顶点处取这个多边形的一个外角，它们的和叫做这个多边形的外角和. 3.每个顶点处有几个这样的角？各有什么关系？ ★ 多边形的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.小组合作、巩固旧知、引入新课:3×180o-1×180o=360o4×180o-2×180o=360o5×180o-3×180o=360o6×180o-4×180o=360on×180o-(n-2)×180o=360o合作学习多边形的外角和ABCn边形的内角和为（n-2）X 180o （n≥3)任何多边形的外角和为360o结论：2.（a＋1）边形的内角和是________.(a-1)180° (1)八边形的内角和是 ____。
(2)十边形的内角和是____。
(3)一个多边形的内角和是1800°，它是 ________边形。（8－2）×180o=1080o（10－2）×180o=1440o（n－2）×180o=1800o n=12 4、已知一个多边形，它的内角和等于720°，求这个多边形的边数。



解： 设多边形的边数为n，
(n-2)?180°= 720o。
解得: n=6
?这个多边形的边数为6。那么这个多边形的对角线条数为（ ） 例 一个多边形的内角和等于它的外角和的3倍，它是几边形？
解：设这个多边形是n边形，则它的内
角和是（n-2）·1800，外角和等于3600. 由题意得
（n-2）·180=3×360
解得 n=8
答：这个多边形是八边形.（1）求出图中的 x 的值: （2）正十边形内角和是多少？它的 每个内角是多少？课堂练习2、（3）已知一个多边形的每一个外角都是72o，求 这个边形的边数为______ 5如果一个四边形的一组对角互补，那么另一组对角有什么关系？解:因为∠A+∠B+∠C+∠D=360°

所以∠ B+∠D =360°－(∠A+∠C)
=360°－180°
=180°如果四边形一组对角互补，那么另一组对角也互补。
例1、一个六边形如图，已知AB∥DE，BC∥EF，CD∥AF，求∠A＋∠C＋∠E的度数。 ∵AB∥DE， CD∥AF（已知）∴∠1＝∠3，∠2＝∠4
（两直线平行，内错角相等） ∴∠1+∠2＝∠3+∠4，
即∠FAB＝∠CDE，同理∠B＝∠E，∠C＝∠F∴∠FAB＋∠C＋∠E= 1／2 ×720°=360°思考：有没有其它的解法？∵∠FAB+∠ABC+∠BCD+∠CDE＋∠DEF＋∠AFE=（6-2）×180°=720°如图所示：可向两个方向分别延长AB，CD，EF三条边，构成△PQR。∵ DE∥AB
∴∠1=∠R,同理∠2=∠R
∴∠1＝∠2，∴∠CDE=∠FAB同理∠AFE＝∠BCD，∠ABC=∠DEF∴∠FAB＋∠BCD＋∠DEF= 1／2 ×720°=360°解法二：3、如图，OB⊥AB，垂足为B，OC⊥AC，垂足为C,试判断∠A与∠1有什么关系？ 5、已知一个多边形，它的内角和等于五边形的内角和的2倍，求这个多边形的边数。 解： 设多边形的边数为n， (n-2)?180°=2×540o。
解得: n=8
?这个多边形的边数8。1、一个正多边形的每一个内角都等于135°，则这个多边形是几边形？解：设这个多边形是n边形，由题意得
（n－2）×180o=n × 135o
解得：n=8
答：这个多边形是八边形。 1、若一个多边形的内角和等于1080°，则这个多边形的边数是_______。
3、正五边形的每个内角是________。
4、下列角度中，不能成为多边形的内角和的是（ ）
（A）540° （B）580° （C）1800° （D）900°
5、从n边形的一个顶点出发画对角线，最多可以画_____条，这些对角线把n边形分成_____个三角形。8108°Bn-3n-2
3．一个多边形的内角和是1800°， 那么这个
多边形是（ ）
A．五边形 B．八边形
C．十边形 D．十二边形 D
1．一个多边形的每个内角都等于135°，则这个多边形为 边形．
2．内角和等于外角和的多边形是 边形．
3．多边形每个内角都相等，内角和为720°，
则它的每一个外角为 ．
八 四 60° 4．随着多边形的边数n的增加，它的外角和（ ）
A．增加 B．减小 C．不变 D．不定
5．一个多边形每个外角都是60°，这个多边形的
外角和为（ ）
A．180° B．360° C．720° D．1080° DC
在四边形ABCD中，∠D=60°，∠B 比∠A大20°，∠C是∠A的2倍，求∠A，∠B，∠C的大小．∠A =70o ∠B =90o∠C =140on边形的内角和为(n－2) ×180°(n≥3)n边形从一个顶点出发的对角线有(n－3)条(n≥3)任何多边形的外角和为360°结论