6.3反比例函数的应用 同步练习题(含答案)
文档属性
| 名称 | 6.3反比例函数的应用 同步练习题(含答案) | 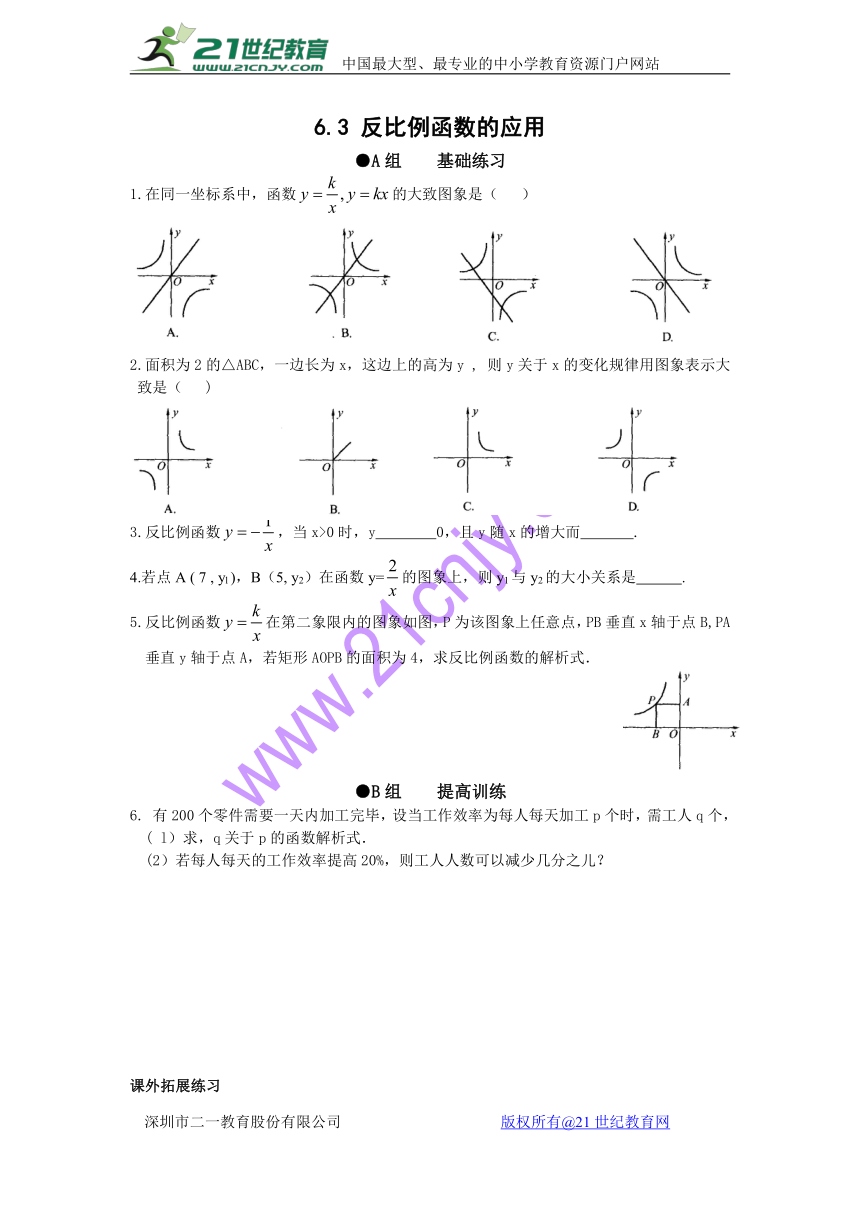 | |
| 格式 | zip | ||
| 文件大小 | 218.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-05 18:49:50 | ||
图片预览

文档简介
6.3 反比例函数的应用
●A组 基础练习
1.在同一坐标系中,函数的大致图象是( )
2.面积为2的△ABC,一边长为x,这边上的高为y , 则y关于x的变化规律用图象表示大致是( )21·cn·jy·com
3.反比例函数,当x>0时,y 0,且y随x的增大而 .
4.若点A ( 7 , yl ),B(5, y2)在函数y=的图象上,则y1与y2的大小关系是 .
5.反比例函数在第二象限内的图象如图,P为该图象上任意点,PB垂直x轴于点B,PA垂直y轴于点A,若矩形AOPB的面积为4,求反比例函数的解析式.
●B组 提高训练
6. 有200个零件需要一天内加工完毕,设当工作效率为每人每天加工p个时,需工人q个,
( l)求,q关于p的函数解析式.
(2)若每人每天的工作效率提高20%,则工人人数可以减少几分之儿?
课外拓展练习
●A组 基础练习
1.已知反比例函数的图象经过点(2, 3), 则当x=-时,函数y的值是( )
A.3 B.-3 C. D.3
2.下列函数中,y随x增大而增大的是( )
A. B.y=-x+3 C. D.
3.一次函数,y=2x-1与反比例函数y=的图象交点个数为 个.
4.写出一个y关于x的反比例函数,使y随x的增大而减小: .
5.如图,A是反比例函数图象上的一点,过A 作x轴的垂线,垂足为点B,当点A在其图象上移动时,△ABO的面积将会发生怎样的变化?对于其他反比例函数,是否也具有相同的现象?21cnjy.com
●B组 提高训练
6.两个反比例函数 y=,y=在第一象限内的图象如图所示,点P1, P2, P3, …, P2005在反比例函数y=图象上,它们的横坐标分别是x1,x2,x3,…,x2005, 纵坐标分别是1, 3,5,…,共2005个连续奇数,过点Pl,P2,P3, …, P2005分别作y轴的平行线,与y=的图象交点依次是Ql (x1, y1) , Q2(x2, y2) , Q3 (x3, y3)…Q2005(x2005, y2005), 则y2005= .21世纪教育网版权所有
7.如图,已知正方形OABC的面积为9,点O为坐标原点,点A在x轴上,点C在y轴上,点B在函数的图象上,点P(m,n) 是函数的图象上任意一点,过点 P分别作x轴,y轴的垂线,垂足分别为E, F,若设矩形OEPF和正方形OABC不重合部分的面积为S. 21教育网
(1)求B点坐标和k的值;
(2)求时点P的坐标;
(3)写出S关于m的函数关系式.
答案:
●A组 基础练习
1.在同一坐标系中,函数的大致图象是( )
2.面积为2的△ABC,一边长为x,这边上的高为y , 则y关于x的变化规律用图象表示大致是( )21·cn·jy·com
3.反比例函数,当x>0时,y 0,且y随x的增大而 .
4.若点A ( 7 , yl ),B(5, y2)在函数y=的图象上,则y1与y2的大小关系是 .
5.反比例函数在第二象限内的图象如图,P为该图象上任意点,PB垂直x轴于点B,PA垂直y轴于点A,若矩形AOPB的面积为4,求反比例函数的解析式.
●B组 提高训练
6. 有200个零件需要一天内加工完毕,设当工作效率为每人每天加工p个时,需工人q个,
( l)求,q关于p的函数解析式.
(2)若每人每天的工作效率提高20%,则工人人数可以减少几分之儿?
课外拓展练习
●A组 基础练习
1.已知反比例函数的图象经过点(2, 3), 则当x=-时,函数y的值是( )
A.3 B.-3 C. D.3
2.下列函数中,y随x增大而增大的是( )
A. B.y=-x+3 C. D.
3.一次函数,y=2x-1与反比例函数y=的图象交点个数为 个.
4.写出一个y关于x的反比例函数,使y随x的增大而减小: .
5.如图,A是反比例函数图象上的一点,过A 作x轴的垂线,垂足为点B,当点A在其图象上移动时,△ABO的面积将会发生怎样的变化?对于其他反比例函数,是否也具有相同的现象?21cnjy.com
●B组 提高训练
6.两个反比例函数 y=,y=在第一象限内的图象如图所示,点P1, P2, P3, …, P2005在反比例函数y=图象上,它们的横坐标分别是x1,x2,x3,…,x2005, 纵坐标分别是1, 3,5,…,共2005个连续奇数,过点Pl,P2,P3, …, P2005分别作y轴的平行线,与y=的图象交点依次是Ql (x1, y1) , Q2(x2, y2) , Q3 (x3, y3)…Q2005(x2005, y2005), 则y2005= .21世纪教育网版权所有
7.如图,已知正方形OABC的面积为9,点O为坐标原点,点A在x轴上,点C在y轴上,点B在函数的图象上,点P(m,n) 是函数的图象上任意一点,过点 P分别作x轴,y轴的垂线,垂足分别为E, F,若设矩形OEPF和正方形OABC不重合部分的面积为S. 21教育网
(1)求B点坐标和k的值;
(2)求时点P的坐标;
(3)写出S关于m的函数关系式.
答案:
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
