2.3 一元二次方程的应用 课件

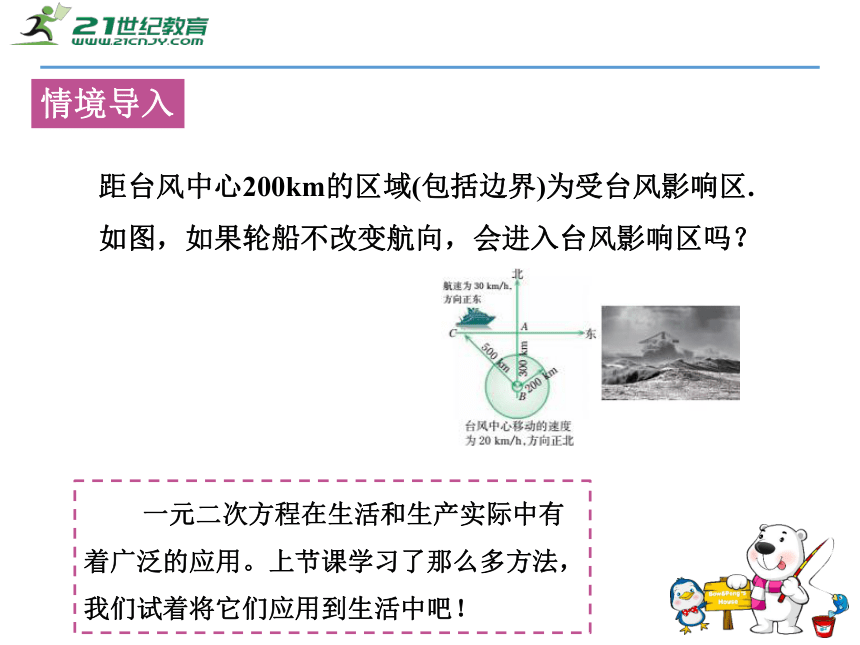
课件26张PPT。第二章 一元二次方程2.3 一元二次方程的应用距台风中心200km的区域(包括边界)为受台风影响区.
如图，如果轮船不改变航向，会进入台风影响区吗？情境导入 一元二次方程在生活和生产实际中有着广泛的应用。上节课学习了那么多方法，我们试着将它们应用到生活中吧！回顾旧知1. 上节课我们学习了解一元二次方程的四种方法：因式分解法开平方法配方法公式法2. 以前我们经历了几次列方程解决应用题？
①列一元一次方程解应用题；
②列二元一次方程组解应用题；
③列分式方程解应用题3. 列一元一次方程解应用题的基本步骤：
①审题：理解题意。②设元（未知数）
③用含未知数的代数式表示相关的量。
④寻找相等关系，列方程。⑤解方程及检验。今天我们将学习另外一种方程解应用题。某花圃用花盆培育某种花苗，经过试验发现，每盆花的盈利与每盆株数构成一定的关系.每盆植入3株时，平均单株盈利3元；以同样的栽培条件，若每盆每增加1株，平均单株盈利就减少0.5元.要使每盆的盈利为10元，则每盆应植多少株？
本题涉及的主要数量有每盆的花苗株数，平均单株
盈利，每盆花苗的盈利.主要数量关系有：
平均单株盈利×株数=每盆盈利；
平均单株盈利=3 -0.5 ×每盆增加的株数.例1分析例题讲解设每盆花苗增加x株，则每盆花苗有(3+x)株，平均
单株盈利为(3-0.5x)元.由题意，得
(x+3) ( 3-0.5x ) = 10.
化简、整理，得x2 -3x+2 = 0.
解这个方程，得x1=1，x2=2.
经检验， x1=1，x2=2都是方程的解，且符合题意.
答:要使每盆的盈利为10元，则每盆应植人4株或5株.解：例题讲解 想一想：列一元二次方程解应用题的基本步骤与一元一次方程解应用题相同吗？列一元二次方程解应用题时，你认为有哪些地方更需引起注意？ 利用方程解应用题的关键是找出等量关系，分析等量关系时，抓住关键词，联想基本关系式，剔除实际背景的文字描述，呈现数学化的形式，列出方程．对解方程得到的根取舍时，要紧扣题意中的每个细节．总结归纳(4)列方程：根据题目中已知量和未知量的关系列出方程．
(5)解方程：利用配方法、公式法、因式分解法等求出未知量的值．
(6)检验：首先检验未知数的值是否满足所列的方程，其次检验它在实际问题中是否有意义．
(7)写出答案：根据题意选择合理的答案．(1)审题：仔细阅读题目，分析题意，明确题目要求，弄清已知数、未知数以及它们之间的关系．
(2)设未知数：一种方法是直接设法，另一种方法是间接设法．
(3)列代数式：用含有未知数x的代数式表示出相关的未知量．列一元二次方程解应用题的一般步骤：总结归纳1. 增长率问题
如果增长率中的基数为a，平均增长率为x，则第
一次增长后的数量为a(1＋x)，第二次增长后的数
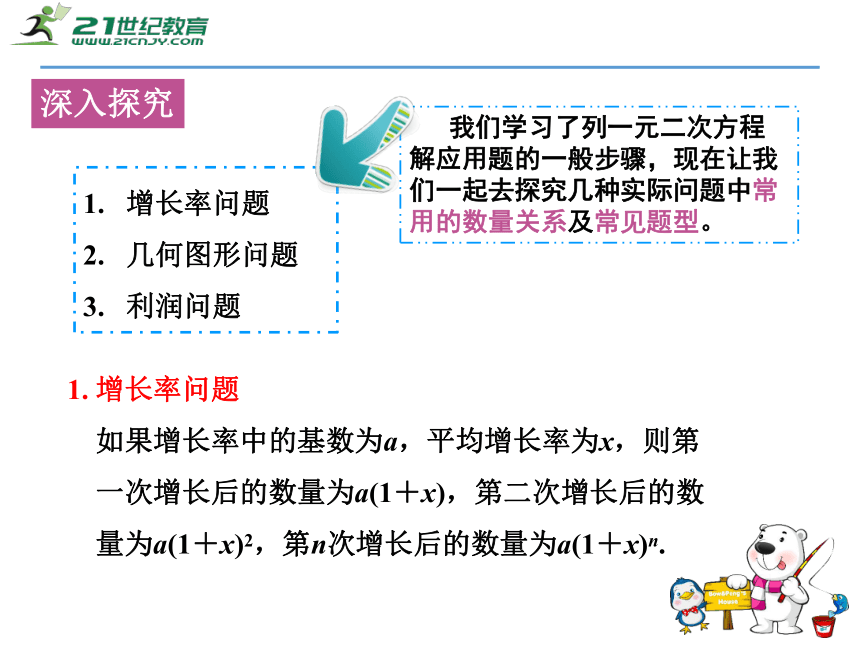
量为a(1＋x)2，第n次增长后的数量为a(1＋x)n.深入探究 我们学习了列一元二次方程解应用题的一般步骤，现在让我们一起去探究几种实际问题中常用的数量关系及常见题型。增长率问题
几何图形问题
利润问题2. 几何图形问题
与几何图形有关的一元二次方程的应用题主要是将数量与数量之间的关系隐藏在图形中，用图形表示出来，这样的图形有三角形、四边形(后面还有圆)，主要涉及图形的周长、面积以及三角形边之间的关系、三角形全等等知识点．深入探究3.利润问题 （单件利润）×（件数） = 利润根据下面的统计图，求从2009年到2011年，我国
风电新增装机容量的平均年增长率(精确到0.1%).例2 例题讲解增长率问题设从2009年到2011年我国风电新增装机容量的
平均年增长率为x，由题意可以列出方程
1380( 1+x)2= 2066.
解这个方程，得解：答：从2009年到2011年，我国风电新增装机容量
的平均年增长率为 22. 4%. 例题讲解平均增长率中的数量关系：
若基数为a，平均增长率为x，则第一次增长后
的数量为a(1＋x)，第二次增长是以a(1＋x)为基
数的，第二次增长后的数量为a(1＋x)2；
若基数是a，平均降低率为x，则第一次降低后
的数量为a(1－x)，第二次降低后的数量为
a(1－x)2.总结归纳如图1，有一张长40 cm，宽25 cm的长方形硬纸
片，裁去角上 四个小正方形之后，折成如图2的
无盖纸盒.若纸盒的底面积是450cm2, 则纸盒的高
是多少？例3 图1图2例题讲解几何图形问题设纸盒的高为x(cm)，那么裁去的四 个小正方形的边长也为x( cm )，这样就可以用关 于x的代数式表示纸盒底面长方形的长和宽.根 据纸盒的底面积是450cm2,就可以列出方程.分析例题讲解设纸盒的高为x(cm)，则纸盒底面长方 形的长和
宽分别为(40-2x)cm，(25-2x)cm.
由题意，得(40-2x)(25-2x) = 450.
化简、整理，得 2x2-65x+275=0.
解这个方程，得
x1 = 5，x2=27.5 (不合题意， 舍去)
答: 纸盒的高为5cm.解 一元二次方程应用题中对于根的取舍，关键是
要体会未知数x所代表的实际意义及限制条件．如
“平均增长率x不能为负”、“小路的宽不能超过
长方形种植地的宽”等这些细节问题都是根取舍的
关键所在．总结归纳利润问题做一做 某商场销售一批名牌衬衫，平均每天可售出20件，每盈利40元。为了扩大销售，增加盈利，尽快减少库存,商场决定采取适当的降价措施。经调查发现，每件衬衫每降价1元，商场平均每天可多售出2件。若商场每天要盈利1200元，请你帮助商场算一算，每件衬衫应降价多少元？可化为一元二次方程的分式方程及其应用为改善生态环境，防止水土流失，某村计划在荒坡上种1000棵树．由于青年志愿者的支援，每天比原计划多种25%，结果提前5天完成任务，原计划每
天种多少棵树？
设原计划每天种树x棵，实际每天植树(1+25%)x棵，
根据实际完成的天数比计划少5天为等量关系建立
方程求出其解即可．分析：拓展训练设原计划每天种树x棵，实际每天植树(1+25%)x棵，
由题意，得
解得：x=40，
经检验，x=40是原方程的解．
答：原计划每天种树40棵．解：拓展训练 本题考查了列分式方程解实际问题的运用，分式方程的解法的运用，工作总量÷工作效率=工作时间在实际问题中的运用，解答时根据实际完成的天数比计划少5天为等量关系建立方程是关键． 一轮船以30 km/h的速度由西向东航行（如图），在途中接到台风警报，台风中心正以20 km/h的速度由南向北移动。已知距台风中心200 km的区域（包括边界）都属于受台风影响区。当轮船接到台风警报时，测得BC=500km，BA=300 km。 ?（1）如果轮船不改变航向，轮船会不会进入台风影响区？你采用什么方法来判断？合作学习C1B1（2）如果你认为轮船会进入台风影响区，那么从接到警报开始，经多少时间就进入台风影响区？（3）如果把航速改为10 Km/h ，结果怎样？ 一轮船以30 km/h的速度由西向东航行（如图），在途中接到台风警报，台风中心正以20 km/h的速度由南向北移动。已知距台风中心200 km的区域（包括边界）都属于受台风影响区。当轮船接到台风警报时，测得BC=500km，BA=300 km。 ?（1）如果轮船不改变航向，轮船会不会进入台风影响区？你采用什么方法来判断？合作学习C1B1（2）如果你认为轮船会进入台风影响区，那么从接到警报开始，经多少时间就进入台风影响区？（3）如果把航速改为10 Km/h ，结果怎样？ 一轮船以30 km/h的速度由西向东航行（如图），在途中接到台风警报，台风中心正以20 km/h的速度由南向北移动。已知距台风中心200 km的区域（包括边界）都属于受台风影响区。当轮船接到台风警报时，测得BC=500km，BA=300 km。 ?（1）如果轮船不改变航向，轮船会不会进入台风影响区？你采用什么方法来判断？AB1C1B合作学习1. 一列火车已晚点6分，如果将速度每小时加快10千米，那么继续行驶20千米便可正点运行．若设这列火车原来行驶的速度是x千米/时，则解决这个问题所列的方程是(　　)
A. B.
C. D.课堂练习 2. 如图，在△ABC中，∠B=90o。点P从点A开始沿边AB向点B以1cm/s的速度移动，与此同时，点Q从点B开始沿边BC向点C以2cm/s的速度移动。如果P、Q分别从A，B同时出发，经过几秒， △ PBQ的面积等于8cm2 ？课堂练习课堂小结注意：列方程解应用题应该注意以下几点：
①要注意应用题中的已知关系和隐藏关系，挖掘出
一个符合题意的等式；
②注意语言与代数式的相互转化，题目中的有些条
件是通过语言描述给出的，要善于从语言中找出
等式；
③要注意单位的统一，单位不统一的，要先统一单
位.课堂小结 完成教材P41-P42作业题T1-T4，
教材P44-P45作业题 T1-T6课后作业谢谢