1.2.2利用三角函数解实际中的方位角、坡角问题课件
文档属性
| 名称 | 1.2.2利用三角函数解实际中的方位角、坡角问题课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-07 18:22:48 | ||
图片预览





文档简介
课件18张PPT。第1章 解直角三角形1.2 锐角三角函数的计算第2课时 利用三角函数解实际中
的方位角、坡角问题1课堂讲解方位角的应用问题
坡角的应用问题2课时流程逐点
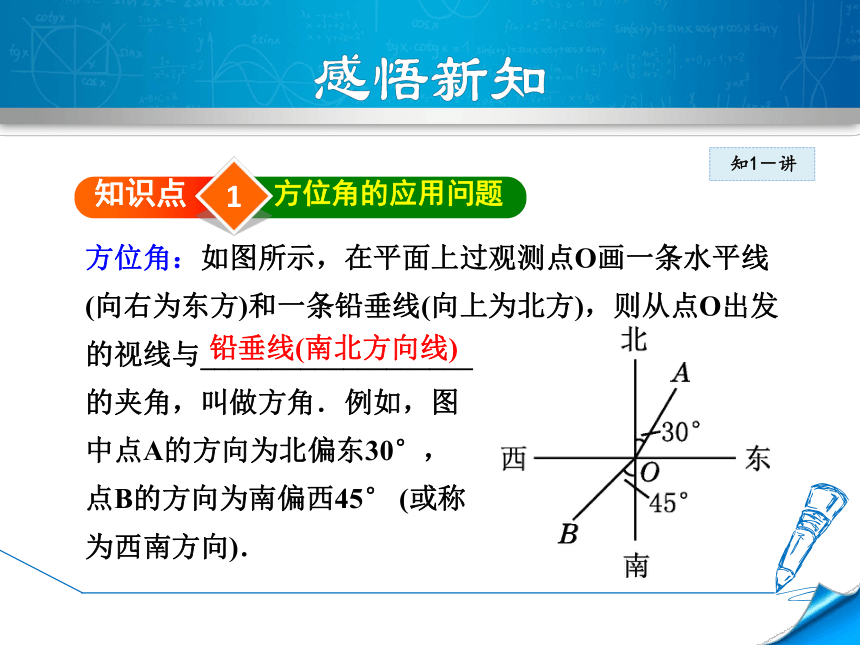
导讲练课堂小结作业提升1知识点方位角的应用问题方位角:如图所示,在平面上过观测点O画一条水平线(向右为东方)和一条铅垂线(向上为北方),则从点O出发的视线与___________________
的夹角,叫做方角.例如,图
中点A的方向为北偏东30°,
点B的方向为南偏西45° (或称
为西南方向).知1-讲铅垂线(南北方向线)例1〈浙江温州〉某海滨浴场东西走向的海岸线可近似看成直线l(如图).
救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处
有人发出求救信号.他立即沿AB方向前往救援,同时通知正在海
岸线上巡逻的救生员乙,乙马上从C处入海,径直向B处游去.甲
在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,
B在C的北偏东35°方向,甲、乙的游泳
速度都是2米/秒.问谁先到达B处?请说
明理由.(参考数据:sin 55°≈0.82,
cos 55°≈0.57,tan 55°≈1.43)知1-讲在Rt△CDB中,利用三角函数即可求得BC,BD的长,
进而分别求得甲、乙到达B处所用的时间,比较二者
的大小即可.知1-讲解析:乙先到达B处.
理由:由题意得∠BCD=55°,∠BDC=90°.
∵tan ∠BCD=
∴BD=CD·tan ∠BCD=40×tan 55°≈57.2(米).
∵cos ∠BCD=
∴BC=
∴t甲≈ t乙≈
∴t甲>t乙.∴乙先到达B处.知1-讲解:总 结知1-讲 解答本题运用了转化思想,即将求时间问题转化
为求线段长度的问题.知1-练(中考·河北)如图,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为( )
A.40海里
B.60海里
C.70海里
D.80海里知1-练如图,一船向正北方向匀速行驶,在C处看见正西
方两座相距10海里的灯塔A和B恰好与该船在同一直
线上,继续航行半小时后,在D处看见灯塔B在南偏
西60°方向上,灯塔A在南偏西75°方向上,则该
船的速度应该是( )海里/小时.
A.10
B.5
C.10
D.5坡比、坡角:
如图所示,坡面的铅垂高度(h)和水平宽度(l)的比叫做坡比,坡面与__________的夹角叫做坡角,记做α.
坡比与坡角的关系是 ,因而坡比越大,坡角α就__________,坡面就越陡.知2-讲水平面越大2知识点坡角的应用问题例2 水库堤坝的横断面是梯形(如图).测得BC长为6m,CD长
为60m,斜坡CD的坡比为1 : 2.5,斜坡AB的坡比为1 : 3.求:
(1) 斜坡CD的坡角∠D和坝底AD的宽(角度精确到1′,宽
度精 确到0.1 m).
(2)若堤坝长150 m,则建造这个堤坝需用多少土石方(精
确到1m3)?知2-讲如上图,作BE⊥AD,CF⊥AD,点E,F为垂足.
在Rt△CFD中,
∴∠D≈21°48′.
∴CF=CD×sinD=60×sin21°48′≈22.28(m),
DF=CD×cosD=60×cos21°48′≈55.71(m).
∵
∴AE=3BE=3CF=66.84(m),
AD=AE+EF+DF=AE+BC+DF
=66.84+6+55.71 = 128.55≈128.6 (m).知2-讲解:(2)横截面的面积
知2-讲需用土石方V=Sl=1498.9×150=224835(m3).答:斜坡CD的坡角约为21°48′,坡底宽约为128.6m,建
造这个大坝需用土石方约为224835m3.总 结知2-讲 解决坡度问题时,可适当天家辅助线,将梯形
分割为直角三角形和矩形来解决问题.知2-练小明沿着与地面成30°角的坡面向下走了2米,那么他下降了( )
A.1米 B. 米 C.2 米 D. 米
2 (14·凉山州)拦水坝横断面如图所示,迎水坡AB的坡
比是1∶ 坝高BC=10 m,则坡面AB的长度是( )
A.15 m B.20 m C.10 m D.20 m知2-练(中考·怀化)如图,小明爬一土坡,他从A处爬到B处
所走的直线距离AB=4米,此时,他离地面高度为
h=2米,则这个土坡的坡角∠A=________°.1.坡角是坡面与水平面间的夹角;坡度(或坡比)是坡面的
铅垂高度与水平长度的比.
2.坡度与坡角的关系是坡度越大,坡角就越大,坡面就越
陡;坡角的正切值等于坡比.
3.解决与方位角有关的实际问题时,必须在每个位置中心
建立方向标,然后根据方位角标出图中已知角的度数,
最后在某个直角三角形内利用锐角三角函数解决问题.1.必做:完成教材P14作业题B组T5,T6,P23
作业题A组T3,B组T5,P25课内练习T2
2.补充: 请完成《典中点》剩余部分习题
的方位角、坡角问题1课堂讲解方位角的应用问题
坡角的应用问题2课时流程逐点
导讲练课堂小结作业提升1知识点方位角的应用问题方位角:如图所示,在平面上过观测点O画一条水平线(向右为东方)和一条铅垂线(向上为北方),则从点O出发的视线与___________________
的夹角,叫做方角.例如,图
中点A的方向为北偏东30°,
点B的方向为南偏西45° (或称
为西南方向).知1-讲铅垂线(南北方向线)例1〈浙江温州〉某海滨浴场东西走向的海岸线可近似看成直线l(如图).
救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处
有人发出求救信号.他立即沿AB方向前往救援,同时通知正在海
岸线上巡逻的救生员乙,乙马上从C处入海,径直向B处游去.甲
在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,
B在C的北偏东35°方向,甲、乙的游泳
速度都是2米/秒.问谁先到达B处?请说
明理由.(参考数据:sin 55°≈0.82,
cos 55°≈0.57,tan 55°≈1.43)知1-讲在Rt△CDB中,利用三角函数即可求得BC,BD的长,
进而分别求得甲、乙到达B处所用的时间,比较二者
的大小即可.知1-讲解析:乙先到达B处.
理由:由题意得∠BCD=55°,∠BDC=90°.
∵tan ∠BCD=
∴BD=CD·tan ∠BCD=40×tan 55°≈57.2(米).
∵cos ∠BCD=
∴BC=
∴t甲≈ t乙≈
∴t甲>t乙.∴乙先到达B处.知1-讲解:总 结知1-讲 解答本题运用了转化思想,即将求时间问题转化
为求线段长度的问题.知1-练(中考·河北)如图,一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为( )
A.40海里
B.60海里
C.70海里
D.80海里知1-练如图,一船向正北方向匀速行驶,在C处看见正西
方两座相距10海里的灯塔A和B恰好与该船在同一直
线上,继续航行半小时后,在D处看见灯塔B在南偏
西60°方向上,灯塔A在南偏西75°方向上,则该
船的速度应该是( )海里/小时.
A.10
B.5
C.10
D.5坡比、坡角:
如图所示,坡面的铅垂高度(h)和水平宽度(l)的比叫做坡比,坡面与__________的夹角叫做坡角,记做α.
坡比与坡角的关系是 ,因而坡比越大,坡角α就__________,坡面就越陡.知2-讲水平面越大2知识点坡角的应用问题例2 水库堤坝的横断面是梯形(如图).测得BC长为6m,CD长
为60m,斜坡CD的坡比为1 : 2.5,斜坡AB的坡比为1 : 3.求:
(1) 斜坡CD的坡角∠D和坝底AD的宽(角度精确到1′,宽
度精 确到0.1 m).
(2)若堤坝长150 m,则建造这个堤坝需用多少土石方(精
确到1m3)?知2-讲如上图,作BE⊥AD,CF⊥AD,点E,F为垂足.
在Rt△CFD中,
∴∠D≈21°48′.
∴CF=CD×sinD=60×sin21°48′≈22.28(m),
DF=CD×cosD=60×cos21°48′≈55.71(m).
∵
∴AE=3BE=3CF=66.84(m),
AD=AE+EF+DF=AE+BC+DF
=66.84+6+55.71 = 128.55≈128.6 (m).知2-讲解:(2)横截面的面积
知2-讲需用土石方V=Sl=1498.9×150=224835(m3).答:斜坡CD的坡角约为21°48′,坡底宽约为128.6m,建
造这个大坝需用土石方约为224835m3.总 结知2-讲 解决坡度问题时,可适当天家辅助线,将梯形
分割为直角三角形和矩形来解决问题.知2-练小明沿着与地面成30°角的坡面向下走了2米,那么他下降了( )
A.1米 B. 米 C.2 米 D. 米
2 (14·凉山州)拦水坝横断面如图所示,迎水坡AB的坡
比是1∶ 坝高BC=10 m,则坡面AB的长度是( )
A.15 m B.20 m C.10 m D.20 m知2-练(中考·怀化)如图,小明爬一土坡,他从A处爬到B处
所走的直线距离AB=4米,此时,他离地面高度为
h=2米,则这个土坡的坡角∠A=________°.1.坡角是坡面与水平面间的夹角;坡度(或坡比)是坡面的
铅垂高度与水平长度的比.
2.坡度与坡角的关系是坡度越大,坡角就越大,坡面就越
陡;坡角的正切值等于坡比.
3.解决与方位角有关的实际问题时,必须在每个位置中心
建立方向标,然后根据方位角标出图中已知角的度数,
最后在某个直角三角形内利用锐角三角函数解决问题.1.必做:完成教材P14作业题B组T5,T6,P23
作业题A组T3,B组T5,P25课内练习T2
2.补充: 请完成《典中点》剩余部分习题
