1.1.3特殊角的三角函数值的计算课件
图片预览






文档简介
课件19张PPT。第1章 解直角三角形1.1 锐角三角函数第3课时 特殊角的三角函数
值的计算1课堂讲解30°、45°、60°角的三角函数值
由特殊三角函数值求角2课时流程逐点
导讲练课堂小结作业提升观察一副三角尺,其中有几个锐角?它们分别等于多少度?
1. sin30°等于多少?你是怎样得到的?与同伴进行交流。
2. cos30°等于多少?tan30°呢?
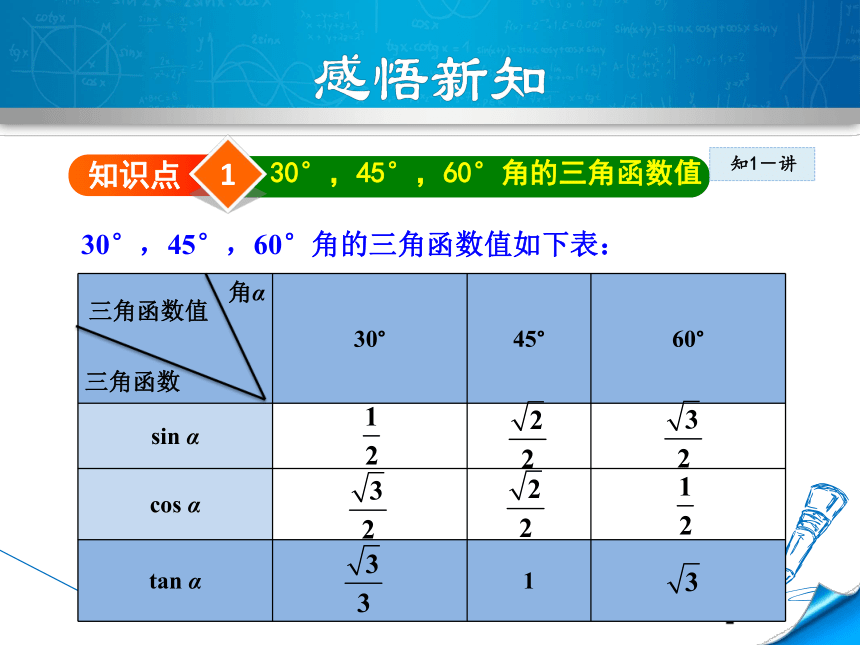
3. 60°角、45°角的三角函数值分别是多少?1知识点30°,45°,60°角的三角函数值 30°,45°,60°角的三角函数值如下表: 知1-讲角α三角函数值三角函数例1 求下列各式的值:
(1)2sin 30°- 3cos 60°.
(2)cos245°+tan 60° ? sin 60°.
(3) cos 30°- sin 45°+tan 45° ? cos 60°.
知1-讲 (1)2sin 30°- 3cos 60°
解: (2)cos245°+tan 60° ? sin 60°.
知1-讲 (2)cos245°+tan 60° ? sin 60°.
(3) cos 30°- sin 45°+tan 45° ? cos 60°.
知1-讲知1-讲 解答此类问题要熟记30°、45°、60°角的三角函
数值,并注意三角函数前的系数。1 计算:
(1) cos 30° ? sin 60°.
(2) sin2 45°—2sin 45°? cos 60°.
(3) sin2 30°+cos2 30°.知1-练(14·包头)计算sin245°+cos30°·tan60°,其结果
是( )
A.2 B.1 C. D.
如图,在Rt△ABC中,∠C=90°,BC= AB,
则sinB=________.知1-练2知识点由特殊三角函数值求角知2-讲在△ABC中,∠A,∠B均为锐角,且sin A=cos B= ,
则下列最确切的结论是( )
A.△ABC是直角三角形
B.△ABC是等腰三角形
C.△ABC是等腰直角三角形
D.△ABC是锐角三角形例2C知2-讲∵∠A,∠B均为锐角,且sin A=cos B= ,
∴∠A=∠B=45°.
∴△ABC是等腰直角三角形.故选C.解析:知2-讲 根据特殊角的三角函数值,直接得出∠A,∠B的
度数,从而得出答案.知2-讲〈贵州贵阳模拟〉如图所示,河岸AD、BC互相平行,桥AB垂直于两岸,从C处看桥的两端A、B,夹角∠BCA=60°,测得BC=7 m,则桥长AB约为________m(结果精确到1 m).
在Rt△ABC中,∠BCA=60°,则tan ∠BCA= ,
其中BC=7 m,则AB=7× =7 ≈12(m).例3解析:12知2-讲 本题运用了转化思想,就是把实际问题转化为直
角三角形中锐角三角函数的有关计算,应熟记特殊角
(30°,45°,60°角)的三角函数值.知2-练在Rt△ABC中,∠C=90°,若sin A= ,则∠B的度数是( )
A.30° B.45° C.60° D.90°在Rt△ABC中,2sin (α+20°)= ,则锐角α
的度数是( )
A.60° B.80°
C.40° D.以上都不对3 若 tan(α+10°)=1,则锐角α的度数是( )
A.20° B.30° C.40° D.50°知2-练4 (2015·庆阳)在△ABC中,若角A,B满足
+(1-tan B)2=0,则∠C的大小
是( )
A.45° B.60° C.75° D.105° 巧记特殊锐角三角函数值的方法:
1. 三角板记忆法:借助如图所示的三角板记忆.
特点记忆法:30°,45°,60°角的正弦值记为
余弦值相反,正切值记为
3. 口诀记忆法:1,2,3;3,2,1;3,9,27;弦比2,
切比3,分子根号别忘添.
1.必做:完成教材P10作业题T1-T6
2.补充: 请完成《典中点》剩余部分习题
值的计算1课堂讲解30°、45°、60°角的三角函数值
由特殊三角函数值求角2课时流程逐点
导讲练课堂小结作业提升观察一副三角尺,其中有几个锐角?它们分别等于多少度?
1. sin30°等于多少?你是怎样得到的?与同伴进行交流。
2. cos30°等于多少?tan30°呢?
3. 60°角、45°角的三角函数值分别是多少?1知识点30°,45°,60°角的三角函数值 30°,45°,60°角的三角函数值如下表: 知1-讲角α三角函数值三角函数例1 求下列各式的值:
(1)2sin 30°- 3cos 60°.
(2)cos245°+tan 60° ? sin 60°.
(3) cos 30°- sin 45°+tan 45° ? cos 60°.
知1-讲 (1)2sin 30°- 3cos 60°
解: (2)cos245°+tan 60° ? sin 60°.
知1-讲 (2)cos245°+tan 60° ? sin 60°.
(3) cos 30°- sin 45°+tan 45° ? cos 60°.
知1-讲知1-讲 解答此类问题要熟记30°、45°、60°角的三角函
数值,并注意三角函数前的系数。1 计算:
(1) cos 30° ? sin 60°.
(2) sin2 45°—2sin 45°? cos 60°.
(3) sin2 30°+cos2 30°.知1-练(14·包头)计算sin245°+cos30°·tan60°,其结果
是( )
A.2 B.1 C. D.
如图,在Rt△ABC中,∠C=90°,BC= AB,
则sinB=________.知1-练2知识点由特殊三角函数值求角知2-讲在△ABC中,∠A,∠B均为锐角,且sin A=cos B= ,
则下列最确切的结论是( )
A.△ABC是直角三角形
B.△ABC是等腰三角形
C.△ABC是等腰直角三角形
D.△ABC是锐角三角形例2C知2-讲∵∠A,∠B均为锐角,且sin A=cos B= ,
∴∠A=∠B=45°.
∴△ABC是等腰直角三角形.故选C.解析:知2-讲 根据特殊角的三角函数值,直接得出∠A,∠B的
度数,从而得出答案.知2-讲〈贵州贵阳模拟〉如图所示,河岸AD、BC互相平行,桥AB垂直于两岸,从C处看桥的两端A、B,夹角∠BCA=60°,测得BC=7 m,则桥长AB约为________m(结果精确到1 m).
在Rt△ABC中,∠BCA=60°,则tan ∠BCA= ,
其中BC=7 m,则AB=7× =7 ≈12(m).例3解析:12知2-讲 本题运用了转化思想,就是把实际问题转化为直
角三角形中锐角三角函数的有关计算,应熟记特殊角
(30°,45°,60°角)的三角函数值.知2-练在Rt△ABC中,∠C=90°,若sin A= ,则∠B的度数是( )
A.30° B.45° C.60° D.90°在Rt△ABC中,2sin (α+20°)= ,则锐角α
的度数是( )
A.60° B.80°
C.40° D.以上都不对3 若 tan(α+10°)=1,则锐角α的度数是( )
A.20° B.30° C.40° D.50°知2-练4 (2015·庆阳)在△ABC中,若角A,B满足
+(1-tan B)2=0,则∠C的大小
是( )
A.45° B.60° C.75° D.105° 巧记特殊锐角三角函数值的方法:
1. 三角板记忆法:借助如图所示的三角板记忆.
特点记忆法:30°,45°,60°角的正弦值记为
余弦值相反,正切值记为
3. 口诀记忆法:1,2,3;3,2,1;3,9,27;弦比2,
切比3,分子根号别忘添.
1.必做:完成教材P10作业题T1-T6
2.补充: 请完成《典中点》剩余部分习题
