1.1.1正弦函数课件
图片预览






文档简介
课件17张PPT。第1章 解直角三角形1.1 锐角三角函数第1课时 正弦函数1课堂讲解正弦函数的定义
正弦函数的应用2课时流程逐点
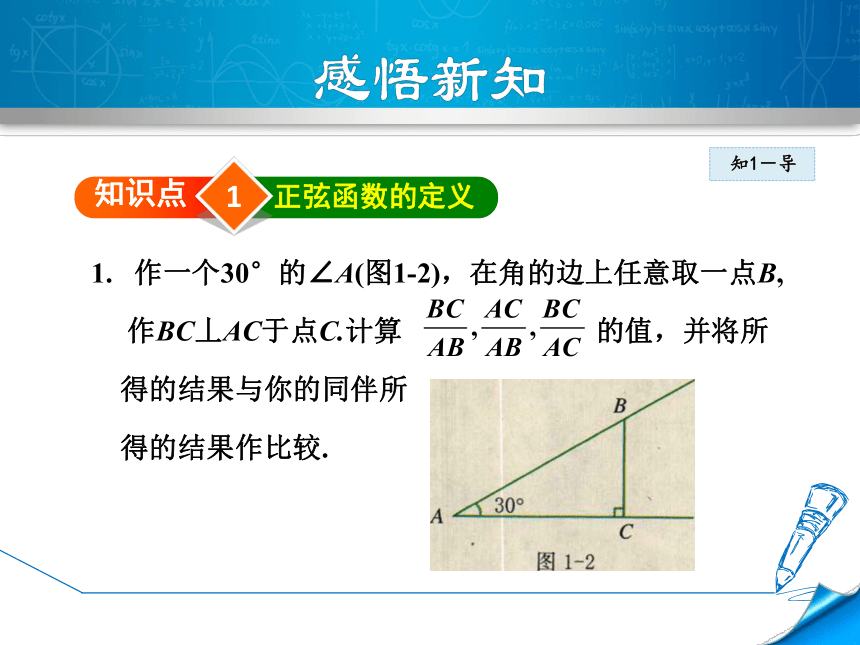
导讲练课堂小结作业提升 如图是两个自动扶梯,甲、乙两人分别从1、2号自动扶梯上楼,谁先到达楼顶?如果AB和A′B′相等而∠α和∠β大小不同,那么它们的高度AC和A′C′相等吗?AB、AC、BC与∠α,A′B′、A′C′、B′C′与∠β之间有什么关系呢?1知识点正弦函数的定义作一个30°的∠A(图1-2),在角的边上任意取一点B,
作BC丄AC于点C.计算 的值,并将所
得的结果与你的同伴所
得的结果作比较.知1-导2. 作一个50°的∠A(图1-3),在角的边上任意取一点B,作
BC丄AC于点C.量出AB , AC,BC的长(精确到1mm),计
算 的值(精确到0.01),
并将所得的结果与你的同
伴所得的结果作比较.
通过上面两个实践操作,
你发现了什么?知1-导知1-导3.如图l-4,B,B1是∠α一边上的任意两点,作BC丄AC于
点C, B1C1丄AC1于点C1判断比值
是否相等,并说明理由.
正弦:如图所示,在 Rt△ABC中,如果锐角∠A确定,那么∠A的对边与斜边的比、邻边与斜边的比、对边与
邻边的比也随之确定.
∠A的对边与________的比叫做∠A的正弦,记做sin A,即 sin A= ,如图所示,sin A=______.知1-讲斜边例1 (浙江温州)如图,在△ABC中,∠C=90°,
AB=5,BC=3,则sin A的值是( )
A. B.
C. D.
解析:∵∠C=90°,AB=5,BC=3,
∴sin A= 知1-讲C知1-讲 本题利用正弦的定义,也就是利用∠A的对边长
比上斜边长直接求解. 例2 如图,在Rt△ABC中,两直角边AC=12,BC=5.求∠A
的正弦函数值.
解:在Rt△ABC中,AC=12,BC=5,∠C=90°,
∴AB=
∴sin A=知1-讲知1-练把Rt△ABC三边的长度都扩大为原来的3倍,则锐
角A的正弦函数值( )
A.不变 B.缩小为原来的
C.扩大为原来的3倍 D.不能确定
(14·贵阳)在Rt△ABC中,∠C=90°,AC=12,
BC =5,则sin A的值为( )
A. B. C. D.知1-练已知Rt△ABC∽Rt△A′B′C′,∠C=∠C′=90°,
且AB=2A′B′,则sinA与sinA′的关系为( )
A.sinA=2sinA′
B.sinA=sinA′
C.2sinA=sinA′
D.不能确定2知识点正弦函数的应用知2-讲 例3 如图,在Rt△ABC中,∠B=90°,AC=200,
sinA=0.6,求BC的长.
解:∵∠B=90°,AC=200,
∴BC=AC×sinA=200×0.6=120.知2-练在△ABC中,AB=AC=5,sin∠ABC=0.8,则BC
=________.
在Rt△ABC中,∠ACB=90°,CD为斜边AB上的
高,若BC=4,sinA= ,则BD的长为______.知2-练3 如图,∠α的顶点为O,它的一边在x轴的正半轴上,
另一边OA上有一点P(b,4),若sin α= ,则b=
________.
求锐角的正弦值的方法:
1.没有直接给出对边或斜边的题目,一般先根据勾
股定理求出所需的边长,再求正弦值.
2.没有给出图形的题目,一般应根据题目,画出符
合题意的图形,弄清所求角的对边与斜边,再求
对边与斜边的比.
3.题目中给出的角不在直角三角形中,应先构造直
角三角形再求解. 1.必做:完成教材P6课内练习T1,
作业题A组T1-T4中求正弦值部分
2.补充: 请完成《典中点》剩余部分习题
正弦函数的应用2课时流程逐点
导讲练课堂小结作业提升 如图是两个自动扶梯,甲、乙两人分别从1、2号自动扶梯上楼,谁先到达楼顶?如果AB和A′B′相等而∠α和∠β大小不同,那么它们的高度AC和A′C′相等吗?AB、AC、BC与∠α,A′B′、A′C′、B′C′与∠β之间有什么关系呢?1知识点正弦函数的定义作一个30°的∠A(图1-2),在角的边上任意取一点B,
作BC丄AC于点C.计算 的值,并将所
得的结果与你的同伴所
得的结果作比较.知1-导2. 作一个50°的∠A(图1-3),在角的边上任意取一点B,作
BC丄AC于点C.量出AB , AC,BC的长(精确到1mm),计
算 的值(精确到0.01),
并将所得的结果与你的同
伴所得的结果作比较.
通过上面两个实践操作,
你发现了什么?知1-导知1-导3.如图l-4,B,B1是∠α一边上的任意两点,作BC丄AC于
点C, B1C1丄AC1于点C1判断比值
是否相等,并说明理由.
正弦:如图所示,在 Rt△ABC中,如果锐角∠A确定,那么∠A的对边与斜边的比、邻边与斜边的比、对边与
邻边的比也随之确定.
∠A的对边与________的比叫做∠A的正弦,记做sin A,即 sin A= ,如图所示,sin A=______.知1-讲斜边例1 (浙江温州)如图,在△ABC中,∠C=90°,
AB=5,BC=3,则sin A的值是( )
A. B.
C. D.
解析:∵∠C=90°,AB=5,BC=3,
∴sin A= 知1-讲C知1-讲 本题利用正弦的定义,也就是利用∠A的对边长
比上斜边长直接求解. 例2 如图,在Rt△ABC中,两直角边AC=12,BC=5.求∠A
的正弦函数值.
解:在Rt△ABC中,AC=12,BC=5,∠C=90°,
∴AB=
∴sin A=知1-讲知1-练把Rt△ABC三边的长度都扩大为原来的3倍,则锐
角A的正弦函数值( )
A.不变 B.缩小为原来的
C.扩大为原来的3倍 D.不能确定
(14·贵阳)在Rt△ABC中,∠C=90°,AC=12,
BC =5,则sin A的值为( )
A. B. C. D.知1-练已知Rt△ABC∽Rt△A′B′C′,∠C=∠C′=90°,
且AB=2A′B′,则sinA与sinA′的关系为( )
A.sinA=2sinA′
B.sinA=sinA′
C.2sinA=sinA′
D.不能确定2知识点正弦函数的应用知2-讲 例3 如图,在Rt△ABC中,∠B=90°,AC=200,
sinA=0.6,求BC的长.
解:∵∠B=90°,AC=200,
∴BC=AC×sinA=200×0.6=120.知2-练在△ABC中,AB=AC=5,sin∠ABC=0.8,则BC
=________.
在Rt△ABC中,∠ACB=90°,CD为斜边AB上的
高,若BC=4,sinA= ,则BD的长为______.知2-练3 如图,∠α的顶点为O,它的一边在x轴的正半轴上,
另一边OA上有一点P(b,4),若sin α= ,则b=
________.
求锐角的正弦值的方法:
1.没有直接给出对边或斜边的题目,一般先根据勾
股定理求出所需的边长,再求正弦值.
2.没有给出图形的题目,一般应根据题目,画出符
合题意的图形,弄清所求角的对边与斜边,再求
对边与斜边的比.
3.题目中给出的角不在直角三角形中,应先构造直
角三角形再求解. 1.必做:完成教材P6课内练习T1,
作业题A组T1-T4中求正弦值部分
2.补充: 请完成《典中点》剩余部分习题
