八年级数学下5.3正方形（2）课件

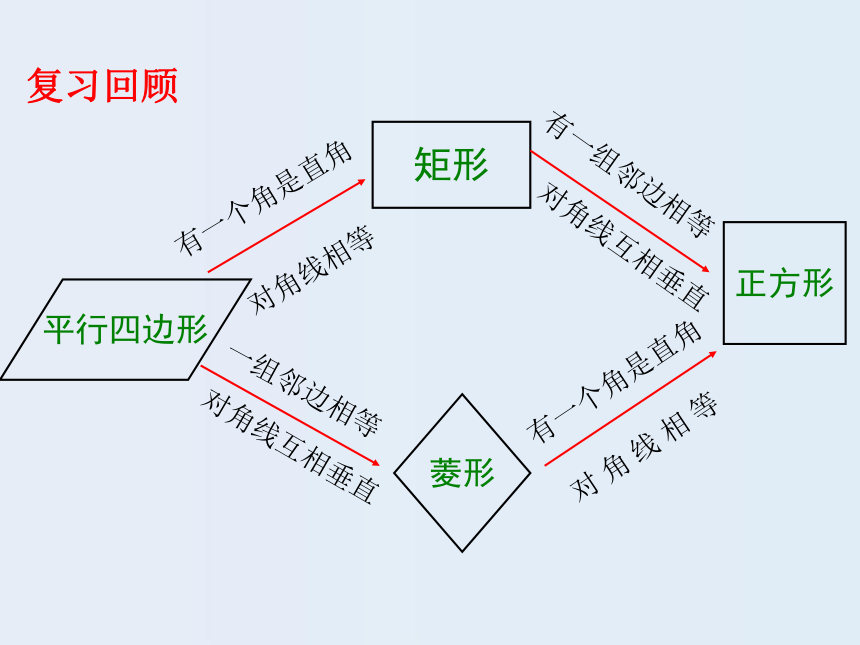
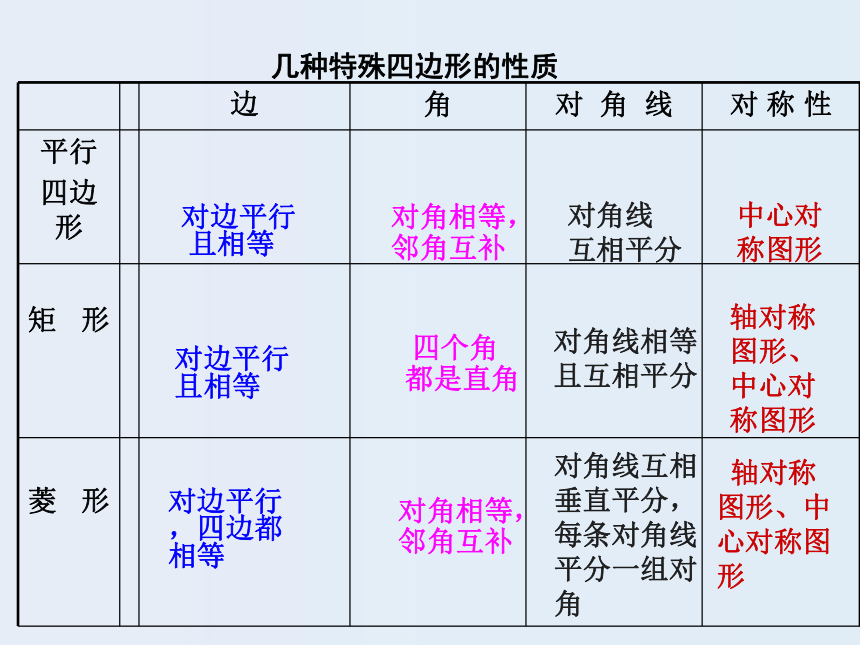
课件12张PPT。5.3正方形（2）平行四边形矩形有一个角是直角正方形有一组邻边相等对角线互相垂直对角线相等菱形一组邻边相等对角线互相垂直有一个角是直角对 角 线 相 等复习回顾 几种特殊四边形的性质 对边平行
且相等对边平行 且相等对边平行
，四边都
相等对角相等，
邻角互补 四个角
都是直角对角相等，邻角互补对角线
互相平分对角线相等
且互相平分对角线互相
垂直平分，
每条对角线
平分一组对角中心对
称图形轴对称
图形、
中心对
称图形 轴对称
图形、中
心对称图形 正方形是特殊的平行四边形，
也是特殊的矩形，也是特殊的菱形。 正方形会有哪些性质呢？正方形的性质请你从对称性、边、角、对角线四个方面进
行考虑，说说正方形有哪些性质吗？正方形4个角都是直角；正方形的两条对角线相等且互
相垂直平分；每一条对角线平
分一组对角从角看：从对角线看：从边看:正方形的四边相等，对边平行；从对称性看：正方形既是轴对称图形，又
是中心对称图形．正方形具有而矩形不一定具有的性质是（ ）
A、四个角相等.
B、对角线互相垂直平分.
C、对角互补.
D、对角线相等.选一选2.正方形具有而菱形不一定具有的性质（ ）
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等. BD例：如图，正方形ABCD中，G是对角线BD上的一点，GE⊥CD,GF⊥BC,求证AG=EF 提示：连接CG,证△ADG≌ △CDG,再由CG=EF,可得AG=EF 1. 如图，分别以△ABC的边AB,AC为一边向外画正方形AEDB和正方形ACFG，连接CE,BG.求证：BG=CE.证明：在正方形ABDE中， AE=AB，∠EAB=90°， 又在正方形ACFG中， AG=AC，∠GAC=90°， ∴∠EAB=∠GAC=90°.∴∠EAC=∠GAB，∴△EAC≌△GAB，
∴EC=GB． ∵∠EAC=∠EAB+∠BAC， ∠GAB=∠GAC+∠BAC，课堂练习2. 正方形ABCD中，E是BC延长线上一点，且CE=AC, AE交DC于点F,试求∠E, ∠AFC的度数解：∵四边形ABCD为正方形，∵CE=AC∴∠E=∠CAE∵∠ACB是⊿ACE的一个外角∴∠ACB=∠E+∠CAE=2∠E∵∠AFC是△CEF的一个外角∴∠AFC=∠E+∠FCE=22.5°+90°=112.5°∴∠E=22.5°, ∠AFC=112.5°jFEABDC3.已知:如图,四边形ABCD与四边形DEFG都是正方形.求证:AE=CG证明：∵四边形ABCD和DEFG都是正方形.
∴DA=DC, DE=DG ,∠ADC=∠EDG
(正方形四条边都相等，四个角都是直角)
∴∠ADC-∠ADG=∠EDG-∠ADG, 即∠GDC=∠EDA在△GDC和△EDA中
DC=DA
∠GDC=∠EDA.
DG=DE
∴△GDC≌△EDA (SAS)
∴AE=CG (全等三角形的对应边相等）4.已知:如图,在正方形ABCD中,E,F分别是BC,CD上的点,
AE⊥BF.?求证:AE＝BF. 证：∵四边形ABCD是正方形,?且AE⊥BF,?∴∠BAE+∠ABF＝90°,?∠ABF+∠FBC＝90°,?∴∠BAE＝∠FBC.?又∵∠ABE＝∠BCF＝90°,AB＝BC,?∴△ABE≌△BCF?∴AE＝BF. 课堂小结正方形的性质：正方形（1）对边平行（2）四边相等（3）四个角都是直角（4）对角线相等互相垂直互相平分平分一组对角边对角线