第2章 直线与圆的位置关系 专题训练(含答案)
文档属性
| 名称 | 第2章 直线与圆的位置关系 专题训练(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 196.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-10 12:52:04 | ||
图片预览



文档简介
第2章
直线与圆的位置关系
专题训练
专项训练一:直线与圆的位置关系
名师点金:直线与圆的位置关系有相离、相切、相交三种情况,考查方向主要体现在:根据已知条件判断直线与圆的位置关系,根据直线与圆的位置关系求值或取值范围,有关直线与圆的位置关系的动态探究等.
根据d与r的大小关系判断直线与圆的位置关系
1.在平面直角坐标系中,以点(2,3)为圆心,2为半径的圆必定( )
A.与x轴相离,与y轴相切
B.与x轴、y轴都相离
C.与x轴相切,与y轴相离
D.与x轴、y轴都相切
2.已知⊙O的半径为2,圆心O到直线AB的距离为d,且方程x2-2x+d=0没有实数根,试确定直线AB与⊙O的位置关系.
根据直线与圆的位置关系求值或取值范围
3.如图,⊙P的半径为2,圆心P是抛物线y=x2-1上的点,当⊙P与x轴相切时,圆心P的坐标为________.
(第3题)
4.如图,直线l与⊙O相交于A,B两点,且与半径OC垂直,垂足为H,已知AB=16
cm,cos
∠OBH=.
(1)求⊙O的半径;
(2)如果要将直线l向下平移到与⊙O相离的位置,平移的距离应满足什么条件?
(第4题)
有关直线与圆的位置关系的动态探究
5.如图①,在四边形ABCD中,∠D=∠C=90°,AB=4,BC=6,AD=8.点P,Q同时从A点出发,分别做匀速运动,其中点P沿AB,BC向终点C运动,速度为每秒2个单位,点Q沿AD向终点D运动,速度为每秒1个单位.当这两点中有一点到达终点时,另一点也停止运动.设这两点运动了t秒.
(第5题)
(1)动点P与Q哪一点先到达终点?此时t为何值?(直接写出结果)
(2)当0<t<2时,求证:以PQ为直径的圆与AD相切(如图②).
(3)以PQ为直径的圆能否与CD相切?若能,求出t的值或取值范围;若不能,请说明理由.
专项训练二:证明切线的技巧
名师点金:有关切线的证明分两种情况:一是直线过圆上某一点,证明直线是圆的切线时,只需“连半径,
证垂直,得切线”;二是直线和圆没有已知的公共点时,
通常“作垂直,证半径,得切线”.
已知半径,证明垂直
1.如图,已知⊙O的半径OB=1,DE是⊙O的直径,过D作⊙O的切线,C是AD的中点,AE交⊙O于点B,四边形BCOE是平行四边形.
(1)求AD的长.
(2)BC是⊙O的切线吗?若是,请给出证明;若不是,请说明理由.
(第1题)
连半径,证垂直
类型1:连一条半径证垂直
2.如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论.
(第2题)
类型2:连两条半径证垂直
3.如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连结AD交BC于点F,若AC=FC.
(1)求证:AC是⊙O的切线;
(2)若BF=8,DF=,求⊙O的半径r.
(第3题)
作垂直,证半径
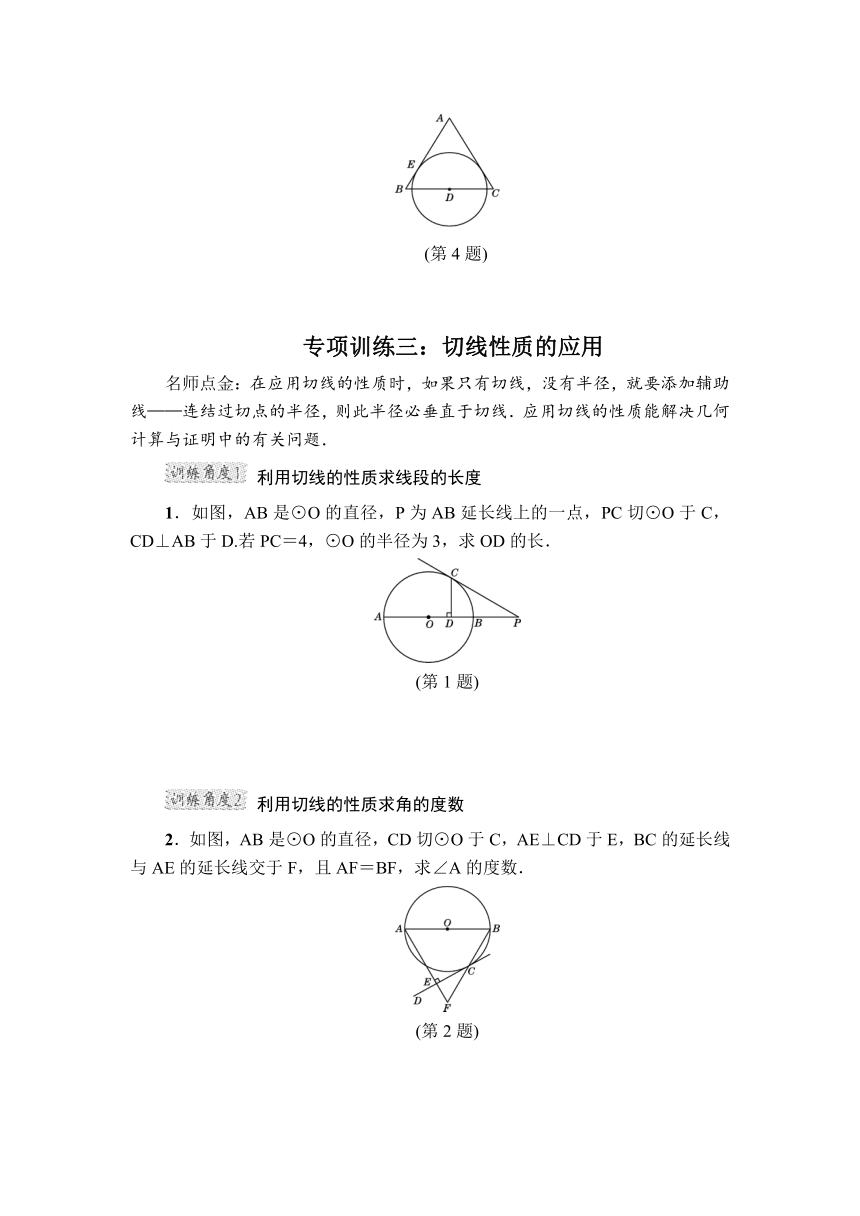
4.如图,AB=AC,D为BC的中点,⊙D与AB切于E点.求证:AC与⊙D相切.
(第4题)
专项训练三:切线性质的应用
名师点金:在应用切线的性质时,如果只有切线,没有半径,就要添加辅助线——连结过切点的半径,则此半径必垂直于切线.应用切线的性质能解决几何计算与证明中的有关问题.
利用切线的性质求线段的长度
1.如图,AB是⊙O的直径,P为AB延长线上的一点,PC切⊙O于C,CD⊥AB于D.若PC=4,⊙O的半径为3,求OD的长.
(第1题)
利用切线的性质求角的度数
2.如图,AB是⊙O的直径,CD切⊙O于C,AE⊥CD于E,BC的延长线与AE的延长线交于F,且AF=BF,求∠A的度数.
(第2题)
利用切线的性质证明线段相等
3.如图,AB是⊙O的直径,CO⊥AB,CD切⊙O于D,AD交CO于E.求证:CD=CE.
(第3题)
利用切线的性质证明角相等
4.如图,AB是⊙O的直径,BD切⊙O于点B,延长AB到C,使BC=OB,过点C作⊙O的切线,E为切点,与BD交于点F,AE的延长线交BD于点D.
求证:∠D=∠DFE.
(第4题)
答案
专项训练一
1.A
2.解:∵方程x2-2x+d=0没有实数根,
∴(-2)2-4d<0,
即d>1.
当1<d<2时,直线AB与⊙O相交;
当d=2时,直线AB与⊙O相切;
当d>2时,直线AB与⊙O相离.
3.(,2)或(-,2)
点拨:当⊙P与x轴相切时,由⊙P的半径为2,且圆的切线垂直于过切点的半径,可得P点纵坐标为2;又P在抛物线y=x2-1上,故将y=2代入得:2=x2-1,解得:x1=,x2=-.
4.解:(1)∵直线l与半径OC垂直,∴HB=AB=×16=8(cm).
∵cos
∠OBH==,∴OB=HB=×8=10(cm),即⊙O的半径为10
cm.
(2)在Rt△OBH中,OH===6(cm).
∴CH=OC-OH=10-6=4(cm).
∴将直线l向下平移到与⊙O相离的位置时,平移的距离必须大于4
cm.
5.(1)解:点P先到达终点,此时t=5.
(2)证明:如图,过点B作BM⊥AD,垂足为M,设圆与AB交于N,易得AM=2.
(第5题)
又∵AB=4,∴∠A=60°.
连结QN,∵PQ为直径,∴∠QNP=90°,∴∠NQA=30°.
∵AQ=t,AP=2t,∴AN=t,∴PN=t,NQ=t,∴PQ==t.
∴AQ2+PQ2=AP2.
∴△APQ为直角三角形,且∠AQP=90°.
∴以PQ为直径的圆与AD相切.
(3)解:能.设圆心为F,作FE⊥CD于E,PH⊥AD于H.∵CP=10-2t,DQ=8-t,∴EF=(CP+DQ)=(18-3t),PQ=2EF=18-3t.
∵PQ2=PH2+HQ2,且PH=AB·sin60°=2,
HQ=(8-t)-(10-2t)=t-2,
∴(t-2)2+(2)2=(18-3t)2.
解得t=或t=(舍去).
故当t=时,以PQ为直径的圆与CD相切.
专项训练二
1.解:(1)连结BD,∵DE是直径,∴∠DBE=∠ABD=90°.
∵四边形BCOE是平行四边形,
∴BC∥OE,BC=OE=1.
在Rt△ABD中,∵C为AD的中点,
∴BC=AD=1,∴AD=2.
(2)是,理由如下:
∵BC∥OD,BC=OD,∴四边形BCDO为平行四边形.
∵AD为⊙O的切线,∴OD⊥AD,
∴四边形BCDO为矩形.∴OB⊥BC.
∴BC是⊙O的切线.
2.(1)证明:连结CD.
∵BC是⊙O的直径,∴CD⊥AB.
又∵BC=AC,∴点D是AB的中点.
(2)解:DE与⊙O相切.证明如下:
连结OD,∵OD=OC,∴∠ODC=∠OCD.
又∵BC=AC,D是AB的中点,
∴∠BCD=∠ACD.
∵DE⊥AC,∴∠ACD+∠CDE=90°,
∴∠ODC+∠CDE=90°,
∴OD⊥DE.又∵OD为⊙O的半径,
∴DE是⊙O的切线.
3.(1)证明:如图,连结OA,OD,则OA=OD,∴∠OAD=∠ODA.∵D为BE的下半圆弧的中点,∴OD⊥BE,∴∠ODA+∠OFD=90°.∴∠OAD+∠OFD=90°,∵∠OFD=∠AFC,∴∠OAD+∠AFC=90°.∵AC=FC,∴∠FAC=∠AFC,∴∠OAD+∠FAC=90°,即∠OAC=90°,∴OA⊥AC,∴AC是⊙O的切线.
(2)解:∵BF=8,OB=r,∴OF=8-r.∵在Rt△OFD中,OD2+OF2=DF2,∴r2+(8-r)2=()2,解得r=2(舍去)或r=6.
点拨:圆中和中点有关的问题常常结合垂径定理寻找解题方法.
(第3题)
4.证法一:连结DE,作DF⊥AC,垂足为F.
∵AB是⊙D的切线,∴DE⊥AB.
∵DF⊥AC,∴∠DEB=∠DFC=90°.
∵AB=AC,∴∠B=∠C.
又∵BD=CD,∴△BDE≌△CDF.
∴DF=DE.∴点F在⊙D上.
∴AC与⊙D相切.
证法二:连结DE,AD,作DF⊥AC,F是垂足.
∵AB与⊙D相切,∴DE⊥AB.
∵AB=AC,BD=CD,
∴∠DAB=∠DAC.
∵DE⊥AB,DF⊥AC,∴DE=DF.
∴点F在⊙D上.∴AC与⊙D相切.
专项训练三
1.解:连结OC,∵PC是⊙O的切线,
∴OC⊥PC,
∴△OPC为直角三角形.
∵PC=4,r=3,∴OP=5.易得OC2=OD·OP,即5·OD=9,
∴OD=.
2.解:连结OC,∵CD是⊙O的切线,
∴OC⊥CD.
∵AF⊥CD,∴AF∥OC.
∴∠A=∠BOC.
∵OC=OB,∴∠OCB=∠B.
∵AF=BF,∴∠A=∠B,
∴∠BOC=∠B=∠OCB.
∴∠B=60°,则∠A=60°.
3.证明:连结OD,∵CD是⊙O的切线,
∴OD⊥CD,
∴∠CDE+∠ODA=90°.∵CO⊥AB,
∴∠A+∠AEO=90°.
∵OA=OD,
∴∠A=∠ODA,
∴∠CDE=∠AEO=∠CED.
∴CD=CE.
4.证明:连结OE,
∵CE切⊙O于点E,∴OE⊥EC.
∵OB=BC,OB=OE,
∴在Rt△OEC中,OC=2OE,
∴∠C=30°,∴∠COE=60°.
∴∠A=∠COE=30°.
∵BD切⊙O于点B,∴AB⊥BD.
在Rt△ABD中,∠D=90°-∠A=60°.
在Rt△FBC中,∠BFC=90°-∠C=60°.∴∠DFE=∠BFC=60°.
∴∠D=∠DFE.
直线与圆的位置关系
专题训练
专项训练一:直线与圆的位置关系
名师点金:直线与圆的位置关系有相离、相切、相交三种情况,考查方向主要体现在:根据已知条件判断直线与圆的位置关系,根据直线与圆的位置关系求值或取值范围,有关直线与圆的位置关系的动态探究等.
根据d与r的大小关系判断直线与圆的位置关系
1.在平面直角坐标系中,以点(2,3)为圆心,2为半径的圆必定( )
A.与x轴相离,与y轴相切
B.与x轴、y轴都相离
C.与x轴相切,与y轴相离
D.与x轴、y轴都相切
2.已知⊙O的半径为2,圆心O到直线AB的距离为d,且方程x2-2x+d=0没有实数根,试确定直线AB与⊙O的位置关系.
根据直线与圆的位置关系求值或取值范围
3.如图,⊙P的半径为2,圆心P是抛物线y=x2-1上的点,当⊙P与x轴相切时,圆心P的坐标为________.
(第3题)
4.如图,直线l与⊙O相交于A,B两点,且与半径OC垂直,垂足为H,已知AB=16
cm,cos
∠OBH=.
(1)求⊙O的半径;
(2)如果要将直线l向下平移到与⊙O相离的位置,平移的距离应满足什么条件?
(第4题)
有关直线与圆的位置关系的动态探究
5.如图①,在四边形ABCD中,∠D=∠C=90°,AB=4,BC=6,AD=8.点P,Q同时从A点出发,分别做匀速运动,其中点P沿AB,BC向终点C运动,速度为每秒2个单位,点Q沿AD向终点D运动,速度为每秒1个单位.当这两点中有一点到达终点时,另一点也停止运动.设这两点运动了t秒.
(第5题)
(1)动点P与Q哪一点先到达终点?此时t为何值?(直接写出结果)
(2)当0<t<2时,求证:以PQ为直径的圆与AD相切(如图②).
(3)以PQ为直径的圆能否与CD相切?若能,求出t的值或取值范围;若不能,请说明理由.
专项训练二:证明切线的技巧
名师点金:有关切线的证明分两种情况:一是直线过圆上某一点,证明直线是圆的切线时,只需“连半径,
证垂直,得切线”;二是直线和圆没有已知的公共点时,
通常“作垂直,证半径,得切线”.
已知半径,证明垂直
1.如图,已知⊙O的半径OB=1,DE是⊙O的直径,过D作⊙O的切线,C是AD的中点,AE交⊙O于点B,四边形BCOE是平行四边形.
(1)求AD的长.
(2)BC是⊙O的切线吗?若是,请给出证明;若不是,请说明理由.
(第1题)
连半径,证垂直
类型1:连一条半径证垂直
2.如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论.
(第2题)
类型2:连两条半径证垂直
3.如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连结AD交BC于点F,若AC=FC.
(1)求证:AC是⊙O的切线;
(2)若BF=8,DF=,求⊙O的半径r.
(第3题)
作垂直,证半径
4.如图,AB=AC,D为BC的中点,⊙D与AB切于E点.求证:AC与⊙D相切.
(第4题)
专项训练三:切线性质的应用
名师点金:在应用切线的性质时,如果只有切线,没有半径,就要添加辅助线——连结过切点的半径,则此半径必垂直于切线.应用切线的性质能解决几何计算与证明中的有关问题.
利用切线的性质求线段的长度
1.如图,AB是⊙O的直径,P为AB延长线上的一点,PC切⊙O于C,CD⊥AB于D.若PC=4,⊙O的半径为3,求OD的长.
(第1题)
利用切线的性质求角的度数
2.如图,AB是⊙O的直径,CD切⊙O于C,AE⊥CD于E,BC的延长线与AE的延长线交于F,且AF=BF,求∠A的度数.
(第2题)
利用切线的性质证明线段相等
3.如图,AB是⊙O的直径,CO⊥AB,CD切⊙O于D,AD交CO于E.求证:CD=CE.
(第3题)
利用切线的性质证明角相等
4.如图,AB是⊙O的直径,BD切⊙O于点B,延长AB到C,使BC=OB,过点C作⊙O的切线,E为切点,与BD交于点F,AE的延长线交BD于点D.
求证:∠D=∠DFE.
(第4题)
答案
专项训练一
1.A
2.解:∵方程x2-2x+d=0没有实数根,
∴(-2)2-4d<0,
即d>1.
当1<d<2时,直线AB与⊙O相交;
当d=2时,直线AB与⊙O相切;
当d>2时,直线AB与⊙O相离.
3.(,2)或(-,2)
点拨:当⊙P与x轴相切时,由⊙P的半径为2,且圆的切线垂直于过切点的半径,可得P点纵坐标为2;又P在抛物线y=x2-1上,故将y=2代入得:2=x2-1,解得:x1=,x2=-.
4.解:(1)∵直线l与半径OC垂直,∴HB=AB=×16=8(cm).
∵cos
∠OBH==,∴OB=HB=×8=10(cm),即⊙O的半径为10
cm.
(2)在Rt△OBH中,OH===6(cm).
∴CH=OC-OH=10-6=4(cm).
∴将直线l向下平移到与⊙O相离的位置时,平移的距离必须大于4
cm.
5.(1)解:点P先到达终点,此时t=5.
(2)证明:如图,过点B作BM⊥AD,垂足为M,设圆与AB交于N,易得AM=2.
(第5题)
又∵AB=4,∴∠A=60°.
连结QN,∵PQ为直径,∴∠QNP=90°,∴∠NQA=30°.
∵AQ=t,AP=2t,∴AN=t,∴PN=t,NQ=t,∴PQ==t.
∴AQ2+PQ2=AP2.
∴△APQ为直角三角形,且∠AQP=90°.
∴以PQ为直径的圆与AD相切.
(3)解:能.设圆心为F,作FE⊥CD于E,PH⊥AD于H.∵CP=10-2t,DQ=8-t,∴EF=(CP+DQ)=(18-3t),PQ=2EF=18-3t.
∵PQ2=PH2+HQ2,且PH=AB·sin60°=2,
HQ=(8-t)-(10-2t)=t-2,
∴(t-2)2+(2)2=(18-3t)2.
解得t=或t=(舍去).
故当t=时,以PQ为直径的圆与CD相切.
专项训练二
1.解:(1)连结BD,∵DE是直径,∴∠DBE=∠ABD=90°.
∵四边形BCOE是平行四边形,
∴BC∥OE,BC=OE=1.
在Rt△ABD中,∵C为AD的中点,
∴BC=AD=1,∴AD=2.
(2)是,理由如下:
∵BC∥OD,BC=OD,∴四边形BCDO为平行四边形.
∵AD为⊙O的切线,∴OD⊥AD,
∴四边形BCDO为矩形.∴OB⊥BC.
∴BC是⊙O的切线.
2.(1)证明:连结CD.
∵BC是⊙O的直径,∴CD⊥AB.
又∵BC=AC,∴点D是AB的中点.
(2)解:DE与⊙O相切.证明如下:
连结OD,∵OD=OC,∴∠ODC=∠OCD.
又∵BC=AC,D是AB的中点,
∴∠BCD=∠ACD.
∵DE⊥AC,∴∠ACD+∠CDE=90°,
∴∠ODC+∠CDE=90°,
∴OD⊥DE.又∵OD为⊙O的半径,
∴DE是⊙O的切线.
3.(1)证明:如图,连结OA,OD,则OA=OD,∴∠OAD=∠ODA.∵D为BE的下半圆弧的中点,∴OD⊥BE,∴∠ODA+∠OFD=90°.∴∠OAD+∠OFD=90°,∵∠OFD=∠AFC,∴∠OAD+∠AFC=90°.∵AC=FC,∴∠FAC=∠AFC,∴∠OAD+∠FAC=90°,即∠OAC=90°,∴OA⊥AC,∴AC是⊙O的切线.
(2)解:∵BF=8,OB=r,∴OF=8-r.∵在Rt△OFD中,OD2+OF2=DF2,∴r2+(8-r)2=()2,解得r=2(舍去)或r=6.
点拨:圆中和中点有关的问题常常结合垂径定理寻找解题方法.
(第3题)
4.证法一:连结DE,作DF⊥AC,垂足为F.
∵AB是⊙D的切线,∴DE⊥AB.
∵DF⊥AC,∴∠DEB=∠DFC=90°.
∵AB=AC,∴∠B=∠C.
又∵BD=CD,∴△BDE≌△CDF.
∴DF=DE.∴点F在⊙D上.
∴AC与⊙D相切.
证法二:连结DE,AD,作DF⊥AC,F是垂足.
∵AB与⊙D相切,∴DE⊥AB.
∵AB=AC,BD=CD,
∴∠DAB=∠DAC.
∵DE⊥AB,DF⊥AC,∴DE=DF.
∴点F在⊙D上.∴AC与⊙D相切.
专项训练三
1.解:连结OC,∵PC是⊙O的切线,
∴OC⊥PC,
∴△OPC为直角三角形.
∵PC=4,r=3,∴OP=5.易得OC2=OD·OP,即5·OD=9,
∴OD=.
2.解:连结OC,∵CD是⊙O的切线,
∴OC⊥CD.
∵AF⊥CD,∴AF∥OC.
∴∠A=∠BOC.
∵OC=OB,∴∠OCB=∠B.
∵AF=BF,∴∠A=∠B,
∴∠BOC=∠B=∠OCB.
∴∠B=60°,则∠A=60°.
3.证明:连结OD,∵CD是⊙O的切线,
∴OD⊥CD,
∴∠CDE+∠ODA=90°.∵CO⊥AB,
∴∠A+∠AEO=90°.
∵OA=OD,
∴∠A=∠ODA,
∴∠CDE=∠AEO=∠CED.
∴CD=CE.
4.证明:连结OE,
∵CE切⊙O于点E,∴OE⊥EC.
∵OB=BC,OB=OE,
∴在Rt△OEC中,OC=2OE,
∴∠C=30°,∴∠COE=60°.
∴∠A=∠COE=30°.
∵BD切⊙O于点B,∴AB⊥BD.
在Rt△ABD中,∠D=90°-∠A=60°.
在Rt△FBC中,∠BFC=90°-∠C=60°.∴∠DFE=∠BFC=60°.
∴∠D=∠DFE.
