5.1矩形1 课件

课件20张PPT。5.1 矩形教学目标：
1. 经历矩形的概念、性质的发现过程.
2. 掌握矩形的概念.
3. 掌握矩形的性质定理“矩形的四个角都是直角”.
4. 掌握矩形的性质定理“矩形的对角线相等”.
5. 探索矩形的对称性.
重难点：
●本节教学的重点是矩形的性质.
●矩形的对称性的推理过程不容易理解，是本节教学的难点.
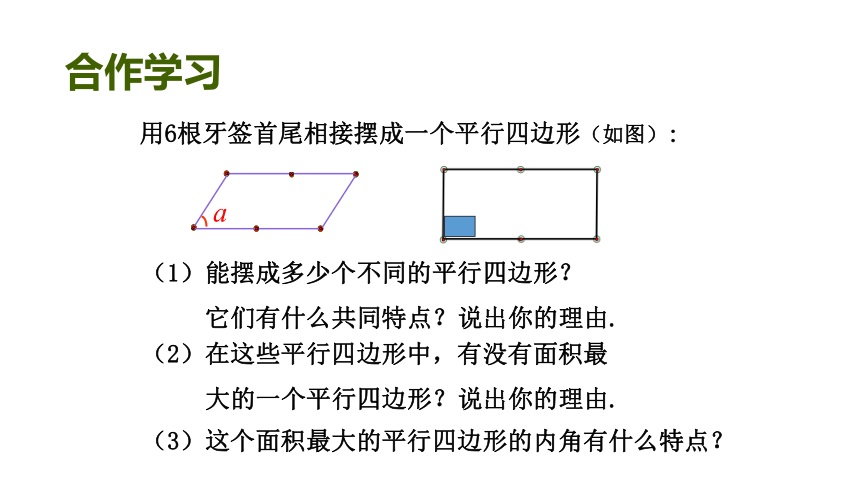
合作学习 用6根牙签首尾相接摆成一个平行四边形（如图）:（1）能摆成多少个不同的平行四边形？
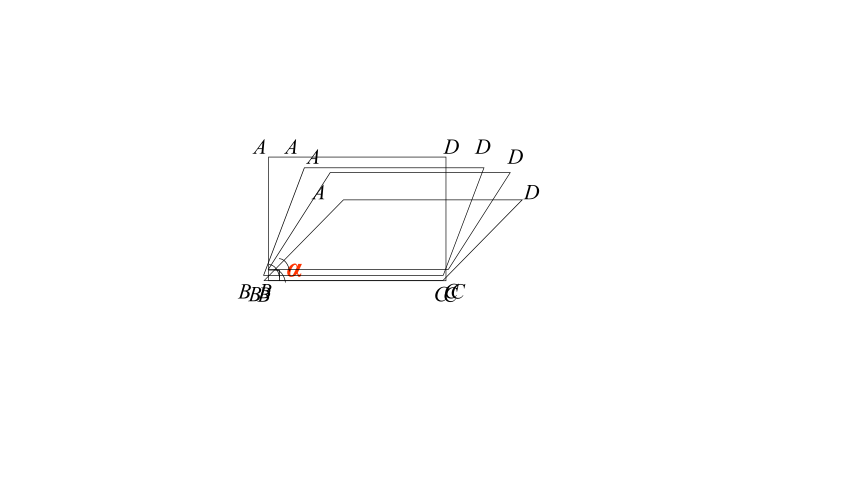
它们有什么共同特点？说出你的理由.（2）在这些平行四边形中，有没有面积最
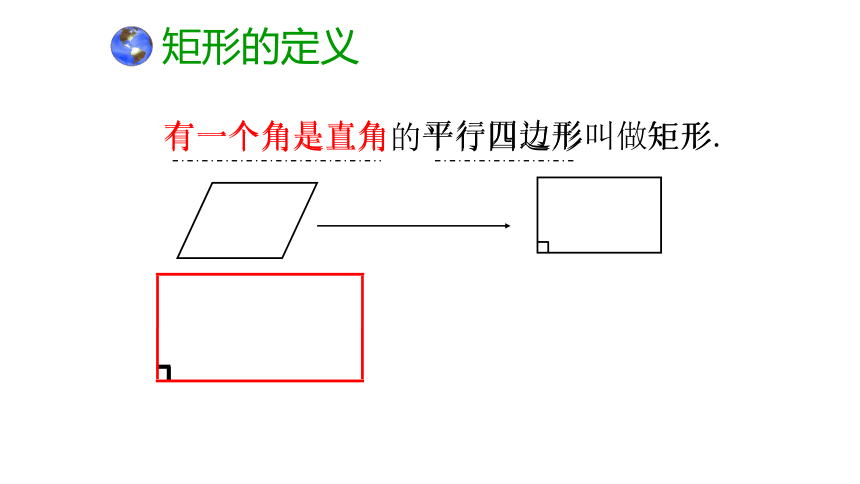
大的一个平行四边形？说出你的理由.（3）这个面积最大的平行四边形的内角有什么特点？a平行四边形 有一个角是直角的平行四边形叫做矩形.有一个角是直角矩形 平行四边形有哪些性质?从边、角、对角线、对称性,大家说说看.
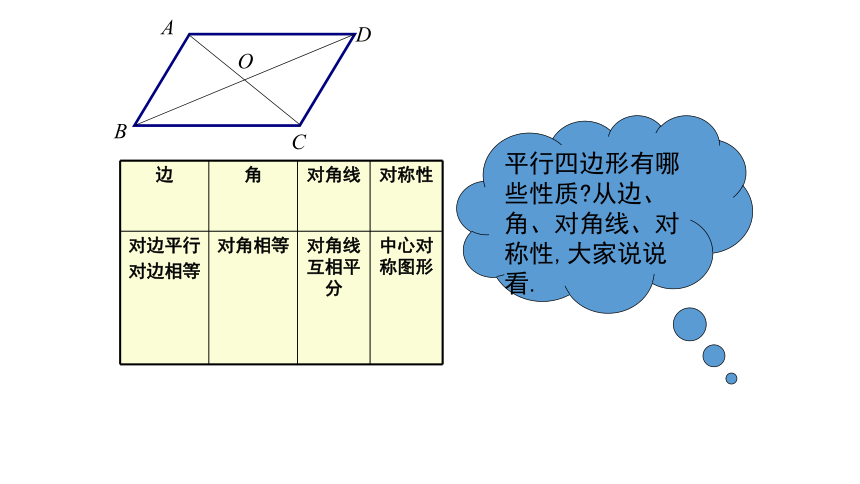
ABCD矩形是特殊的平行四边形，那它有什么特殊的性质吗？请你与你的同伴一起动手找一找.
O探索矩形性质已知：如图,四边形ABCD是矩形，
求证：∠ABC = ∠DCB = ∠BAC = ∠CDB = 90°.
1矩形的四个角都是直角性质证明：∵四边形ABCD是矩形，探索矩形性质已知：如图,四边形ABCD是矩形，
求证：AC = BD．∴∠ABC = ∠DCB = 90°，∴△ABC≌△DCB（SAS）. ∴AC = BD. 2矩形的对角线相等．性质在△ABC和△DCB中，AB = DC. AB = DC，
∠ABC = ∠DCB，
BC = CB，矩形既是中心对称图形，又是轴对称图形.
O矩形的特殊性矩形的对称中心到矩形四个顶点的距离相等例1: 已知:矩形ABCD的两条对角线AC、BD相交于点O, ∠AOD=120°, AB = 4cm,
求（1）判断△AOB的形状；
（2）矩形对角线的长.∴△AOB是等边三角形 （2）∵AB=4cm，
∴AC=BD=2AB=8cm，即矩形的对角线长8cm.解：（1）∵四边形ABCD是矩形， ∴AC=BD∴OA=OB∵∠AOD=120°∴∠AOB=60° ABCDO探索矩形的对称性:矩形是中心对称图形,又是轴对称图形矩形是轴对称图形吗？对称轴有几条?是中心对称图形吗？课内练习1.已知：如图，在矩形ABCD中，E,F分别是AB,CD的中点.求证：四边形AEFD是矩形.证明 在矩形ABCD中，
CD=AB，CD∥AB.∴DF=AE，DF∥AE.∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形).又∵∠A=Rt∠(矩形的四个角都是直角)，∴四边形AEFD是矩形.2.如图,矩形ABCD的两条对角线相交于点O.图中有多少对全等三角形?请把它们写出来.课内练习解 △AOD≌△BOC，
△AOB≌△DOC，
△ABD≌△BAC，
△ABD≌△CDB，△ABD≌△DCA，
△BAC≌△CDB，△BAC≌△DCA，△CDB≌△DCA，
共有八对.3.已知矩形的周长为56,对角线的交点到短边的距离比到长边的距离大4.求矩形的各边长.课内练习解 设矩形对角线的交点到短边的距离为x，
则对角线的交点到长边的距离为x-4，∴周长=4[x+(x-4)]=56.∴x=9.∴矩形的短边长为10，长边长为18.