浙教版八年级下6.3反比例函数的应用 同步练习(含答案)
文档属性
| 名称 | 浙教版八年级下6.3反比例函数的应用 同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 78.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-11 00:00:00 | ||
图片预览

文档简介
6.3反比例函数的应用
一、选择题
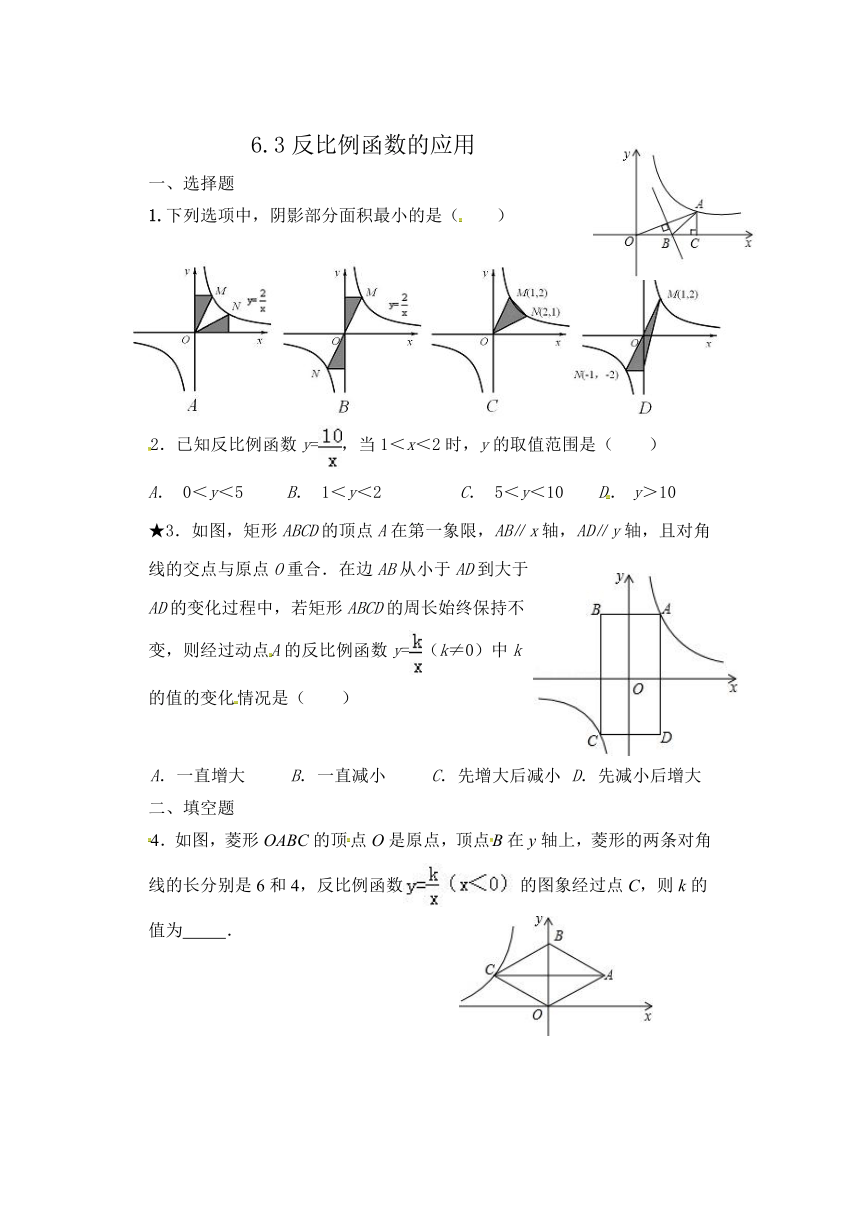
1.下列选项中,阴影部分面积最小的是(
)
2.已知反比例函数y=,当1<x<2时,y的取值范围是( )
A.
0<y<5
B.
1<y<2
C.
5<y<10
D.
y>10
★3.如图,矩形ABCD的顶点A在第一象限,AB∥x轴,AD∥y轴,且对角线的交点与原点O重合.在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数y=(k≠0)中k的值的变化情况是( )
A.
一直增大
B.
一直减小
C.
先增大后减小
D.
先减小后增大
二、填空题
4.如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数的图象经过点C,则k的值为
.
5.如图,点A(3,n)在双曲线y=上,过点A作
AC⊥x轴,垂足为C.线段OA的垂直平分线交OC于点B,则△ABC周长的值是
.
6.如图,在直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(3a,a)是反比例函数(k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为
.
三、解答题
7.如图,点A、B分别在x,y轴上,点D在第一象限内,DC⊥x轴于点C,AO=CD=2,AB=DA=,反比例函数y=(k>0)的图象过CD的中点E.
(1)求证:△AOB≌△DCA;
(2)求k的值;
(3)△BFG和△DCA关于某点成中心对称,其中点F在y轴上,是判断点G是否在反比例函数的图象上,并说明理由.
参考答案
1、C
2、C
3、C
4、-6
5、4
6、
7、(1)证明:∵点A、B分别在x,y轴上,点D在第一象限内,DC⊥x轴,∴∠AOB=∠DCA=90°,在Rt△AOB和Rt△DCA中,∴Rt△AOB≌Rt△DCA;(2)解:在Rt△ACD中,CD=2,AD=,∴AC==1,∴OC=OA+AC=2+1=3,∴D点坐标为(3,2),∵点E为CD的中点,∴点E的坐标为(3,1),k=3×1=3;(3)解:点G在反比例函数的图象上.理由如下:∵△BFG和△DCA关于某点成中心对称,∴△BFG≌△DCA,∴FG=CA=1,BF=DC=2,∠BFG=∠DCA=90°,而OB=AC=1,∴OF=OB+BF=1+2=3,∴G点坐标为(1,3),∵1×3=3,∴G(1,3)在反比例函数y=的图象上.
一、选择题
1.下列选项中,阴影部分面积最小的是(
)
2.已知反比例函数y=,当1<x<2时,y的取值范围是( )
A.
0<y<5
B.
1<y<2
C.
5<y<10
D.
y>10
★3.如图,矩形ABCD的顶点A在第一象限,AB∥x轴,AD∥y轴,且对角线的交点与原点O重合.在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数y=(k≠0)中k的值的变化情况是( )
A.
一直增大
B.
一直减小
C.
先增大后减小
D.
先减小后增大
二、填空题
4.如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数的图象经过点C,则k的值为
.
5.如图,点A(3,n)在双曲线y=上,过点A作
AC⊥x轴,垂足为C.线段OA的垂直平分线交OC于点B,则△ABC周长的值是
.
6.如图,在直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(3a,a)是反比例函数(k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为
.
三、解答题
7.如图,点A、B分别在x,y轴上,点D在第一象限内,DC⊥x轴于点C,AO=CD=2,AB=DA=,反比例函数y=(k>0)的图象过CD的中点E.
(1)求证:△AOB≌△DCA;
(2)求k的值;
(3)△BFG和△DCA关于某点成中心对称,其中点F在y轴上,是判断点G是否在反比例函数的图象上,并说明理由.
参考答案
1、C
2、C
3、C
4、-6
5、4
6、
7、(1)证明:∵点A、B分别在x,y轴上,点D在第一象限内,DC⊥x轴,∴∠AOB=∠DCA=90°,在Rt△AOB和Rt△DCA中,∴Rt△AOB≌Rt△DCA;(2)解:在Rt△ACD中,CD=2,AD=,∴AC==1,∴OC=OA+AC=2+1=3,∴D点坐标为(3,2),∵点E为CD的中点,∴点E的坐标为(3,1),k=3×1=3;(3)解:点G在反比例函数的图象上.理由如下:∵△BFG和△DCA关于某点成中心对称,∴△BFG≌△DCA,∴FG=CA=1,BF=DC=2,∠BFG=∠DCA=90°,而OB=AC=1,∴OF=OB+BF=1+2=3,∴G点坐标为(1,3),∵1×3=3,∴G(1,3)在反比例函数y=的图象上.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
