5.2菱形（第2课时）课件

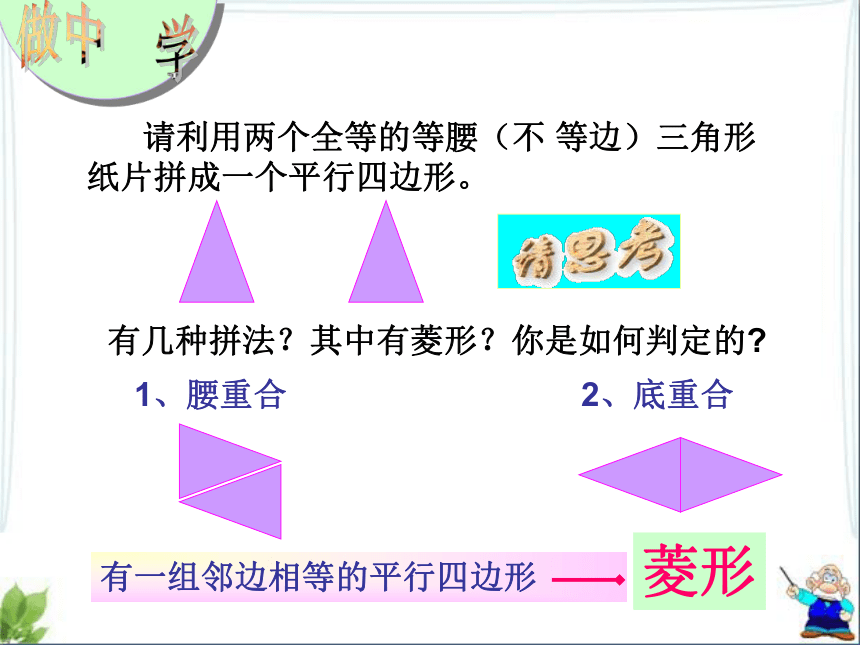
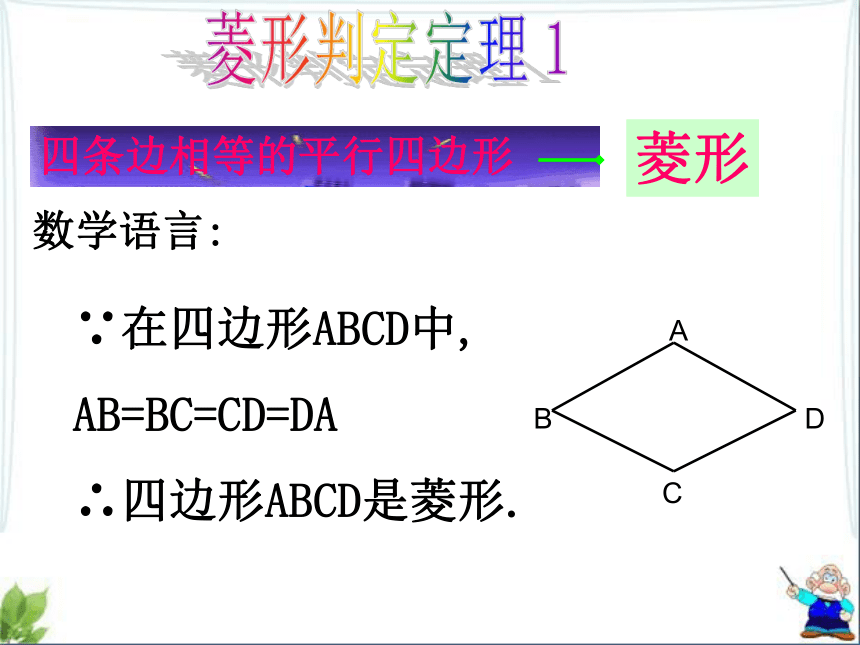
课件16张PPT。5.2菱形（第2课时）浙教版八年级下册第五章（1）菱形的定义是什么？ （2）菱形有哪些性质？回 顾一组邻边相等的平行四边形叫做菱形1.具有平行四边形的一切性质。2.菱形本身具有的特殊性质:四条边相等, 两条对角线互相垂直平分, 每一条对角线平分一组对角. 请利用两个全等的等腰（不 等边）三角形 纸片拼成一个平行四边形。 有几种拼法？其中有菱形？你是如何判定的?2、底重合1、腰重合菱形（1）判定一个四边形是不是菱形可根据什么？（2）菱形还有其他判定方法吗？定义法菱形数学语言:∵在四边形ABCD中,
AB=BC=CD=DA
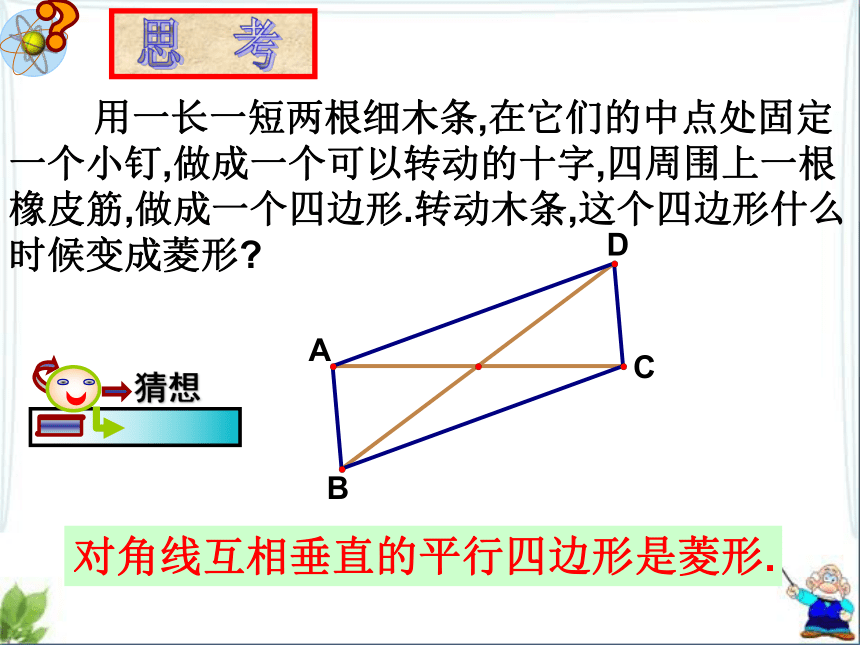
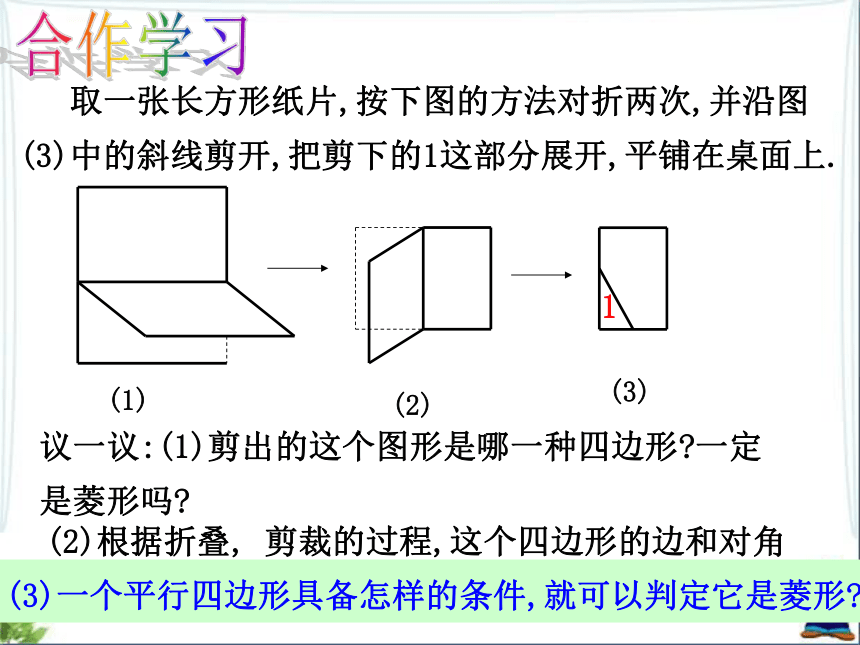
∴四边形ABCD是菱形.ABCD菱形判定定理１思　考 用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形?对角线互相垂直的平行四边形是菱形. 取一张长方形纸片,按下图的方法对折两次,并沿图(3)中的斜线剪开,把剪下的1这部分展开,平铺在桌面上.(1)(2)(3)1合作学习议一议:(1)剪出的这个图形是哪一种四边形?一定是菱形吗?(2)根据折叠, 剪裁的过程,这个四边形的边和对角线分别具有什么性质?(3)一个平行四边形具备怎样的条件,就可以判定它是菱形?菱形判定定理:定理1.四条边相等的四边形是菱形.定理2.对角线互相垂直的平行四边形是菱形.已知:在平行四边形ABCD中,BD⊥AC,O为垂足.
求证:平行四边形ABCD是菱形.证明：∵四边形ABCD是平行四边形
∴AO=OC
∵BD⊥AC
∴AD=CD∴平行四边形ABCD是菱形菱形的判定：四条边都相等的四边形是菱形.∵AB=BC=CD=DA∴四边形ABCD是菱形对角线互相垂直的平行四边形是菱形∵□ABCD，AC⊥BD∴ □ABCD是菱形一组邻边相等对角线互相垂直四条边相等四种判定方法四边形菱形的判定方法：1、画一个菱形，使它的两条对角线的长分别为4cm和6cm。o6cm4cm练一练（1）两条对角线互相垂直的四边形是菱形. ( )2、辨一辨（2）两条对角线互相垂直平分的四边形是菱形. ( )错对判断下列说法是否正确？为什么？
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形；
(4)两条邻边相等，且一条对角线平分一
组对角的四边形是菱形． □ABCD的对角线AC与BD相交于点O，
（1）若AB=AD，则□ABCD是 形； （2）若AC=BD，则□ABCD是 形； （3）若∠ABC是直角，则□ABCD是 形； （4）若∠BAO=∠DAO，则□ABCD是 形。矩菱矩菱 ADCB 例2、如图，在 矩形ABCD中，对角线AC垂直平分与AD，BC分别交于E，F.求证：四边形AFCE是菱形OEF证明:∵四边形ABCD是矩形,
∴AE//FC(矩形的定义)
∴∠EAC=∠ACF
又∵∠AOE=∠COF,AO=CO,
∴△AOE≌△COF,
∴EO=FO.
∴四边形是平行四边形
(对角线相互平分的四边形是平行四边形).
∵EF⊥AC
∴四边形AFCE是菱形
(对角线互相垂直的平行四边形是菱形). （2）∵ 四边形ABCD是平行四边形，
∵AC⊥BD
∴四边形ABCD是菱形.（2）四边形ABCD是菱形吗？为什么？练一练:全课小结——菱形的判定∵AB=BC=CD=DA∴四边形ABCD是菱形∵□ABCDAC⊥BD∴四边形ABCD是菱形∵□ABCDAB=AD∴四边形ABCD是菱形四边相等的四边形是菱形对角线互相垂直的平行四边形是菱形一组邻边相等的平行四边形是菱形