5.3正方形（2）课件

(共17张PPT)
5.3正方形（2）
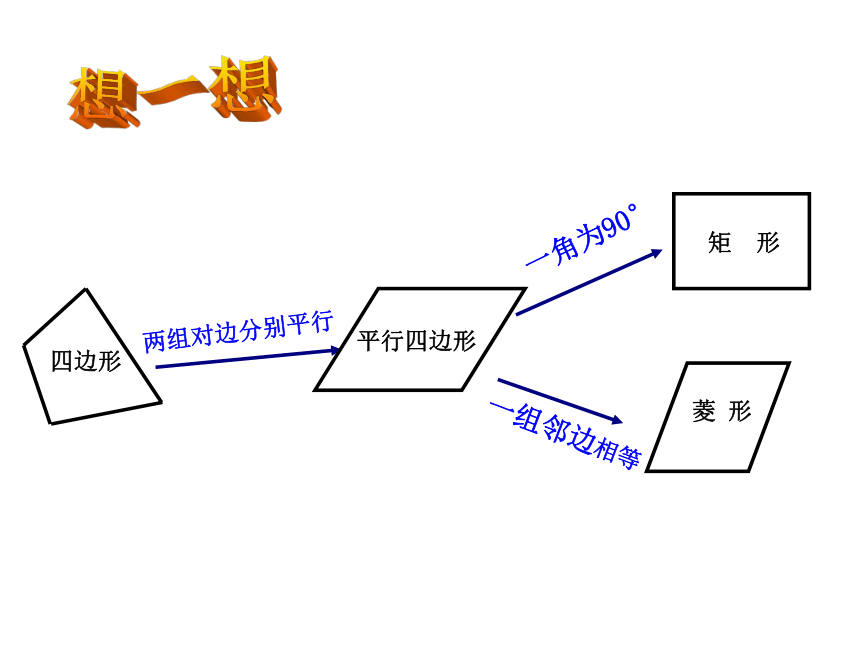
四边形
两组对边分别平行
平行四边形
矩 形
菱 形
一角为90°
一组邻边相等
矩 形
正方形
〃
〃
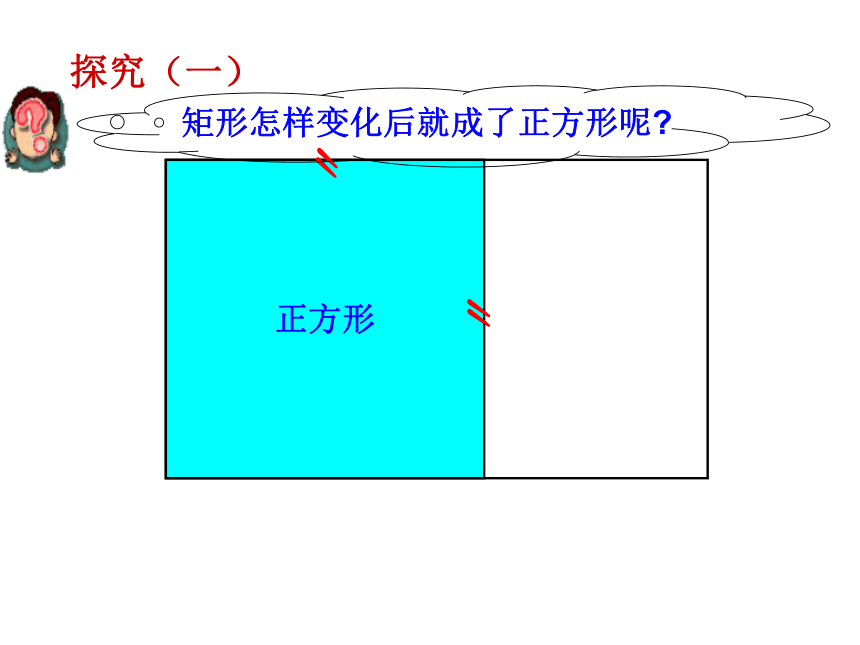
矩形怎样变化后就成了正方形呢
探究（一）
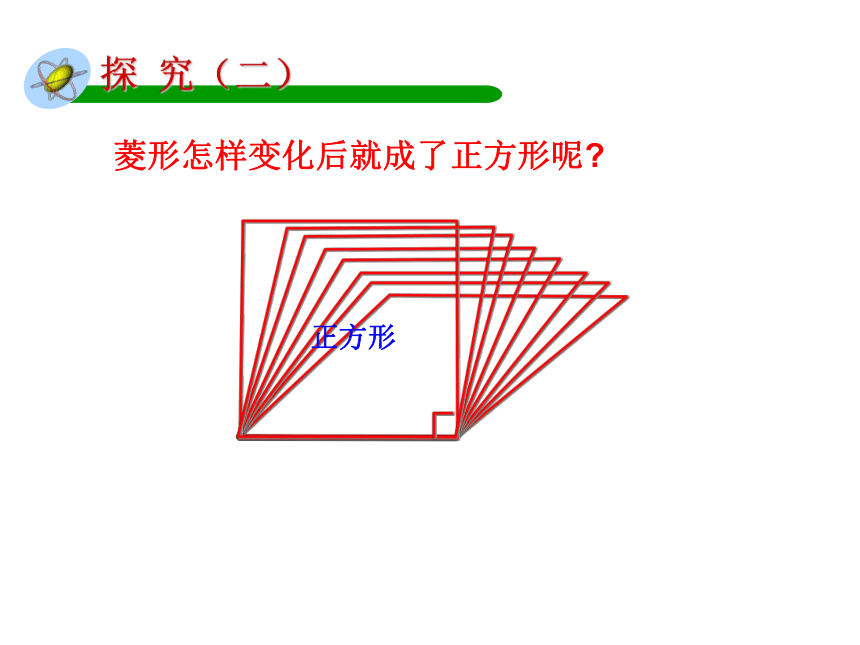
探 究（二）
菱形怎样变化后就成了正方形呢
正方形
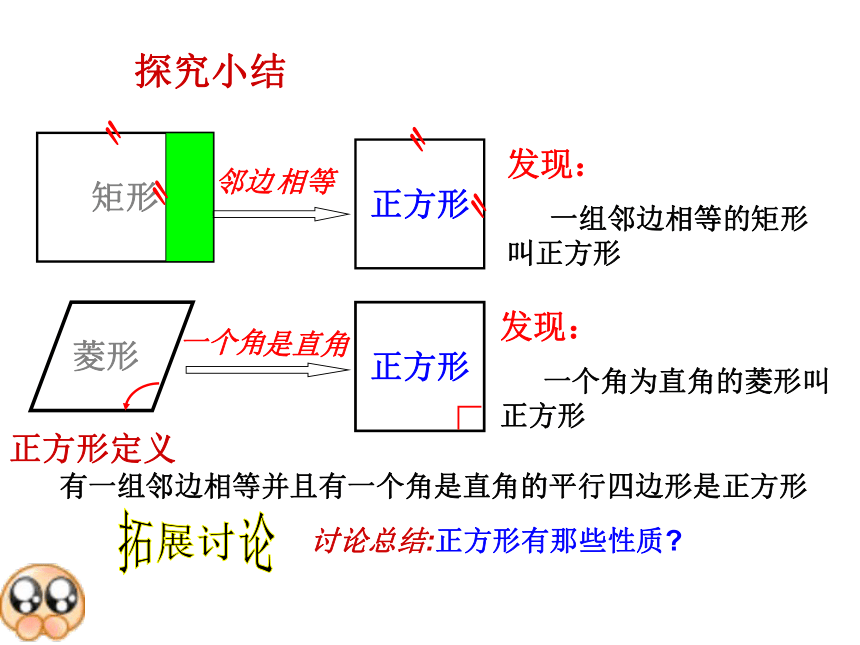
探究小结
矩形
〃
〃
正方形
邻边
相等
〃
〃
发现：
一组邻边相等的矩形 叫正方形
菱形
一个角
是直角
正方形
∟
发现：
一个角为直角的菱形叫正方形
正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
讨论总结:正方形有那些性质
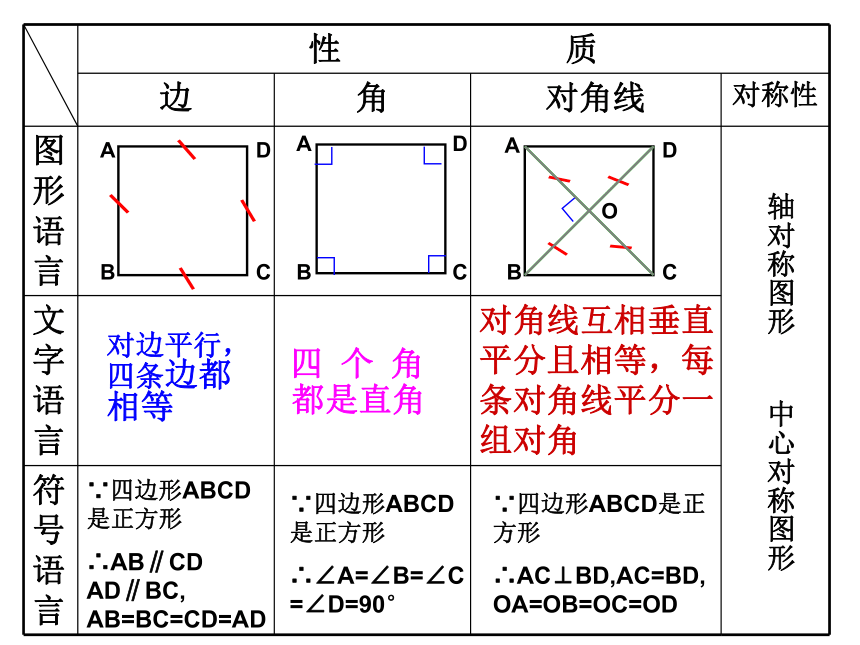
性 质
边 角 对角线 对称性
图形语言
文字语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
对边平行， 四条边都相等
四 个 角
都是直角
对角线互相垂直平分且相等，每条对角线平分一组对角
∵四边形ABCD是正方形
∴AB∥CD AD∥BC, AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD
轴对称图形 中心对称图形
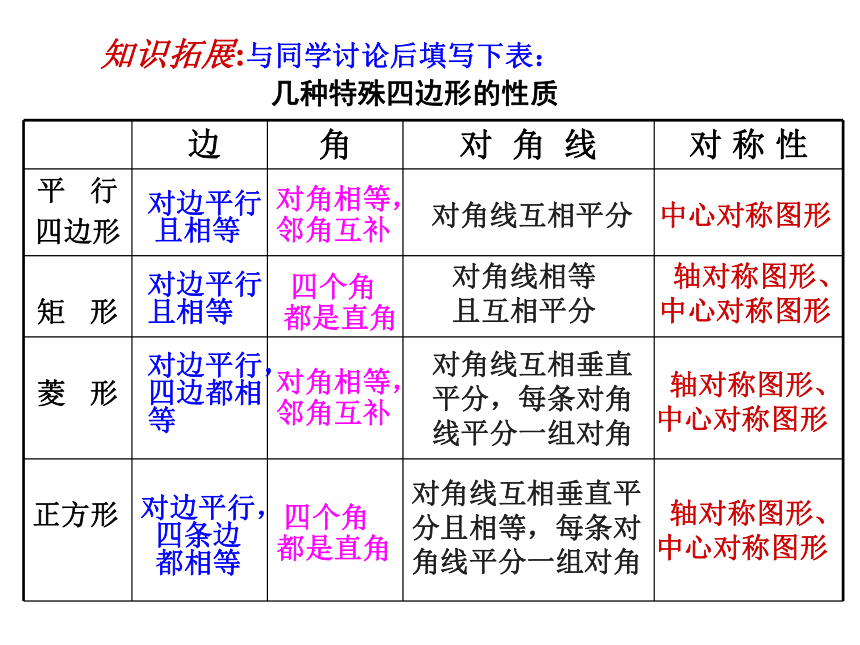
知识拓展:与同学讨论后填写下表：
边 角 对 角 线 对 称 性
平 行
四边形
矩 形
菱 形
正方形
几种特殊四边形的性质
对边平行
且相等
对边平行 且相等
对边平行，四边都相等
对边平行，
四条边
都相等
对角相等，
邻角互补
四个角
都是直角
对角相等，
邻角互补
四个角
都是直角
对角线互相平分
对角线相等
且互相平分
对角线互相垂直平分，每条对角线平分一组对角
对角线互相垂直平分且相等，每条对角线平分一组对角
中心对称图形
轴对称图形、
中心对称图形
轴对称图形、
中心对称图形
轴对称图形、
中心对称图形
平行四边形
矩形
菱形
正
方
形
正方形、菱形、矩形、平行四边形四者之间有什么关系？
例
求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
这是一道文字证明题,该怎么做 你会做吗
第一步:根据题意画出图形
第二步:写出已知、求证
第三步：进行证明
A
D
C
B
O
已知:如图,四边形ABCD是正方形,对 角线AC、BD相交于点O.
求证:△ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO
分析:利用正方形的性质,对角线互相垂直平分且相等,每条对角线平分一组对角.平分可以产生线段等量关系,垂直可以产生直角,于是可以得到四个全等的等腰直角三角形.
A
D
C
B
O
正方形对角线把正方形分成多少个等腰直角三角形？
拓展讨论:
结论：
分成八个等腰直角三角形，分别是△ABC、 △ADC、 △ABD、 △BCD ；
△AOB、 △BOC、 △COD、 △DOA.
1.如图，在正方形ABCD中，E在BC的延长线上，且CE=AC，AE交CD于F，则求∠AFC的度数。
A
B
D
C
F
E
2．
已知：正方形ABCD对角线AC、BD相　　　　　　　交于点O，且AB＝2cm，如图(2)。
　求：AC的长及正方形的面积S。　　　　　　　　　　　
3．
已知：在正方形ABCD中，对角线AC、
　BD相交于点O，且AC＝6 cm，如图
求：正方形的面积S。　　　　　　　　　　　
4．如图(3)，正方形ABCD中，AC、BD相交于O，
分析：要证明BM＝CN，大家观察
图形可以考虑证哪两个三角形全等
MN∥AB且MN分别交OA、OB于M、N，
求证：BM＝CN。　　　　　　　　　
你能完成证明吗
　AB＝BC，∠1＝∠2＝45 °　　条件够吗？
　　还需要的条件是 AM＝BN
△ABM≌△BCN
你所要证明的两个三角形已经满足
了哪些条件
由正方形可以得到的条件有：
5．已知：如图(4)在正方形ABCD中，F为CD延长线
上一点，CE⊥AF于E，交AD于M，
　　 求证：∠MFD＝45°
分析：
欲证∠MFD＝45°，由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____
要证MD＝FD，大家只须证得哪两个三角形全等
试一试
看能不能完成证明
△CMD≌△ADF
谈谈本节课的收获
小结
1、正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
2、正方形有那些性质
对边平行，四条边都相等
四个角都是直角
对角线互相垂直平分且相等，
每条对角线平分一组对角
边：
角：
对角线：