浙教版八年级数学下4.2平行四边形及其性质(第1课时) 课件
文档属性
| 名称 | 浙教版八年级数学下4.2平行四边形及其性质(第1课时) 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-13 20:01:20 | ||
图片预览


文档简介
课件17张PPT。 4.2平行四边形及其性质
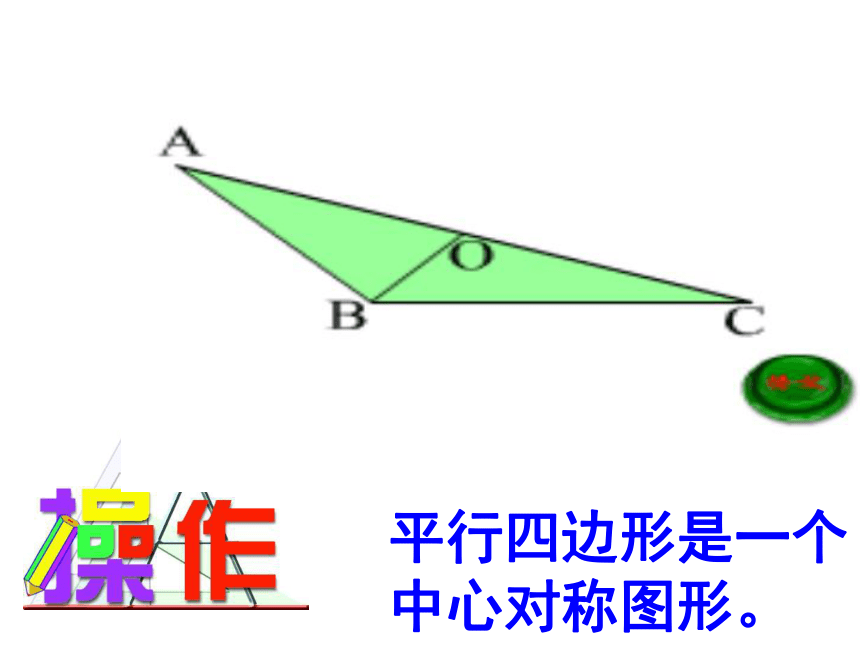
(第1课时)浙教版八年级下册第四章平行四边形是一个中心对称图形。两组对边分别平行四边形平行
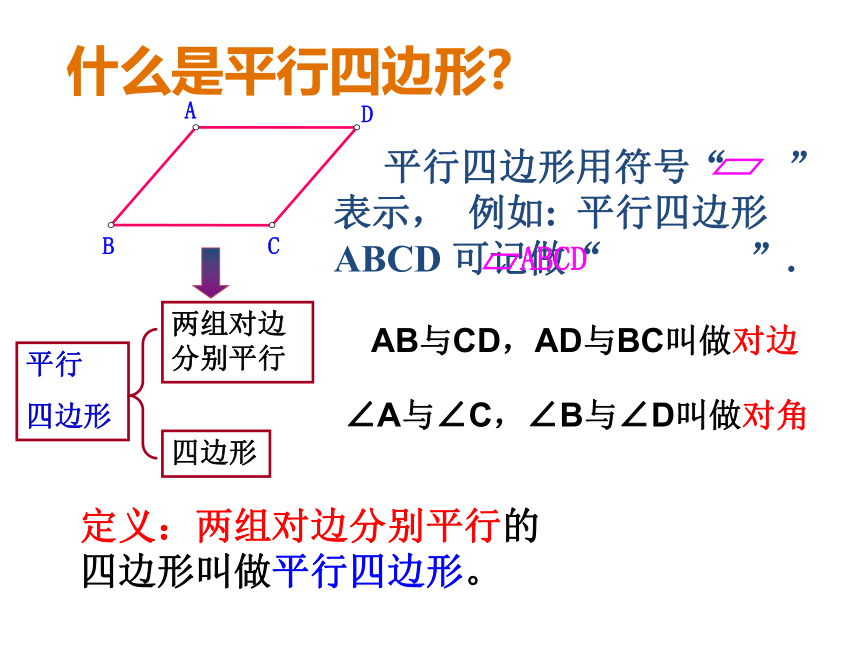
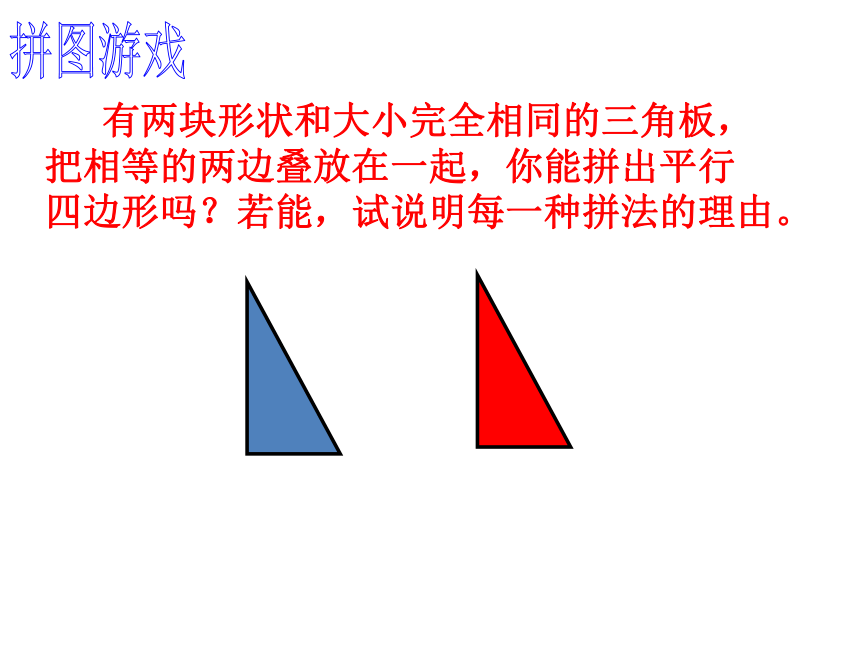
四边形 平行四边形用符号“ ”表示, 例如: 平行四边形ABCD 可记做“ ”.∠A与∠C,∠B与∠D叫做对角AB与CD,AD与BC叫做对边定义:两组对边分别平行的四边形叫做平行四边形。什么是平行四边形? 有两块形状和大小完全相同的三角板,把相等的两边叠放在一起,你能拼出平行
四边形吗?若能,试说明每一种拼法的理由。
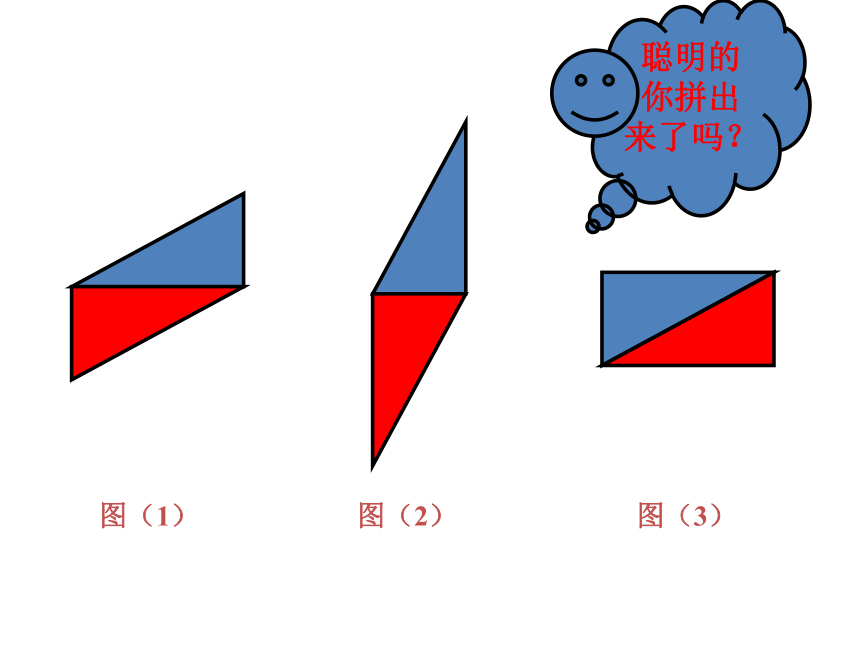
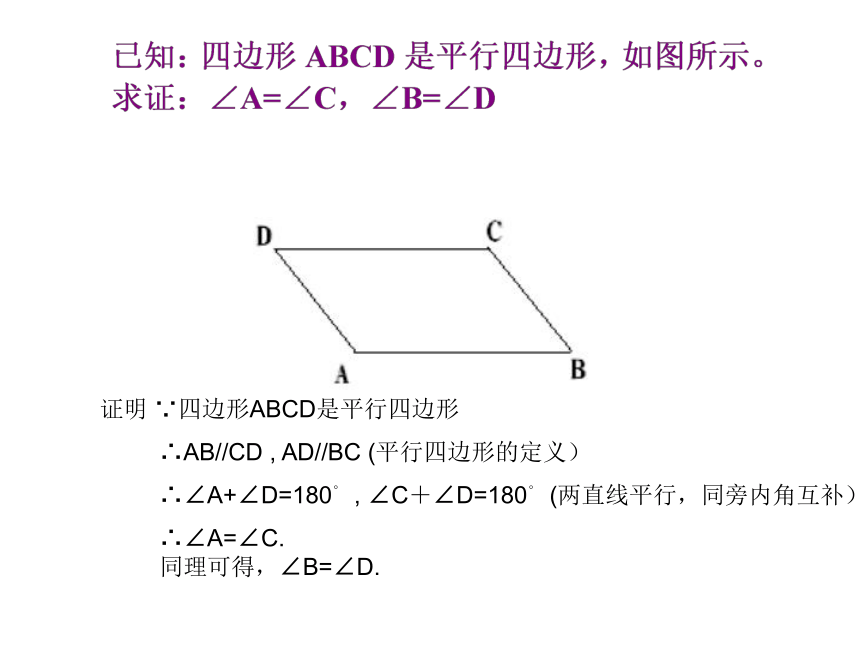
拼图游戏图(1)图(2)图(3) 证明 ∵四边形ABCD是平行四边形
∴AB//CD , AD//BC (平行四边形的定义)
∴∠A+∠D=180。 , ∠C+∠D=180。 (两直线平行,同旁内角互补)
∴∠A=∠C.
同理可得,∠B=∠D.
由此可以得到定理:
平行四边形的对角相等. 巩固练习一巩固练习二1、如图:在 中,AE⊥DC于E,AF⊥BC于F,∠EAF=65。,求 各个内角的度数。ABCDABCD平行四边形的性质已知:如图,四边形ABCD是平行四边形.求证:AB=CD,BC=DA.分析:要证明AB=CD,BC=DA可转化全等三角形的对应边来证明,于是可作辅助线来达到目的.证明:连接AC.∵四边形ABCD是平行四边形,∴AB∥CD,BC∥DA.∴∠1=∠2, ∠3=∠4.∵AC=CA,∴△ABC≌△CDA(ASA).∴AB=CD,BC=DA.由此可以得到定理:
平行四边形的对边相等.FE例1 已知:如图,E、F分别是平行四边形ABCD的边AD、BC上的点,且AF//CE。求证:DE=BF,
∠BAF= ∠DCE 。平行四边形的不稳定性在日常生活和生产中也有许多应用本节课
你有什么收获?课堂小结1、平行四边形的定义:两组对边分别平行的四边形。
2、平行四边形的对角相等。
3、平行四边形的对边相等。
(第1课时)浙教版八年级下册第四章平行四边形是一个中心对称图形。两组对边分别平行四边形平行
四边形 平行四边形用符号“ ”表示, 例如: 平行四边形ABCD 可记做“ ”.∠A与∠C,∠B与∠D叫做对角AB与CD,AD与BC叫做对边定义:两组对边分别平行的四边形叫做平行四边形。什么是平行四边形? 有两块形状和大小完全相同的三角板,把相等的两边叠放在一起,你能拼出平行
四边形吗?若能,试说明每一种拼法的理由。
拼图游戏图(1)图(2)图(3) 证明 ∵四边形ABCD是平行四边形
∴AB//CD , AD//BC (平行四边形的定义)
∴∠A+∠D=180。 , ∠C+∠D=180。 (两直线平行,同旁内角互补)
∴∠A=∠C.
同理可得,∠B=∠D.
由此可以得到定理:
平行四边形的对角相等. 巩固练习一巩固练习二1、如图:在 中,AE⊥DC于E,AF⊥BC于F,∠EAF=65。,求 各个内角的度数。ABCDABCD平行四边形的性质已知:如图,四边形ABCD是平行四边形.求证:AB=CD,BC=DA.分析:要证明AB=CD,BC=DA可转化全等三角形的对应边来证明,于是可作辅助线来达到目的.证明:连接AC.∵四边形ABCD是平行四边形,∴AB∥CD,BC∥DA.∴∠1=∠2, ∠3=∠4.∵AC=CA,∴△ABC≌△CDA(ASA).∴AB=CD,BC=DA.由此可以得到定理:
平行四边形的对边相等.FE例1 已知:如图,E、F分别是平行四边形ABCD的边AD、BC上的点,且AF//CE。求证:DE=BF,
∠BAF= ∠DCE 。平行四边形的不稳定性在日常生活和生产中也有许多应用本节课
你有什么收获?课堂小结1、平行四边形的定义:两组对边分别平行的四边形。
2、平行四边形的对角相等。
3、平行四边形的对边相等。
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
