浙教版八年级数学下6.3《反比例函数的应用》课件（共21张PPT）.zip

文档属性

名称	浙教版八年级数学下6.3《反比例函数的应用》课件（共21张PPT）
格式	zip
文件大小	935.2KB
资源类型	教案
版本资源	浙教版
科目	数学
更新时间	2017-03-15 00:00:00

点击下载

图片预览

1

2

3

4

5

6

7

8

9

文档简介

课件21张PPT。回顾：反比例函数的图象性质特征：图象是双曲线当k>0时,双曲线分别位于第一,三象限内
当k<0时, 双曲线分别位于第二,四象限内当k>0时,在每一象限内,y随x的增大而减小
当k<0时,在每一象限内,y随x的增大而增大双曲线无限接近于x、y轴,但永远不会与坐标轴相交双曲线既是轴对称图形又是中心对称图形.任意一组变量的乘积是一个定值,即xy=k形状位置增减性变化趋势对称性面积不变性
长方形面积︳m n︱＝︳K︱【例1】设?ABC中BC边的长为x（cm），BC上的高AD为y（cm）。 ?ABC的面积是常数。已知y关于x的函数图象过点（3，4）. (1) 求y关于x的函数解析式和?ABC 的面积？解:【例1】设?ABC中BC边的长为x（cm），BC上的高AD为y（cm）。已知y关于x的函数图象过点（3，4） (2)画出函数的图象。并利用图象，
求当2 < y < 6如果例1中BC=6cm。你能作出?ABC吗？
能作出多少个？请试一试。
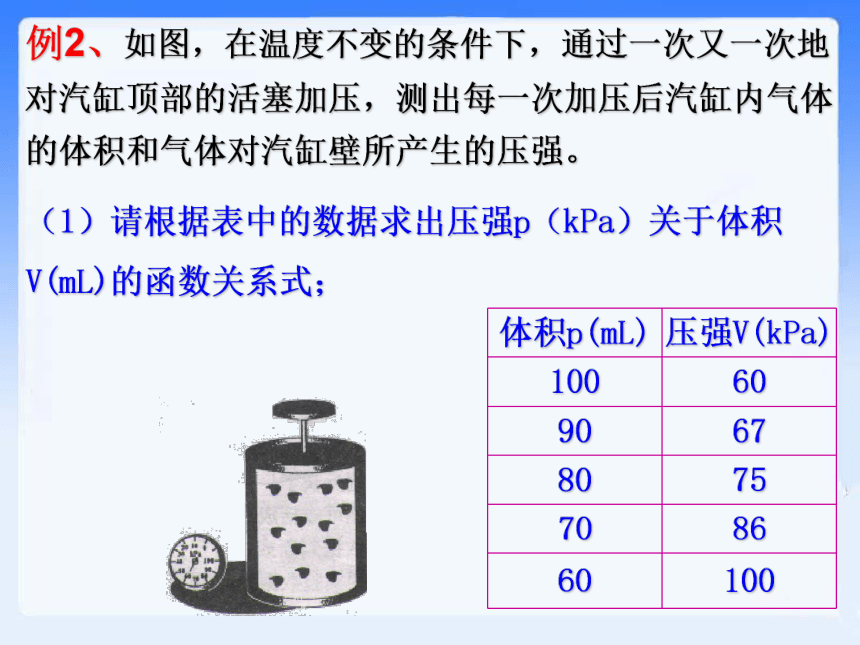
如果要求?ABC是等腰三角形呢？1、生产某种工艺品，设每名工人一天大约能做x个。若每天要生产这种工艺品60个，则需工人y名。（1）求y关于x的函数解析式；（2）若一名工人每天能做的工艺品个数最少6个，最多8个。估计每天需要做这种工艺品的工人多少人？练一练（1）请根据表中的数据求出压强p（kPa）关于体积V(mL)的函数关系式；例2、如图，在温度不变的条件下，通过一次又一次地对汽缸顶部的活塞加压，测出每一次加压后汽缸内气体的体积和气体对汽缸壁所产生的压强。⑴请根据表中的数据求出压强p（kPa）
关于体积V（ml）的函数关系式；例2、如图，在温度不变的条件下，通过一次又一次地对汽缸顶部的活塞加压，测出每一次加压后汽缸内气体的体积和气体对汽缸壁所产生的压强。解（1）根据函数图象，可选择反比例函数进行尝试，设解析式为p=k/V（k≠0），把点（60，100）代入，得：将点（70，86），（80，75），（90，67），（100，60）分别代入验证，均符合⑵当压力表读出的压强为72kPa时，汽缸内气体的体积压缩到多少ml？答:当压力表读出的压强为72kPa时，汽缸内气体的体积压缩到约83ml。例2、如图，在温度不变的条件下，通过一次又一次地对汽缸顶部的活塞加压，测出每一次加压后汽缸内气体的体积和气体对汽缸壁所产生的压强。本例反映了一种数学建模的方式，具体过程可概括成：
由实验获得数据——用描点法画出图象——根据图象和数据判断或估计函数的类别——用待定系数法求出函数关系式——用实验数据验证．例2中，若压强80⑵在应用反比例函数解决问题时,一定要注意以下几点:
①要注意自变量取值范围符合实际意义
②确定反比例函数之前一定要考察两个变量与定值之间的关系
若k未知时应首先由已知条件求出k值
③求“至少,最多”时可根据函数性质得到课堂小结补充练习D（1）一次函数的解析式；（2）求△AOB的面积； 2、已知一次函数的图象与反比例函数的图象交于A、B两点，且点A的横坐标和点B的纵坐标都是 -2。
3、有一个Rt△ABC,∠A=900,∠B=600,AB=1,将它放在直角坐标系中,使斜边BC在x轴上，直角顶点A在反比例函数的图象上,且点A在第一象限.求:点C的坐标． 3、（1）2A3、（2）o3、（3）C63、（4）