第2章一元二次方程单元试卷(A)含答案
文档属性
| 名称 | 第2章一元二次方程单元试卷(A)含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 159.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-17 16:02:49 | ||
图片预览


文档简介
浙教八年级(下)数学单元测试A卷
第2单元 一元二次方程
满分100分
时间100分钟
班级
姓名
一、选择题(每小题3分,共30分)
1.(2016秋 吴中区期末)一元二次方程:x2﹣9=0的解是( )
A.3
B.﹣3
C.±3
D.9
2.(2016 新都区模拟)下列方程中,关于x的一元二次方程是( )
A.(x+1)2=2(x+1)
B.
C.ax2+bx+c=0
D.x2+2x=x2﹣1
3.(2016 武汉校级模拟)将一元二次方程4x2+7=3x化成一般式后,二次项系数和一次项系数分别为( )
A.4,3
B.4,7
C.4,﹣3
D.4x2,﹣3x
4.(2016 新疆)一元二次方程x2﹣6x﹣5=0配方可变形为( )
A.(x﹣3)2=14
B.(x﹣3)2=4
C.(x+3)2=14
D.(x+3)2=4
5.(2016秋 简阳市期末)根据下列表格的对应值:
0.59
0.60
0.61
0.62
0.63
x2+x﹣1
﹣0.0619
﹣0.04
﹣0.0179
0.0044
0.0269
判断方程x2+x﹣1=0一个解的取值范围是( )
A.0.59<x<0.61
B.0.60<x<0.61
C.0.61<x<0.62
D.0.62<x<0.63
6.(2016 攀枝花)若x=﹣2是关于x的一元二次方程x2+ax﹣a2=0的一个根,则a的值为( )
A.﹣1或4
B.﹣1或﹣4
C.1或﹣4
D.1或4
7.(2016 桂林)若关于x的一元二次方程(k﹣1)x2+4x+1=0有两个不相等的实数根,则k的取值范围是( )
A.k<5
B.k<5,且k≠1
C.k≤5,且k≠1
D.k>5
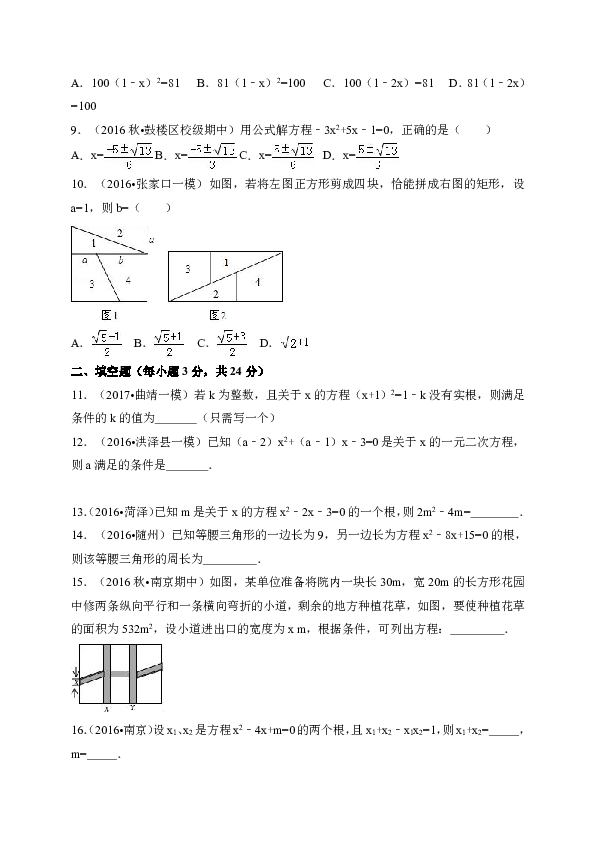
8.(2017 曲靖一模)为解决群众看病贵的问题,有关部门决定降低药价,对某种原价为100元的药品进行连续两次降价后为81元.设平均每次降价的百分率为x,则下列方程正确的是( )
A.100(1﹣x)2=81
B.81(1﹣x)2=100
C.100(1﹣2x)=81
D.81(1﹣2x)=100
9.(2016秋 鼓楼区校级期中)用公式解方程﹣3x2+5x﹣1=0,正确的是( )
A.x=
B.x=
C.x=
D.x=
10.(2016 张家口一模)如图,若将左图正方形剪成四块,恰能拼成右图的矩形,设a=1,则b=( )
A.
B.
C.
D.
二、填空题(每小题3分,共24分)
11.(2017 曲靖一模)若k为整数,且关于x的方程(x+1)2=1﹣k没有实根,则满足条件的k的值为
(只需写一个)
12.(2016 洪泽县一模)已知(a﹣2)x2+(a﹣1)x﹣3=0是关于x的一元二次方程,则a满足的条件是
.
13.(2016 菏泽)已知m是关于x的方程x2﹣2x﹣3=0的一个根,则2m2﹣4m=
.
14.(2016 随州)已知等腰三角形的一边长为9,另一边长为方程x2﹣8x+15=0的根,则该等腰三角形的周长为
.
15.(2016秋 南京期中)如图,某单位准备将院内一块长30m,宽20m的长方形花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图,要使种植花草的面积为532m2,设小道进出口的宽度为x
m,根据条件,可列出方程:
.
16.(2016 南京)设x1、x2是方程x2﹣4x+m=0的两个根,且x1+x2﹣x1x2=1,则x1+x2=
,m=
.
17.(2016秋 黄陂区期中)小明设计了一个魔术盒,当任意实数对(a,b)进入其中,会得到一个新的实数a2﹣2b+3.若将实数(x,﹣2x)放入其中,得到﹣1,则x=
.
18.(2016 句容市一模)将关于x的一元二次方程x2+bx+c=0变形为x2=﹣bx﹣c,就可得x2表示为关于x的一次多项式,从而达到“降次”的目的,我们称这样的方法为“降次法”.已知x2﹣x﹣1=0,可用“降次法”求得x4﹣3x+2016的值是
.
三.解答题(共46分)
19.(2016秋 仁寿县期中)用适当的方法解下列方程(12分)
(1)(x﹣2)2﹣9=0
(2)x2﹣2x﹣199=0.
(3)3x(x﹣1)=2x﹣2
(4)x2+3x+2=0.
20.(2016 新都区模拟)某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?(6分)
21.(2016秋 宁德期末)小明同学解一元二次方程x2﹣4x﹣1=0的过程如图所示(6分)
解:x2﹣4x=1…①
x2﹣4x+4=1
…②
(x﹣2)2=1…③
x﹣2=±1…④
x1=3,x2=1…⑤
(1)小明解方程的方法是
,他的求解过程从第
步开始出现错误,这一步的运算依据应该是
;
(2)解这个方程.
22.(2016 郑州模拟)已知关于x的方程x2﹣2(m+1)x+m2=0.(6分)
(1)当m取什么值时,原方程没有实数根;
(2)对m选取一个合适的非零整数,使原方程有两个不相等的实数根,并求出这两个实数根.
23.(2017 郑州一模)巩义长寿山景区门票价格为50元,在今年红叶节期问,为吸引游客,推出了如下优惠活动:如果人数不超过25人,门票按原价销售,如果人数超过25人,每超过1人,所购买的门票均降低1元,但人均门票不低于35元,某单位组织员工去长寿山看红叶,共支付门票费用1350元,请问该单位这次共有多少名员工去长寿山看红叶?(8分)
24.(2016 虞城县三模)你知道古代数学家怎样解一元二次方程吗?以x2﹣2x﹣3=0为例,大致过程如下:(8分)
第一步:将原方程变形为x2﹣2x=3,即x(x﹣2)=3.
第二步:构造一个长为x,宽为(x﹣2)的长方形,长比宽大2,且面积为3,如图1所示.
第三步:用四个这样的长方形围成一个大正方形,中间是一个小正方形,如图2所示.
第四步:计算大正方形面积用x表示为
.
由观察可得,大正方形面积等于四个长方形与小正方形面积之和,得方程
,两边开方可求得:x1=3,x2=﹣1.
(1)第四步中横线上应填入
;
.
(2)请参考古人的思考过程,解方程x2﹣x﹣1=0.
参考答案
一、选择题(每小题3分,共30分)
1.解:∵x2=9,
∴x=3或x=﹣3,
故选:C.
2.解:下列方程中,关于x的一元二次方程是(x+1)2=2(x+1),
故选A.
3.解:4x2+7=3x,
4x2﹣3x+7=0,
二次项系数和一次项系数分别为4、﹣3,
故选C.
4.解:x2﹣6x﹣5=0,
x2﹣6x=5,
x2﹣6x+9=5+9,
(x﹣3)2=14,
故选:A.
5.解:∵x=0.61时,x2+x﹣1=﹣0.0179;x=0.62时,x2+x﹣1=0.0044,
∴方程x2+x﹣1=0一个解x的范围为0.61<x<0.62.
故选C.
6.解:根据题意,将x=﹣2代入方程x2+ax﹣a2=0,得:
4﹣3a﹣a2=0,即a2+3a﹣4=0,
左边因式分解得:(a﹣1)(a+4)=0,
∴a﹣1=0,或a+4=0,
解得:a=1或﹣4,
故选:C.
7.解:∵关于x的一元二次方程(k﹣1)x2+4x+1=0有两个不相等的实数根,
∴,即,
解得:k<5且k≠1.
故选B.
8.解:由题意得:100(1﹣x)2=81,
故选:A.
9.解:﹣3x2+5x﹣1=0,
b2﹣4ac=52﹣4×(﹣3)×(﹣1)=13,
x==,
故选C.
10.解:依题意得(a+b)2=b(b+a+b),
而a=1,
∴b2﹣b﹣1=0,
∴b=,而b不能为负,
∴b=.
故选B.
二、填空题(每小题3分,共24分)
11.解:∵关于x的方程(x+1)2=1﹣k没有实根,
∴1﹣k<0,即k>1,
又∵k为整数,
∴k可以取2,
故答案为:2(答案不唯一).
12.解:∵(a﹣2)x2+(a﹣1)x﹣3=0是关于x的一元二次方程,
∴a满足的条件是:a≠2.
故答案为:a≠2.
13.解:∵m是关于x的方程x2﹣2x﹣3=0的一个根,
∴m2﹣2m﹣3=0,
∴m2﹣2m=3,
∴2m2﹣4m=6,
故答案为:6.
14.解:由方程x2﹣8x+15=0得:(x﹣3)(x﹣5)=0,
∴x﹣3=0或x﹣5=0,
解得:x=3或x=5,
当等腰三角形的三边长为9、9、3时,其周长为21;
当等腰三角形的三边长为9、9、5时,其周长为23;
当等腰三角形的三边长为9、3、3时,3+3<9,不符合三角形三边关系定理,舍去;
当等腰三角形的三边长为9、5、5时,其周长为19;
综上,该等腰三角形的周长为19或21或23,
故答案为:19或21或23.
15.解:设小道进出口的宽度为xm,
根据题意,得:30×20﹣20×2x﹣30x+2x x=532,
整理,得:x2﹣35x+34=0.
故答案为:x2﹣35x+34=0.
16.解:∵x1、x2是方程x2﹣4x+m=0的两个根,
∴x1+x2=﹣=4,x1x2==m.
∵x1+x2﹣x1x2=4﹣m=1,
∴m=3.
故答案为:4;3.
17.解:根据题意得x2﹣2 (﹣2x)+3=﹣1,
整理得x2+4x+4=0,
(x+2)2=0,
所以x1=x2=﹣2.
故答案为﹣2.
18.解:∵x2﹣x﹣1=0,
∴x2=x+1,
∴x4﹣3x+2016=(x+1)2﹣3x+2016
=x2+2x+1﹣3x+2016
=x2﹣x+2017
=1+2017
=2018,
故答案为2018.
三.解答题(共46分)
19.解:(1)方程整理得:(x﹣2)2=9,
开方得:x﹣2=3或x﹣2=﹣3,
解得:x=5或x=﹣1;
(2)方程配方得:x2﹣2x+1=200,即(x﹣1)2=200,
开方得:x﹣1=±10,
解得:x=1+10或x=1﹣10.
(3)3x(x﹣1)﹣2(x﹣1)=0,
(x﹣1)(3x﹣2)=0,
x﹣1=0或3x﹣2=0,
所以x1=1,x2=;
(4)(x+1)(x+2)=0,
x+1=0或x+2=0,
所以x1=﹣1,x2=﹣2.
20.解:设每一轮感染中平均每台电脑会感染x台电脑.
根据题意得:(1+x)2=81,
解得:x=8或x=﹣10(舍去).
答:每轮感染中平均一台电脑会感染8台电脑.
21.解:(1)小明解方程的方法是配方法,他的求解过程从第②步开始出现错误,这一步的运算依据应该是等式的基本性质;
故答案为:配方法,②,等式的基本性质;
(2)x2﹣4x=1,
x2﹣4x+4=1+4,
(x﹣2)2=5,
x﹣2=,
x=2±,
∴x1=2+,x2=2﹣.
22.解:(1)∵方程没有实数根,
∴b2﹣4ac=[﹣2(m+1)]2﹣4m2=8m+4<0,
∴m<﹣,
∴当m<﹣时,原方程没有实数根;
(2)由(1)可知,当m≥﹣时,方程有实数根,
当m=1时,原方程变为x2﹣4x+1=0,
设此时方程的两根分别为x1,x2,
解得x1=2+,x2=2﹣.
23.解:设该单位这次共有x名员工去长寿山看红叶,则人均费用是[50﹣(x﹣25)]元
由题意得[50﹣(x﹣25)]x=1350,
整理得x2﹣75x+1350=0,
解得x1=45,x2=30.
当x=45时,人均门票价格为50﹣(x﹣25)=30<35,不合题意,应舍去.
当x=30时,人均旅游费用为50﹣(x﹣25)=45>35,符合题意.
答:该单位这次共有30名员工去长寿山看红叶.
24.解:(1)∵大正方形的边长是[x+(x﹣2)],
∴大正方形面积是:[x+(x﹣2)]2=(2x﹣2)2;
∵小正方形的边长是:[x+(x﹣2)]﹣2(x﹣2)=2,长方形的面积为3
又∵大正方形面积等于四个长方形与小正方形面积之和,
∴(2x﹣2)2=4×3+22=16;
故答案为:(2x﹣2)2;(2x﹣2)2=4×3+22;
(2)第一步:将原方程变形为x2﹣x=1,即x(x﹣1)=1.
第二步:构造一个长为x,宽为(x﹣1)的长方形,长比宽大1,且面积为1.
第三步:用四个这样的长方形围成一个大正方形,中间是一个小正方形.
第四步:计算大正方形面积用x表示为[x+(x+1)]2.
由观察可得,大正方形面积等于四个长方形与小正方形面积之和,得方程[x+(x﹣1)]2=4×1+12,两边开方可求得:x1=,x2=.
第2单元 一元二次方程
满分100分
时间100分钟
班级
姓名
一、选择题(每小题3分,共30分)
1.(2016秋 吴中区期末)一元二次方程:x2﹣9=0的解是( )
A.3
B.﹣3
C.±3
D.9
2.(2016 新都区模拟)下列方程中,关于x的一元二次方程是( )
A.(x+1)2=2(x+1)
B.
C.ax2+bx+c=0
D.x2+2x=x2﹣1
3.(2016 武汉校级模拟)将一元二次方程4x2+7=3x化成一般式后,二次项系数和一次项系数分别为( )
A.4,3
B.4,7
C.4,﹣3
D.4x2,﹣3x
4.(2016 新疆)一元二次方程x2﹣6x﹣5=0配方可变形为( )
A.(x﹣3)2=14
B.(x﹣3)2=4
C.(x+3)2=14
D.(x+3)2=4
5.(2016秋 简阳市期末)根据下列表格的对应值:
0.59
0.60
0.61
0.62
0.63
x2+x﹣1
﹣0.0619
﹣0.04
﹣0.0179
0.0044
0.0269
判断方程x2+x﹣1=0一个解的取值范围是( )
A.0.59<x<0.61
B.0.60<x<0.61
C.0.61<x<0.62
D.0.62<x<0.63
6.(2016 攀枝花)若x=﹣2是关于x的一元二次方程x2+ax﹣a2=0的一个根,则a的值为( )
A.﹣1或4
B.﹣1或﹣4
C.1或﹣4
D.1或4
7.(2016 桂林)若关于x的一元二次方程(k﹣1)x2+4x+1=0有两个不相等的实数根,则k的取值范围是( )
A.k<5
B.k<5,且k≠1
C.k≤5,且k≠1
D.k>5
8.(2017 曲靖一模)为解决群众看病贵的问题,有关部门决定降低药价,对某种原价为100元的药品进行连续两次降价后为81元.设平均每次降价的百分率为x,则下列方程正确的是( )
A.100(1﹣x)2=81
B.81(1﹣x)2=100
C.100(1﹣2x)=81
D.81(1﹣2x)=100
9.(2016秋 鼓楼区校级期中)用公式解方程﹣3x2+5x﹣1=0,正确的是( )
A.x=
B.x=
C.x=
D.x=
10.(2016 张家口一模)如图,若将左图正方形剪成四块,恰能拼成右图的矩形,设a=1,则b=( )
A.
B.
C.
D.
二、填空题(每小题3分,共24分)
11.(2017 曲靖一模)若k为整数,且关于x的方程(x+1)2=1﹣k没有实根,则满足条件的k的值为
(只需写一个)
12.(2016 洪泽县一模)已知(a﹣2)x2+(a﹣1)x﹣3=0是关于x的一元二次方程,则a满足的条件是
.
13.(2016 菏泽)已知m是关于x的方程x2﹣2x﹣3=0的一个根,则2m2﹣4m=
.
14.(2016 随州)已知等腰三角形的一边长为9,另一边长为方程x2﹣8x+15=0的根,则该等腰三角形的周长为
.
15.(2016秋 南京期中)如图,某单位准备将院内一块长30m,宽20m的长方形花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图,要使种植花草的面积为532m2,设小道进出口的宽度为x
m,根据条件,可列出方程:
.
16.(2016 南京)设x1、x2是方程x2﹣4x+m=0的两个根,且x1+x2﹣x1x2=1,则x1+x2=
,m=
.
17.(2016秋 黄陂区期中)小明设计了一个魔术盒,当任意实数对(a,b)进入其中,会得到一个新的实数a2﹣2b+3.若将实数(x,﹣2x)放入其中,得到﹣1,则x=
.
18.(2016 句容市一模)将关于x的一元二次方程x2+bx+c=0变形为x2=﹣bx﹣c,就可得x2表示为关于x的一次多项式,从而达到“降次”的目的,我们称这样的方法为“降次法”.已知x2﹣x﹣1=0,可用“降次法”求得x4﹣3x+2016的值是
.
三.解答题(共46分)
19.(2016秋 仁寿县期中)用适当的方法解下列方程(12分)
(1)(x﹣2)2﹣9=0
(2)x2﹣2x﹣199=0.
(3)3x(x﹣1)=2x﹣2
(4)x2+3x+2=0.
20.(2016 新都区模拟)某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?(6分)
21.(2016秋 宁德期末)小明同学解一元二次方程x2﹣4x﹣1=0的过程如图所示(6分)
解:x2﹣4x=1…①
x2﹣4x+4=1
…②
(x﹣2)2=1…③
x﹣2=±1…④
x1=3,x2=1…⑤
(1)小明解方程的方法是
,他的求解过程从第
步开始出现错误,这一步的运算依据应该是
;
(2)解这个方程.
22.(2016 郑州模拟)已知关于x的方程x2﹣2(m+1)x+m2=0.(6分)
(1)当m取什么值时,原方程没有实数根;
(2)对m选取一个合适的非零整数,使原方程有两个不相等的实数根,并求出这两个实数根.
23.(2017 郑州一模)巩义长寿山景区门票价格为50元,在今年红叶节期问,为吸引游客,推出了如下优惠活动:如果人数不超过25人,门票按原价销售,如果人数超过25人,每超过1人,所购买的门票均降低1元,但人均门票不低于35元,某单位组织员工去长寿山看红叶,共支付门票费用1350元,请问该单位这次共有多少名员工去长寿山看红叶?(8分)
24.(2016 虞城县三模)你知道古代数学家怎样解一元二次方程吗?以x2﹣2x﹣3=0为例,大致过程如下:(8分)
第一步:将原方程变形为x2﹣2x=3,即x(x﹣2)=3.
第二步:构造一个长为x,宽为(x﹣2)的长方形,长比宽大2,且面积为3,如图1所示.
第三步:用四个这样的长方形围成一个大正方形,中间是一个小正方形,如图2所示.
第四步:计算大正方形面积用x表示为
.
由观察可得,大正方形面积等于四个长方形与小正方形面积之和,得方程
,两边开方可求得:x1=3,x2=﹣1.
(1)第四步中横线上应填入
;
.
(2)请参考古人的思考过程,解方程x2﹣x﹣1=0.
参考答案
一、选择题(每小题3分,共30分)
1.解:∵x2=9,
∴x=3或x=﹣3,
故选:C.
2.解:下列方程中,关于x的一元二次方程是(x+1)2=2(x+1),
故选A.
3.解:4x2+7=3x,
4x2﹣3x+7=0,
二次项系数和一次项系数分别为4、﹣3,
故选C.
4.解:x2﹣6x﹣5=0,
x2﹣6x=5,
x2﹣6x+9=5+9,
(x﹣3)2=14,
故选:A.
5.解:∵x=0.61时,x2+x﹣1=﹣0.0179;x=0.62时,x2+x﹣1=0.0044,
∴方程x2+x﹣1=0一个解x的范围为0.61<x<0.62.
故选C.
6.解:根据题意,将x=﹣2代入方程x2+ax﹣a2=0,得:
4﹣3a﹣a2=0,即a2+3a﹣4=0,
左边因式分解得:(a﹣1)(a+4)=0,
∴a﹣1=0,或a+4=0,
解得:a=1或﹣4,
故选:C.
7.解:∵关于x的一元二次方程(k﹣1)x2+4x+1=0有两个不相等的实数根,
∴,即,
解得:k<5且k≠1.
故选B.
8.解:由题意得:100(1﹣x)2=81,
故选:A.
9.解:﹣3x2+5x﹣1=0,
b2﹣4ac=52﹣4×(﹣3)×(﹣1)=13,
x==,
故选C.
10.解:依题意得(a+b)2=b(b+a+b),
而a=1,
∴b2﹣b﹣1=0,
∴b=,而b不能为负,
∴b=.
故选B.
二、填空题(每小题3分,共24分)
11.解:∵关于x的方程(x+1)2=1﹣k没有实根,
∴1﹣k<0,即k>1,
又∵k为整数,
∴k可以取2,
故答案为:2(答案不唯一).
12.解:∵(a﹣2)x2+(a﹣1)x﹣3=0是关于x的一元二次方程,
∴a满足的条件是:a≠2.
故答案为:a≠2.
13.解:∵m是关于x的方程x2﹣2x﹣3=0的一个根,
∴m2﹣2m﹣3=0,
∴m2﹣2m=3,
∴2m2﹣4m=6,
故答案为:6.
14.解:由方程x2﹣8x+15=0得:(x﹣3)(x﹣5)=0,
∴x﹣3=0或x﹣5=0,
解得:x=3或x=5,
当等腰三角形的三边长为9、9、3时,其周长为21;
当等腰三角形的三边长为9、9、5时,其周长为23;
当等腰三角形的三边长为9、3、3时,3+3<9,不符合三角形三边关系定理,舍去;
当等腰三角形的三边长为9、5、5时,其周长为19;
综上,该等腰三角形的周长为19或21或23,
故答案为:19或21或23.
15.解:设小道进出口的宽度为xm,
根据题意,得:30×20﹣20×2x﹣30x+2x x=532,
整理,得:x2﹣35x+34=0.
故答案为:x2﹣35x+34=0.
16.解:∵x1、x2是方程x2﹣4x+m=0的两个根,
∴x1+x2=﹣=4,x1x2==m.
∵x1+x2﹣x1x2=4﹣m=1,
∴m=3.
故答案为:4;3.
17.解:根据题意得x2﹣2 (﹣2x)+3=﹣1,
整理得x2+4x+4=0,
(x+2)2=0,
所以x1=x2=﹣2.
故答案为﹣2.
18.解:∵x2﹣x﹣1=0,
∴x2=x+1,
∴x4﹣3x+2016=(x+1)2﹣3x+2016
=x2+2x+1﹣3x+2016
=x2﹣x+2017
=1+2017
=2018,
故答案为2018.
三.解答题(共46分)
19.解:(1)方程整理得:(x﹣2)2=9,
开方得:x﹣2=3或x﹣2=﹣3,
解得:x=5或x=﹣1;
(2)方程配方得:x2﹣2x+1=200,即(x﹣1)2=200,
开方得:x﹣1=±10,
解得:x=1+10或x=1﹣10.
(3)3x(x﹣1)﹣2(x﹣1)=0,
(x﹣1)(3x﹣2)=0,
x﹣1=0或3x﹣2=0,
所以x1=1,x2=;
(4)(x+1)(x+2)=0,
x+1=0或x+2=0,
所以x1=﹣1,x2=﹣2.
20.解:设每一轮感染中平均每台电脑会感染x台电脑.
根据题意得:(1+x)2=81,
解得:x=8或x=﹣10(舍去).
答:每轮感染中平均一台电脑会感染8台电脑.
21.解:(1)小明解方程的方法是配方法,他的求解过程从第②步开始出现错误,这一步的运算依据应该是等式的基本性质;
故答案为:配方法,②,等式的基本性质;
(2)x2﹣4x=1,
x2﹣4x+4=1+4,
(x﹣2)2=5,
x﹣2=,
x=2±,
∴x1=2+,x2=2﹣.
22.解:(1)∵方程没有实数根,
∴b2﹣4ac=[﹣2(m+1)]2﹣4m2=8m+4<0,
∴m<﹣,
∴当m<﹣时,原方程没有实数根;
(2)由(1)可知,当m≥﹣时,方程有实数根,
当m=1时,原方程变为x2﹣4x+1=0,
设此时方程的两根分别为x1,x2,
解得x1=2+,x2=2﹣.
23.解:设该单位这次共有x名员工去长寿山看红叶,则人均费用是[50﹣(x﹣25)]元
由题意得[50﹣(x﹣25)]x=1350,
整理得x2﹣75x+1350=0,
解得x1=45,x2=30.
当x=45时,人均门票价格为50﹣(x﹣25)=30<35,不合题意,应舍去.
当x=30时,人均旅游费用为50﹣(x﹣25)=45>35,符合题意.
答:该单位这次共有30名员工去长寿山看红叶.
24.解:(1)∵大正方形的边长是[x+(x﹣2)],
∴大正方形面积是:[x+(x﹣2)]2=(2x﹣2)2;
∵小正方形的边长是:[x+(x﹣2)]﹣2(x﹣2)=2,长方形的面积为3
又∵大正方形面积等于四个长方形与小正方形面积之和,
∴(2x﹣2)2=4×3+22=16;
故答案为:(2x﹣2)2;(2x﹣2)2=4×3+22;
(2)第一步:将原方程变形为x2﹣x=1,即x(x﹣1)=1.
第二步:构造一个长为x,宽为(x﹣1)的长方形,长比宽大1,且面积为1.
第三步:用四个这样的长方形围成一个大正方形,中间是一个小正方形.
第四步:计算大正方形面积用x表示为[x+(x+1)]2.
由观察可得,大正方形面积等于四个长方形与小正方形面积之和,得方程[x+(x﹣1)]2=4×1+12,两边开方可求得:x1=,x2=.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
