《4.5三角形中位线》同步练习含答案
图片预览


文档简介
《三角形中位线》同步练习题
选择题
1.△ABC中,D、E分别是AB、AC边上的中点,若BC=8,则DE等于(
)
A.
5
B.
4
C.
3
D.
2
2.三角形的三条中位线长分别为3cm,4cm,6cm,则原三角形的周长为(
)
A.
6.
5cm
B.
34cm
C
26cm
D.
52cm
3.如图,在四边形ABCD
中,AB=CD,M,N,P分别AD,BC,BD的中点,若∠MPN=130°,则∠NMP=(
)
A.
25°
B.
30°
C.
35°
D.
50°
第3题
第4题
4.如图所示,已知点E、F分别是△ABC中AC、AB边的中点,BE、CF相交于点G,FG=3,则CF的长为(
)
A.4
B.4.5
C.6
D.9
二、填空题
5.
已知三角形的各边分别为8cm,10cm,12cm,以各边中点为顶点的三角形的周长是_______。
7题
8题
6.顺次连结任意四边形各边中点所得到的四边形一定是__
___.
7.在四边形ABCD中,AC=6cm,BD=8cm,分别是边的中点,则四边形EFGH的周长为
.
8.
如图,A、B两处被池塘隔开,为了测量A、B两处的距离,在AB外选一适当的点C,连接AC、BC,并分别取线段AC、BC的中点E、F,测得EF=22m,则AB=__________m.
三、证明题:
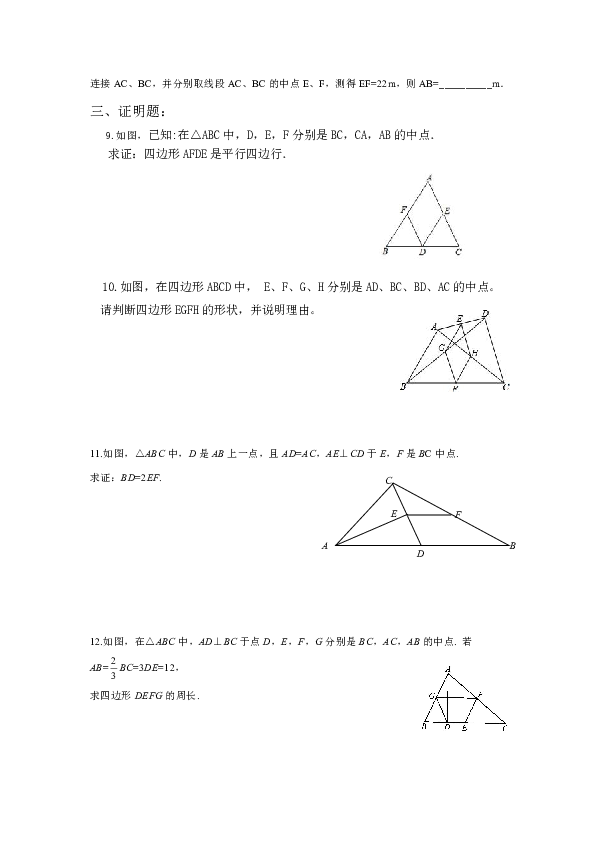
9.如图,已知:在△ABC中,D,E,F分别是BC,CA,AB的中点.
求证:四边形AFDE是平行四边行.
10.如图,在四边形ABCD中,
E、F、G、H分别是AD、BC、BD、AC的中点。
请判断四边形EGFH的形状,并说明理由。
11.如图,△ABC中,D是AB上一点,且AD=AC,AE⊥CD于E,F是BC中点.
求证:BD=2EF.
12.如图,在△ABC中,AD⊥BC于点D,E,F,G分别是BC,AC,AB的中点.
若AB=BC=3DE=12,
求四边形DEFG的周长.
参考答案
一、选择题1.答案:C
2.答案:C
3.
答案:A
4.答案:D
二、填空题5.答案:17;6.答案:平行四边形;7.答案:14cm;8.答案:44..
三、证明题
9.答案:8
解析:【解答】过D作DG∥AB交BC于G,∵AD∥BC,AB∥DG,
∴四边形ABGD是平行四边形,∴AB=DG.
∵EF∥AB,∴EF∥DG,∵DE=CE,∴GF=CF.
∴EF是△CDG的中位线,∴EF=DG.
∴DG=2EF=8,即AB=8.
10.答案:证明过程见解析.
解析:【解答】证明:∵AD=AC,AE⊥CD,∴CE=DE.
又∵F是BC中点,∴BD=2EF.
11.答案:证明过程见解析.
解析:【解答】证明:延长CD与BA交于F点.
∵AD是∠BAC的外角平分线,∴∠CAD=∠EAD.
∵CD⊥AD,∴∠ADC=∠ADF=90°,∴∠ACD=∠F,
∴AC=AF,∴CD=DF.
∵E是BC的中点,∴DE=BF=(AB+AC).
12.答案:25
解析:【解答】∵AB=BC=3DE=12,∴BC=18,DE=4.
∵AD⊥BC,G是AB的中点,∴DG=AB=6.
∵E,F,G分别是BC,AC,AB的中点,
∴FG=BC=9,EF=AB=6.
∴四边形DEFG的周长为4+6+9+6=25.
A
F
E
C
B
G
A
B
C
D
E
F
G
H
F
E
D
C
B
A
F
选择题
1.△ABC中,D、E分别是AB、AC边上的中点,若BC=8,则DE等于(
)
A.
5
B.
4
C.
3
D.
2
2.三角形的三条中位线长分别为3cm,4cm,6cm,则原三角形的周长为(
)
A.
6.
5cm
B.
34cm
C
26cm
D.
52cm
3.如图,在四边形ABCD
中,AB=CD,M,N,P分别AD,BC,BD的中点,若∠MPN=130°,则∠NMP=(
)
A.
25°
B.
30°
C.
35°
D.
50°
第3题
第4题
4.如图所示,已知点E、F分别是△ABC中AC、AB边的中点,BE、CF相交于点G,FG=3,则CF的长为(
)
A.4
B.4.5
C.6
D.9
二、填空题
5.
已知三角形的各边分别为8cm,10cm,12cm,以各边中点为顶点的三角形的周长是_______。
7题
8题
6.顺次连结任意四边形各边中点所得到的四边形一定是__
___.
7.在四边形ABCD中,AC=6cm,BD=8cm,分别是边的中点,则四边形EFGH的周长为
.
8.
如图,A、B两处被池塘隔开,为了测量A、B两处的距离,在AB外选一适当的点C,连接AC、BC,并分别取线段AC、BC的中点E、F,测得EF=22m,则AB=__________m.
三、证明题:
9.如图,已知:在△ABC中,D,E,F分别是BC,CA,AB的中点.
求证:四边形AFDE是平行四边行.
10.如图,在四边形ABCD中,
E、F、G、H分别是AD、BC、BD、AC的中点。
请判断四边形EGFH的形状,并说明理由。
11.如图,△ABC中,D是AB上一点,且AD=AC,AE⊥CD于E,F是BC中点.
求证:BD=2EF.
12.如图,在△ABC中,AD⊥BC于点D,E,F,G分别是BC,AC,AB的中点.
若AB=BC=3DE=12,
求四边形DEFG的周长.
参考答案
一、选择题1.答案:C
2.答案:C
3.
答案:A
4.答案:D
二、填空题5.答案:17;6.答案:平行四边形;7.答案:14cm;8.答案:44..
三、证明题
9.答案:8
解析:【解答】过D作DG∥AB交BC于G,∵AD∥BC,AB∥DG,
∴四边形ABGD是平行四边形,∴AB=DG.
∵EF∥AB,∴EF∥DG,∵DE=CE,∴GF=CF.
∴EF是△CDG的中位线,∴EF=DG.
∴DG=2EF=8,即AB=8.
10.答案:证明过程见解析.
解析:【解答】证明:∵AD=AC,AE⊥CD,∴CE=DE.
又∵F是BC中点,∴BD=2EF.
11.答案:证明过程见解析.
解析:【解答】证明:延长CD与BA交于F点.
∵AD是∠BAC的外角平分线,∴∠CAD=∠EAD.
∵CD⊥AD,∴∠ADC=∠ADF=90°,∴∠ACD=∠F,
∴AC=AF,∴CD=DF.
∵E是BC的中点,∴DE=BF=(AB+AC).
12.答案:25
解析:【解答】∵AB=BC=3DE=12,∴BC=18,DE=4.
∵AD⊥BC,G是AB的中点,∴DG=AB=6.
∵E,F,G分别是BC,AC,AB的中点,
∴FG=BC=9,EF=AB=6.
∴四边形DEFG的周长为4+6+9+6=25.
A
F
E
C
B
G
A
B
C
D
E
F
G
H
F
E
D
C
B
A
F
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
