3.2中位数和众数同步练习题(附答案)
图片预览

文档简介
第三章数据分析初步3.2
中位数和众数
一、选择题
1.在一次歌咏比赛中,某选手的得分情况如下:92,88,95,93,96,95,94.这组数据的众数和中位数分别是
(
)
A.94,94
B.95,95
C.94,95
D.95,94
2.一组数据1,2,a的平均数为2,另一组数据﹣l,a,1,2,b的唯一众数为﹣l,则数据﹣1,a,1,2,b的中位数为(
)
A.1
B.2
C.3
D.-1
3.在某次体育测试中,九(1)班6位同学的立定跳远成绩(单位:m)分别为:1.71,1.85,1.85,1.95,2.10,2.31,则这组数据的众数是
(
)
A.1.71
B.1.85
C.1.90
D.2.31
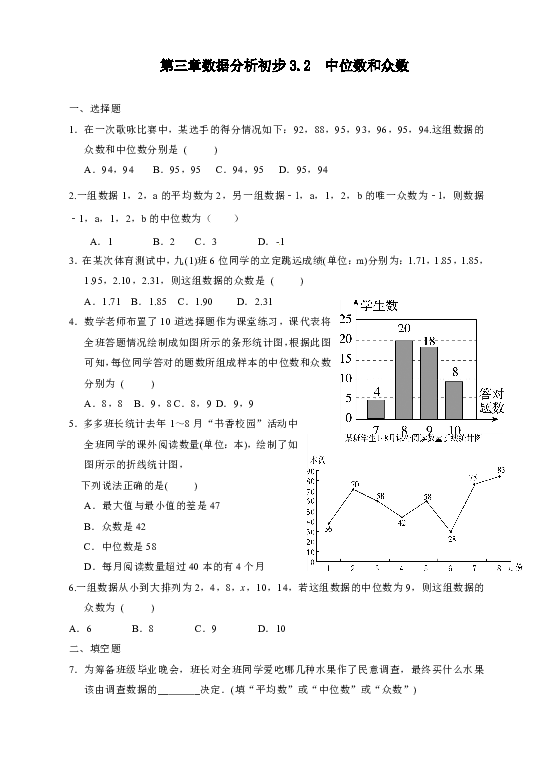
4.数学老师布置了10道选择题作为课堂练习,课代表将全班答题情况绘制成如图所示的条形统计图,根据此图可知,每位同学答对的题数所组成样本的中位数和众数分别为
(
)
A.8,8
B.9,8
C.8,9
D.9,9
5.多多班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图所示的折线统计图,
下列说法正确的是(
)
A.最大值与最小值的差是47
B.众数是42
C.中位数是58
D.每月阅读数量超过40本的有4个月
6.一组数据从小到大排列为2,4,8,x,10,14,若这组数据的中位数为9,则这组数据的众数为
(
)
A.6
B.8
C.9
D.10
二、填空题
7.为筹备班级毕业晚会,班长对全班同学爱吃哪几种水果作了民意调查,最终买什么水果该由调查数据的__
_决定.(填“平均数”或“中位数”或“众数”)
8.某品牌专卖店对上个月销售的男运动鞋尺码统计如下:
这组统计数据中的众数是__
__码.
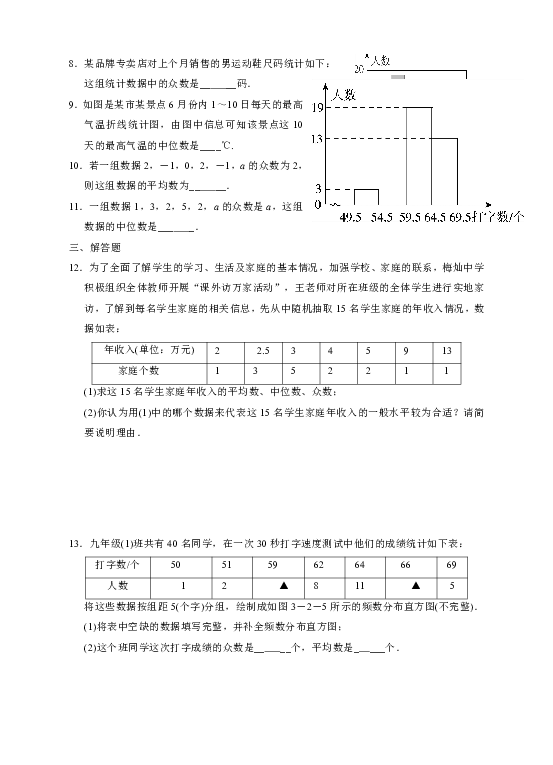
9.如图是某市某景点6月份内1~10日每天的最高气温折线统计图,由图中信息可知该景点这10天的最高气温的中位数是____℃.
10.若一组数据2,-1,0,2,-1,a的众数为2,则这组数据的平均数为__
__.
11.一组数据1,3,2,5,2,a的众数是a,这组数据的中位数是___
_.
三、解答题
12.为了全面了解学生的学习、生活及家庭的基本情况,加强学校、家庭的联系,梅灿中学积极组织全体教师开展“课外访万家活动”,王老师对所在班级的全体学生进行实地家访,了解到每名学生家庭的相关信息,先从中随机抽取15名学生家庭的年收入情况,数据如表:
年收入(单位:万元)
2
2.5
3
4
5
9
13
家庭个数
1
3
5
2
2
1
1
(1)求这15名学生家庭年收入的平均数、中位数、众数;
(2)你认为用(1)中的哪个数据来代表这15名学生家庭年收入的一般水平较为合适?请简要说明理由.
13.九年级(1)班共有40名同学,在一次30秒打字速度测试中他们的成绩统计如下表:
打字数/个
50
51
59
62
64
66
69
人数
1
2
▲
8
11
▲
5
将这些数据按组距5(个字)分组,绘制成如图3-2-5所示的频数分布直方图(不完整).
(1)将表中空缺的数据填写完整,并补全频数分布直方图;
(2)这个班同学这次打字成绩的众数是__
__个,平均数是_
___个.
14.在喜迎建党九十周年之际,某校举办校园唱红歌比赛,选出10名同学担任评委,从如下四种方案中选择合理方案来确定演唱者的最后得分(每个评委打分最高10分).
方案1:所有评委给分的平均分;
方案2:在所有评委中,去掉一个最高分和一个最低分,再计算剩余评委的平均分;
方案3:所有评委给分的中位数;
方案4:所有评委给分的众数.
为了探究上述方案的合理性,先对某个同学的演唱成绩进行统计实验,下图是这个同学的得分统计图:
(1)分别按上述四种方案计算这个同学演唱的最后得分;
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适合作为这个同学演唱的最后得分
中位数和众数答案
1、B2、D3、B4、B5、C6、D
7、众数8、419、1010、11、2
12、平均数4.3万元将这15个数据从小到大排列,最中间的数是3,
所以中位数是3万元;
在这一组数据中3是出现次数最多的,故众数是3万元.
(2)众数代表这15名学生家庭年收入的一般水平较为合适,因为3出现的次数最多,所以能代表家庭年收入的一般水平.
13、解:(1)表中空缺的数据依次为5,8.
补全频数分布直方图如答图所示.
(2)64 63
14、解:
(1)方案1最后得分为(3.2+7.0+7.8+3×8+3×8.4+9.8)=7.7;
方案2最后得分为(7.0+7.8+3×8+3×8.4)=8;
方案3最后得分为8;
方案4最后得分为8或8.4.
(2)因为方案1中的平均数受极端数值的影响,不能反映这组数据的“平均水平”,所以方案1不适合作为最后得分的方案.
因为方案4中的众数有两个,众数失去了实际意义,所以方案4不适合作为最后得分的方案.
中位数和众数
一、选择题
1.在一次歌咏比赛中,某选手的得分情况如下:92,88,95,93,96,95,94.这组数据的众数和中位数分别是
(
)
A.94,94
B.95,95
C.94,95
D.95,94
2.一组数据1,2,a的平均数为2,另一组数据﹣l,a,1,2,b的唯一众数为﹣l,则数据﹣1,a,1,2,b的中位数为(
)
A.1
B.2
C.3
D.-1
3.在某次体育测试中,九(1)班6位同学的立定跳远成绩(单位:m)分别为:1.71,1.85,1.85,1.95,2.10,2.31,则这组数据的众数是
(
)
A.1.71
B.1.85
C.1.90
D.2.31
4.数学老师布置了10道选择题作为课堂练习,课代表将全班答题情况绘制成如图所示的条形统计图,根据此图可知,每位同学答对的题数所组成样本的中位数和众数分别为
(
)
A.8,8
B.9,8
C.8,9
D.9,9
5.多多班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图所示的折线统计图,
下列说法正确的是(
)
A.最大值与最小值的差是47
B.众数是42
C.中位数是58
D.每月阅读数量超过40本的有4个月
6.一组数据从小到大排列为2,4,8,x,10,14,若这组数据的中位数为9,则这组数据的众数为
(
)
A.6
B.8
C.9
D.10
二、填空题
7.为筹备班级毕业晚会,班长对全班同学爱吃哪几种水果作了民意调查,最终买什么水果该由调查数据的__
_决定.(填“平均数”或“中位数”或“众数”)
8.某品牌专卖店对上个月销售的男运动鞋尺码统计如下:
这组统计数据中的众数是__
__码.
9.如图是某市某景点6月份内1~10日每天的最高气温折线统计图,由图中信息可知该景点这10天的最高气温的中位数是____℃.
10.若一组数据2,-1,0,2,-1,a的众数为2,则这组数据的平均数为__
__.
11.一组数据1,3,2,5,2,a的众数是a,这组数据的中位数是___
_.
三、解答题
12.为了全面了解学生的学习、生活及家庭的基本情况,加强学校、家庭的联系,梅灿中学积极组织全体教师开展“课外访万家活动”,王老师对所在班级的全体学生进行实地家访,了解到每名学生家庭的相关信息,先从中随机抽取15名学生家庭的年收入情况,数据如表:
年收入(单位:万元)
2
2.5
3
4
5
9
13
家庭个数
1
3
5
2
2
1
1
(1)求这15名学生家庭年收入的平均数、中位数、众数;
(2)你认为用(1)中的哪个数据来代表这15名学生家庭年收入的一般水平较为合适?请简要说明理由.
13.九年级(1)班共有40名同学,在一次30秒打字速度测试中他们的成绩统计如下表:
打字数/个
50
51
59
62
64
66
69
人数
1
2
▲
8
11
▲
5
将这些数据按组距5(个字)分组,绘制成如图3-2-5所示的频数分布直方图(不完整).
(1)将表中空缺的数据填写完整,并补全频数分布直方图;
(2)这个班同学这次打字成绩的众数是__
__个,平均数是_
___个.
14.在喜迎建党九十周年之际,某校举办校园唱红歌比赛,选出10名同学担任评委,从如下四种方案中选择合理方案来确定演唱者的最后得分(每个评委打分最高10分).
方案1:所有评委给分的平均分;
方案2:在所有评委中,去掉一个最高分和一个最低分,再计算剩余评委的平均分;
方案3:所有评委给分的中位数;
方案4:所有评委给分的众数.
为了探究上述方案的合理性,先对某个同学的演唱成绩进行统计实验,下图是这个同学的得分统计图:
(1)分别按上述四种方案计算这个同学演唱的最后得分;
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适合作为这个同学演唱的最后得分
中位数和众数答案
1、B2、D3、B4、B5、C6、D
7、众数8、419、1010、11、2
12、平均数4.3万元将这15个数据从小到大排列,最中间的数是3,
所以中位数是3万元;
在这一组数据中3是出现次数最多的,故众数是3万元.
(2)众数代表这15名学生家庭年收入的一般水平较为合适,因为3出现的次数最多,所以能代表家庭年收入的一般水平.
13、解:(1)表中空缺的数据依次为5,8.
补全频数分布直方图如答图所示.
(2)64 63
14、解:
(1)方案1最后得分为(3.2+7.0+7.8+3×8+3×8.4+9.8)=7.7;
方案2最后得分为(7.0+7.8+3×8+3×8.4)=8;
方案3最后得分为8;
方案4最后得分为8或8.4.
(2)因为方案1中的平均数受极端数值的影响,不能反映这组数据的“平均水平”,所以方案1不适合作为最后得分的方案.
因为方案4中的众数有两个,众数失去了实际意义,所以方案4不适合作为最后得分的方案.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
