3.3由三视图描述几何体同步练习题(附答案)
文档属性
| 名称 | 3.3由三视图描述几何体同步练习题(附答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 376.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-20 00:00:00 | ||
图片预览

文档简介
由三视图描述几何体
班级:___________姓名:___________得分:__________
选择题(每小题10分,40分)
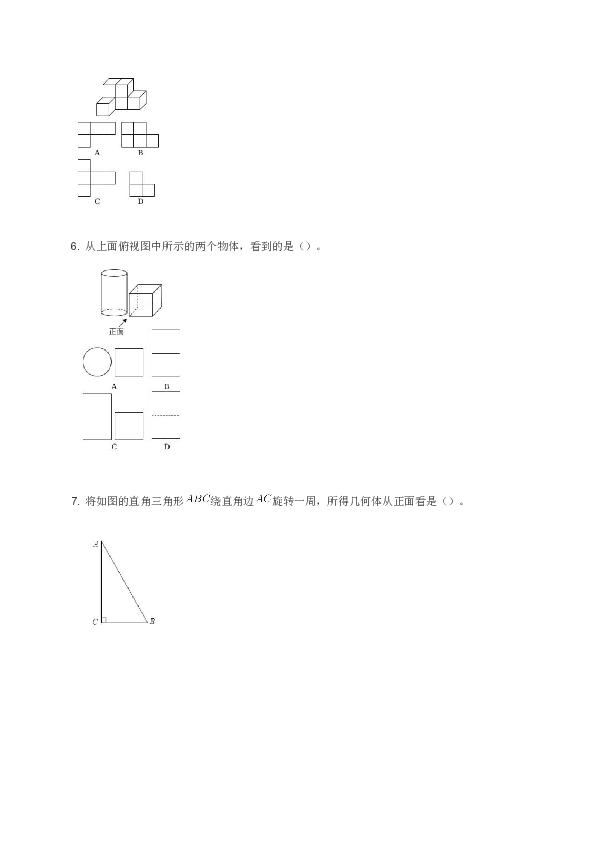
1.以下关于几何体的三视图的论述中,正确的是(
).
A.球的三视图总是三个全等的圆
B.正方体的三视图总是三个全等的正方形
C.水平放置的正四面体的三视图都是正三角形
D.水平放置的圆台的俯视图是一个圆
2.将长方体截去一个四棱锥,得到的几何体如下图所示,则该几何体的左视图为(
).
3.一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是(
)
(A)球
(B)三棱锥
(C)正方体
(D)圆柱
4.如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为________.
如图,是由六个小正方体组合而成的一个立体图形,它的主视图是(
)。
6.
从上面俯视图中所示的两个物体,看到的是()。
7.
将如图的直角三角形绕直角边旋转一周,所得几何体从正面看是()。
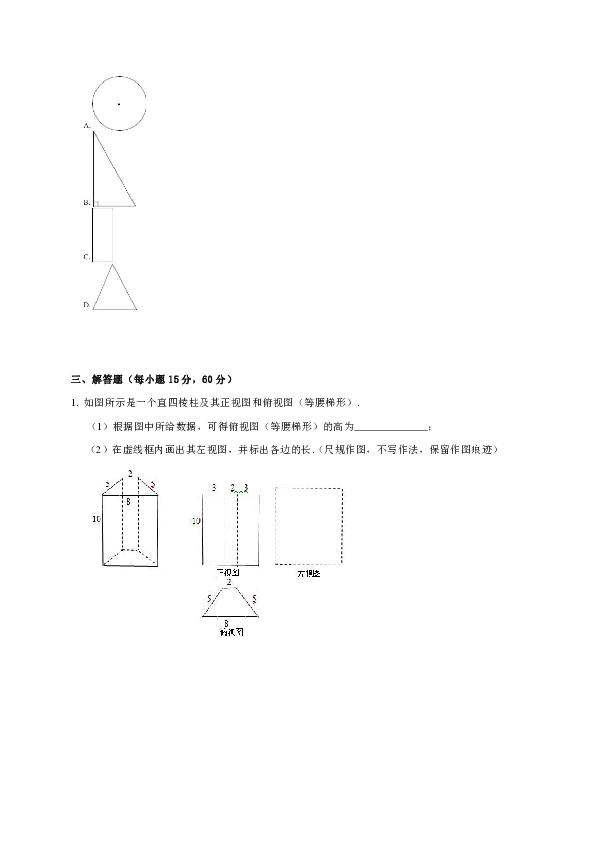
三、解答题(每小题15分,60分)
1.
如图所示是一个直四棱柱及其正视图和俯视图(等腰梯形).
(1)根据图中所给数据,可得俯视图(等腰梯形)的高为
;
(2)在虚线框内画出其左视图,并标出各边的长.(尺规作图,不写作法,保留作图痕迹)
2.
已知物体三视图的外轮廓,如何构思该物体?
3.用小方块搭一个几何体,使得它的主视图和俯视图如图所示,这样的几何体只有一种吗
4、一几何体按比例绘制的三视图如图所示(单位:m):
(1)试画出它的直观图;
(2)求它的表面积和体积.
参考答案
选择题
A
【解析】画几何体的三视图要考虑视角,但对于球无论选择怎样的视角,其三视图总是三个全等的圆.答案A
2.
D
【解析】被截去的四棱锥的三条可见侧棱中有两条为长方体的面对角线,它们在右侧面上的投影与右侧面(长方形)的两条边重合,另一条为体对角线,它在右侧面上的投影与右侧面的对角线重合,对照各图,只有选项D符合.答案:D
3. D
【解析】一般地,圆柱的正视图是矩形,侧视图是矩形,而俯视图是圆.而球、正方体、三棱锥的三视图形状都相同,大小均相等是可以的,故选D.
4.
2
【解析】(构造法)由主视图和俯视图可知几何体是正方体切割后的一部分(四棱锥C1-
ABCD),还原在正方体中,如图所示.多面体最长的一条棱即为正方体的体对角线,如图即AC1.由正方体棱长AB=2知最长棱AC1的长为2.答案是2
【点评】
构造正方体,本题就很容易得出结论,此种方法在立体几何问题中较为常见,把抽象问题转化为直观问题解决.
B
【解析】主视图是在正面从前向后观察物体得到的图形。从前向后观察物体得到的图形含有三列两行,从左到右每列的正方形的个数是2、2、1,从下到上的每行的正方形的个数是3、2。
故本题正确答案为B。
A
【解析】由于正方体的俯视图是个正方形,而竖着的圆柱体的俯视图是个圆形,因此只有A的图形符合这个条件。故选A.
D
【解析】先根据旋转的性质可得直角三角形ABC绕直角边AC旋转一周可得到的几何体为圆锥,再根据圆锥的正视图即可作出判断。
∵直角三角形ABC绕直角边AC旋转一周得到的几何体为圆锥
∴所得几何体从正面看是等腰三角形
故选D.
二、解答题
1.
解:(1)
4
(2)
2.
3.
4.
(1)直观图如图所示.
(2)由三视图可知该几何体是长方体被截去一个角,且该几何体的体积是以A1A,A1D1,A1B1为棱的长方体的体积的34,
在直角梯形AA1B1B中,作BE⊥A1B1于E,
则四边形AA1EB是正方形,
∴AA1=BE=1,
在Rt△BEB1中,BE=1,EB1=1,
∴BB1=2,
∴几何体的表面积
S=S正方形ABCD+S矩形A1B1C1D1+2S梯形AA1B1B+S矩形BB1C1C+S正方形AA1D1D
=1+2×1+2×12×(1+2)×1+1×2+1=7+2(m2).
∴几何体的体积V=34×1×2×1=32(m3),
∴该几何体的表面积为(7+2)
m2,体积为32
m3.
班级:___________姓名:___________得分:__________
选择题(每小题10分,40分)
1.以下关于几何体的三视图的论述中,正确的是(
).
A.球的三视图总是三个全等的圆
B.正方体的三视图总是三个全等的正方形
C.水平放置的正四面体的三视图都是正三角形
D.水平放置的圆台的俯视图是一个圆
2.将长方体截去一个四棱锥,得到的几何体如下图所示,则该几何体的左视图为(
).
3.一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是(
)
(A)球
(B)三棱锥
(C)正方体
(D)圆柱
4.如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为________.
如图,是由六个小正方体组合而成的一个立体图形,它的主视图是(
)。
6.
从上面俯视图中所示的两个物体,看到的是()。
7.
将如图的直角三角形绕直角边旋转一周,所得几何体从正面看是()。
三、解答题(每小题15分,60分)
1.
如图所示是一个直四棱柱及其正视图和俯视图(等腰梯形).
(1)根据图中所给数据,可得俯视图(等腰梯形)的高为
;
(2)在虚线框内画出其左视图,并标出各边的长.(尺规作图,不写作法,保留作图痕迹)
2.
已知物体三视图的外轮廓,如何构思该物体?
3.用小方块搭一个几何体,使得它的主视图和俯视图如图所示,这样的几何体只有一种吗
4、一几何体按比例绘制的三视图如图所示(单位:m):
(1)试画出它的直观图;
(2)求它的表面积和体积.
参考答案
选择题
A
【解析】画几何体的三视图要考虑视角,但对于球无论选择怎样的视角,其三视图总是三个全等的圆.答案A
2.
D
【解析】被截去的四棱锥的三条可见侧棱中有两条为长方体的面对角线,它们在右侧面上的投影与右侧面(长方形)的两条边重合,另一条为体对角线,它在右侧面上的投影与右侧面的对角线重合,对照各图,只有选项D符合.答案:D
3. D
【解析】一般地,圆柱的正视图是矩形,侧视图是矩形,而俯视图是圆.而球、正方体、三棱锥的三视图形状都相同,大小均相等是可以的,故选D.
4.
2
【解析】(构造法)由主视图和俯视图可知几何体是正方体切割后的一部分(四棱锥C1-
ABCD),还原在正方体中,如图所示.多面体最长的一条棱即为正方体的体对角线,如图即AC1.由正方体棱长AB=2知最长棱AC1的长为2.答案是2
【点评】
构造正方体,本题就很容易得出结论,此种方法在立体几何问题中较为常见,把抽象问题转化为直观问题解决.
B
【解析】主视图是在正面从前向后观察物体得到的图形。从前向后观察物体得到的图形含有三列两行,从左到右每列的正方形的个数是2、2、1,从下到上的每行的正方形的个数是3、2。
故本题正确答案为B。
A
【解析】由于正方体的俯视图是个正方形,而竖着的圆柱体的俯视图是个圆形,因此只有A的图形符合这个条件。故选A.
D
【解析】先根据旋转的性质可得直角三角形ABC绕直角边AC旋转一周可得到的几何体为圆锥,再根据圆锥的正视图即可作出判断。
∵直角三角形ABC绕直角边AC旋转一周得到的几何体为圆锥
∴所得几何体从正面看是等腰三角形
故选D.
二、解答题
1.
解:(1)
4
(2)
2.
3.
4.
(1)直观图如图所示.
(2)由三视图可知该几何体是长方体被截去一个角,且该几何体的体积是以A1A,A1D1,A1B1为棱的长方体的体积的34,
在直角梯形AA1B1B中,作BE⊥A1B1于E,
则四边形AA1EB是正方形,
∴AA1=BE=1,
在Rt△BEB1中,BE=1,EB1=1,
∴BB1=2,
∴几何体的表面积
S=S正方形ABCD+S矩形A1B1C1D1+2S梯形AA1B1B+S矩形BB1C1C+S正方形AA1D1D
=1+2×1+2×12×(1+2)×1+1×2+1=7+2(m2).
∴几何体的体积V=34×1×2×1=32(m3),
∴该几何体的表面积为(7+2)
m2,体积为32
m3.
