3.2中位数和众数 课件

课件29张PPT。中位数与众数 招聘启事
本公司需要招聘技术员一人, 有意者请来公司面试。
本山公司人事部
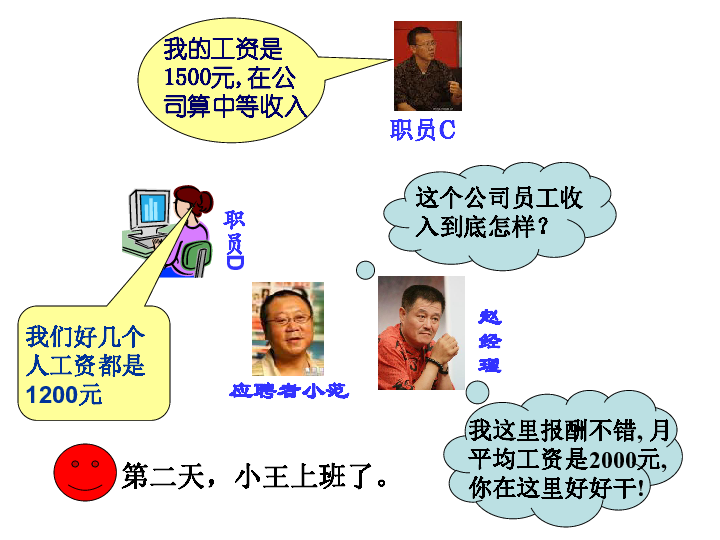
2016年10月18日赵经理应聘者小范第二天，小王上班了。职员C职员D小范在公司工作了一周后下表是该公司月工资报表:请大家仔细观察表中的数据,讨论该公司员
工的月平均工资是多少? 经理是否欺骗了小范?月平均工资是指：所有员工工资的平均数。下表是该公司月工资报表:平均月工资能否客观地反映员工的实际收入?(3) 你认为用什么数据反映一般技术员的实际收入比较合适，请说明理由。中位数定义：众数的定义： 在一组数据中，出现次数最多的数据叫做这组数据的众数。如上表中的1200 将一组数据按从大到小依次排列，把处在最中间位置的一个
数据叫做这组数据的中位数。 职员C职员D中位数定义： 将一组数据按大小依次排列，把处在最中间位置的一个
数据（当为偶数个数据时，为最中间两个数的平均数）
叫做这组数据的中位数。 如上表中，中位数为（1500+1200）/2=1350一个月后公司根据技术水平及表现，对其工资进行调整。15001500（1）此时的中位数是多少？5000，4000，1800，1500，1500，1500，1200，1200，1200，4001500（2）此时的众数是多少？当两个数据出现的次数并列最多，我就说这两个数都是众数。1200和1500所以一组数据的众数是不唯一的，可以有不止一个众数。求中位数要注意数据的大小排序 合作讨论：请你构造两组数据，一组有不止一个众数，一组没有众数2，2，3，3，3，4，4，41，2，3，4，5，6做一做：（1）在一组数据1、0、4、5、8中插入一个数据x，使该组数据的中位数为3，则x=_______（2）数据2、4、5、3、9、4、1、8的众数是_____，中位数是______，平均数为______2444.4（3）数据5、4、5、6、4、7、9的众数是_____4和5议一议：通过这个练习你能说说中位数和众数的特性吗？202021320205练一练20和3521201.一组数据的平均数一定只有一个x√ 2.一组数据的中位数一定只有一个√ 4.一组数据的众数一定只有一个5.一组数据的平均数，中位数，众数可以是同一个数3.一组数据的中位数一定是这组数据中的某个数。x√ 1，2，3，4，51，2，3，4，5，6由上知中位数3.51，1，1，1，1辨一辨典型例题公园里甲、乙两群游客正在做团体游戏，两群游客的年龄如下：(单位岁）
甲群：13，13，14，15，15，15，15，16，17，17
乙群：54，3，4，4，5，5，6，6，6，57（1）甲群游客年龄的平均数、中位数、众数各是多少岁？其中哪个统计量能较好的反映甲群游客的年龄特征。中位数是15，众数是15所以平均数、中位数、众数都能反映甲群游客的年龄特征。典型例题公园里甲、乙两群游客正在做团体游戏，两群游客的年龄如下：(单位岁）
甲群：13，13，14，15，15，15，15，16，17，17
乙群：54，3，4，4，5，5，6，6，6，57（2）乙群游客年龄的平均数、中位数、众数各是多少岁？其中哪个统计量能较好的反映甲群游客的年龄特征。中位数是5.5，众数是6排序后3，4，4，5，5，6，6，6，54，57课内练习：1、某风景区在“五一”黄金周期间，每天接待的旅游人数统计如下：表中表示人数这组数据中，
众数和中位数分别是（ ）22做一做： 甲、乙两班同学举行电脑汉字输入速度比赛，各派10名选手参加，参赛选手每分输入汉字个数统计如下：（1）分别求出各班选手每分输入汉字个数的平均数、 中位数和众数，并填入上表。（2）根据（1）中的结果，对两班选手的汉字输入 速度作简短评论。135135135134134.5135注意：1.一组数据中的众数有时不只一个，如数据2、3、－1、2、1、3中，2和3都出现了2次，它们都是这组数据的众数。2．当数据个数为奇数时，中位数是这组数据中的一个数据；但当数据个数为偶数时，其中位数是最中间两个数据的平均数，它不一定与这组数据中的某个数据相等。 八年级某班的教室内，三位同学正在为谁的数学成绩最好而争论，他们的5次数学成绩分别是:
他们都认为自己的成绩比另外两位同学好,请问他们分别从哪一方面来说的?从三人的测验对照图来看,你认为哪一个同学的成绩最好呢? 试一试：3、该厂生产销售了一批女鞋３０双，其中各种尺码的销售量如下表所示：1）.计算30双女鞋尺寸的平均数、中位数、众数2）.从实际出发，请回答1中三种统计特征量
对指导本厂的生产是否有实际意义？ 平均数、众数及中位数都是描述一组数据的集中趋势的特征数，但描述的角度和适用范围有所不同。
平均数的大小与一组数据里的每个数据均有关系，其中任何数据的变动都会相应引起平均数的变动；计算平均数的时候，所有的数据都参加运算，它能充分利用数据所提供的信息，在现实生活中较为常用；但它容易受到极端值的影响。
众数着眼于对各数据出现的频数的考察，其大小只与这组数据中的部分数据有关。当一组数据中有不少数据多次重复出现时，其众数往往是我们关心的一种统计量；但各个数据的重复次数大致相等时，众数往往没有特别意义。 平均数、众数及中位数都是描述一组数据的集中趋势的特征数，但描述的角度和适用范围有所不同。
中位数则仅与数据的排列位置有关，某些数据的变动对它的中位数没有影响。当一组数据中的个别数据变动较大时，可用它来描述其集中趋势。
中位数的优点计算简单，受极端值的影响较小，但不能充分利用所有数据的信息。 补充练习1
1、已知一组数据10，10，x,8(由大到小排列)的中位数与平均数相等，求x值及这组数据的中位数。 解：∵10，10，x,8的中位数与平均数相等
∴ (10+x)/2＝ (10+10+x+8)/4 ∴x＝8,
(10+x)/2＝9 ∴这组数据中的中位数是9。2、当5个整数从小到大排列，其中位数是4，如果这个数集的唯一众数是6，则这5个整数可能的最大的和是( )。
A.21 B.22 C.23 D.24。A3、某商场在一个月内销售某中品牌的冰箱共58台，具体情况如下：?
请问此商场的经理关注的是这组数据的平均数吗？他关注的是什么？为什么？如果你是经理，你将如何调整这种冰箱的进货数量呢？做一做： 1、有人对展览馆七天中每天进馆参观的人数做了记录，情况如下：
180，176，176，173，176，181，182
求这组数据的中位数和众数。2、下面数据的平均数、中位数和众数各是多少？
8，10，10，13，13，13，14，15，17，18，注意:2、众数是一组数据中出现次数最多的数据，是一组数据中的原数据，而不是相应的次数． 1、求中位数要将一组数据按大小顺序，而不必计算，顾名思义，中位数就是位置处于最中间的一个数（或最中间的两个数的平均数），排序时，从小到大或从大到小都可以． 谈谈学习本节课有什么体会与收获？
学习本节课内容后，你在今后的生活中对待一 些事情进行分析时，对你会有什么帮助？
小结：作业：（1）P84作业题 1、2、3、4
（2）作业本
谢谢！