《3.7正多边形》同步练习（附答案）

3.7__正多边形__
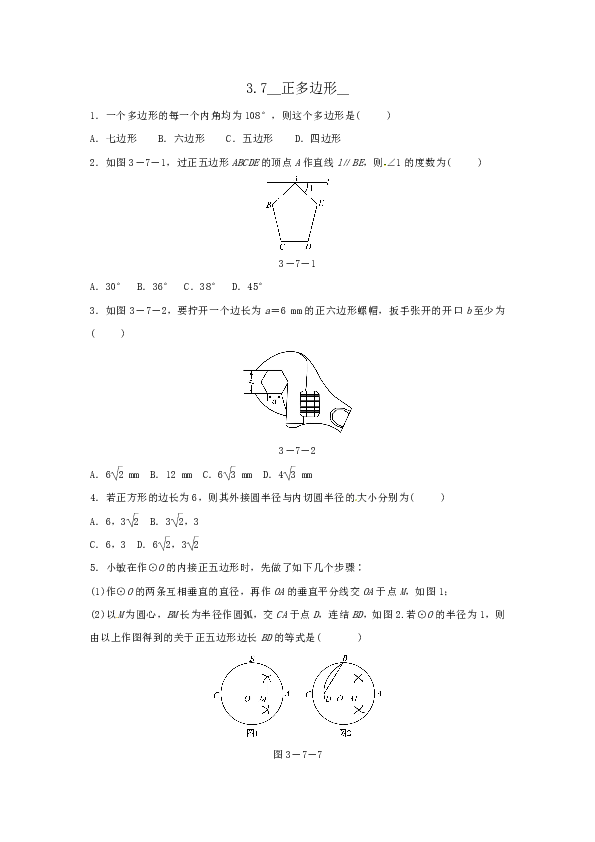
1．一个多边形的每一个内角均为108°，则这个多边形是(　
　)
A．七边形　　B．六边形　　C．五边形　　D．四边形
2．如图3－7－1，过正五边形ABCDE的顶点A作直线l∥BE，则∠1的度数为(　
　)
3－7－1
A．30°
B．36°
C．38°
D．45°
3．如图3－7－2，要拧开一个边长为a＝6
mm的正六边形螺帽，扳手张开的开口b至少为(　
　)
3－7－2
A．6
mm
B．12
mm
C．6
mm
D．4
mm
4．若正方形的边长为6，则其外接圆半径与内切圆半径的大小分别为(　
　)
A．6，3
B．3，3
C．6，3
D．6，3
5．小敏在作⊙O的内接正五边形时，先做了如下几个步骤∶
(1)作⊙O的两条互相垂直的直径，再作OA的垂直平分线交OA于点M，如图1；
(2)以M为圆心，BM长为半径作圆弧，交CA于点D，连结BD，如图2.若⊙O的半径为1，则由以上作图得到的关于正五边形边长BD的等式是(　
　)
图3－7－7
A．BD2＝OD
B．BD2＝OD
C．BD2＝OD
D．BD2＝OD
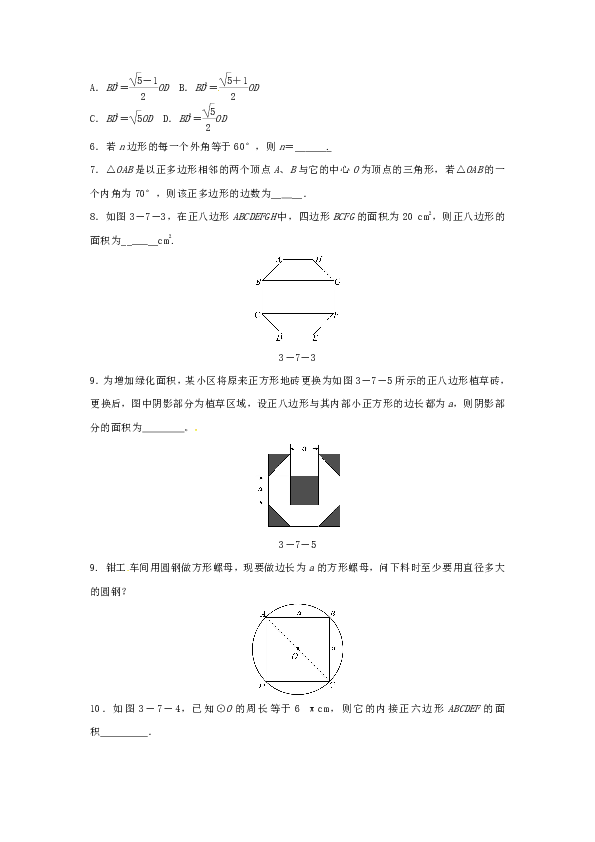
6．若n边形的每一个外角等于60°，则n＝__
_.
7．△OAB是以正多边形相邻的两个顶点A、B与它的中心O为顶点的三角形，若△OAB的一个内角为70°，则该正多边形的边数为__
__．
8．如图3－7－3，在正八边形ABCDEFGH中，四边形BCFG的面积为20
cm2，则正八边形的面积为__
__cm2.
3－7－3
9．为增加绿化面积，某小区将原来正方形地砖更换为如图3－7－5所示的正八边形植草砖，更换后，图中阴影部分为植草区域，设正八边形与其内部小正方形的边长都为a，则阴影部分的面积为
。
3－7－5
9.
钳工车间用圆钢做方形螺母，现要做边长为a的方形螺母，问下料时至少要用直径多大的圆钢？
10．如图3－7－4，已知⊙O的周长等于6
πcm，则它的内接正六边形ABCDEF的面积
．
3－7－4
第10题答图
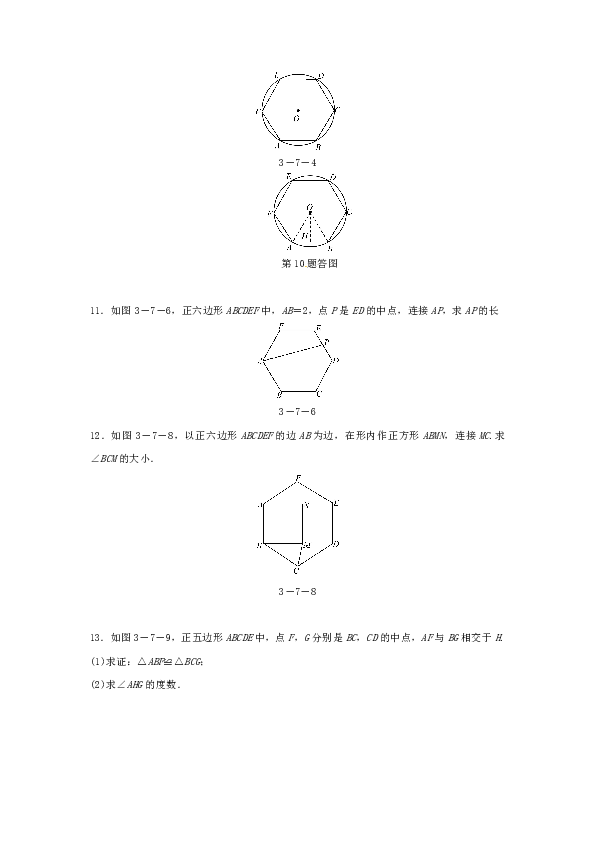
11．如图3－7－6，正六边形ABCDEF中，AB＝2，点P是ED的中点，连接AP，求AP的长
3－7－6
12．如图3－7－8，以正六边形ABCDEF的边AB为边，在形内作正方形ABMN，连接MC.求∠BCM的大小．
3－7－8
13．如图3－7－9，正五边形ABCDE中，点F，G分别是BC，CD的中点，AF与BG相交于H.
(1)求证：△ABF≌△BCG；
(2)求∠AHG的度数．
3－7－9
3.7__正多边形__
1．
C
2．
B
3．
C
4．
B
5．
C
6．
__6__.
7．
__9__．
8．
_40__cm2.
9．
2a2
10．
第10题答图
解：过点O作OH⊥AB于点H，连接OA，OB，
∴AH＝AB，
∵⊙O的周长等于6
πcm，∴⊙O的半径为3
cm，
∵∠AOB＝×360°＝60°，
∵OA＝OB，∴△OAB是等边三角形，
∴AB＝OA＝3
cm，∴所求面积为.
11．
　　　
第11题答图
【解析】如图，连接AE，在正六边形中，∠F＝×(6－2)·180°＝120°，
∵AF＝EF，
∴∠AEF＝∠EAF＝(180°－120°)＝30°，
∴∠AEP＝120°－30°＝90°，
∵点P是ED的中点，
∴EP＝×2＝1，
在Rt△AEP中，AP＝＝＝.
12．
解：∵六边形ABCDEF为正六边形，
∴∠ABC＝120°，AB＝BC.
∵四边形ABMN为正方形，
∴∠ABM＝90°，AB＝BM.∴∠MBC＝120°－90°＝30°，BM＝BC.
∴∠BCM＝∠BMC.
∴∠BCM＝×(180°－30°)＝75°.
13．解：(1)证明：∵五边形ABCDE是正五边形，
∴AB＝BC＝CD，∠ABC＝∠BCD，∴F，G分别是BC，CD的中点，
∴BF＝CG，在△ABF和BCG中，
AB＝BC，∠ABC＝∠BCD，BF＝CG，∴△ABF≌△BCG；
(2)由(1)知∠GBC＝∠FAB，
∵∠AHG＝∠FAB＋∠ABH＝∠GBC＋∠ABH＝∠ABC，
∵正五边形的内角为108°，
∴∠AHG＝108°.