4.1多边形同步练习（1）

浙教版八下数学4.1多边形同步练习（1）
　
一．选择题（共7小题）
1．下列图形不具有稳定性的是（　　）
A． B． C． D．
2．把一张形状是多边形的纸片剪去其中某一个角，剩下的部分是一个四边形，则这张纸片原来的形状不可能是（　　）21·世纪*教育网
A．六边形 B．五边形 C．四边形 D．三角形
3．在四边形ABCD中，若∠A+∠B+∠C=260°，则∠D的度数为（　　）
A．120° B．110° C．100° D．40°
4．从五边形的一个顶点出发，分别连接这个点与其余各顶点，可以把五边形分割成几个三角形（　　）
A．2个 B．3个 C．4个 D．5个
5．如图，在四边形ABCD中，∠A=65°，∠D=105°，∠B的外角是70°，则∠C等于（　　）
A．110° B．90° C．80° D．70°
6．以线段a=7，b=8，c=9，d=11为边作四边形，可作（　　）
A．一个 B．2个 C．3个 D．无数个
7．如图，已知O是四边形ABCD内一点，OA=OB=OC，∠ABC=∠ADC=70°，则∠DAO+∠DCO的大小是（　　）21教育网
A．70° B．110° C．140° D．150°
二．填空题（共5小题）
8．如图，已知正五边形ABCDE，AF∥CD，交DB的延长线于点F，则∠DFA=　　度．

8题 9题 11题 12题
9．某花园内有一块五边形的空地如图所示，为了美化环境，现计划在五边形各顶点为圆心，2m长为半径的扇形区域（阴影部分）种上花草，那么种上花草的扇形区域总面积是　　．www-2-1-cnjy-com
10．若从一个多边形的一个顶点出发，最多可以引10条对角线，则它是　　边形．
11．如图，已知五边形ABCDE中，AB∥ED，∠A=∠B=90°，则可以将该五边形ABCDE分成面积相等的两部分的直线有　　条．2-1-c-n-j-y
12．如图，在正六边形ABCDEF内放入2008个点，若这2008个点连同正六边形的六个顶点无三点共线，则该正六边形被这些点分成互不重合的三角形共　　个．21*cnjy*com　
三．解答题（共9小题）
13．在四边形ABCD中，∠B，∠C的外角分别是80°，92°，并且∠A比∠D大11°，求此四边形各内角的度数．【来源：21cnj*y.co*m】
14．在四边形ABCD中，∠A：∠B：∠C：∠D=2：4：1：5
（1）求四边形ABCD的四个内角的度数；
（2）四边形ABCD中是否有互相平行的边？若有，指出来；若没有，请说明理由．
15．如图，在四边形ABCD中，∠B+∠D=180°，∠DCE是四边形ABCD的一个外角，∠DCE与∠A相等吗？为什么？【出处：21教育名师】
16．如图，在四边形ABCD中，∠A=∠C=90°．
（1）求证：∠ABC+∠ADC=180°；
（2）作∠ABC的平分线BE交AD于点E，作DF∥BE于点F，求证：DF平分∠ADC．
17．如图，在四边形ABCD中，∠A=∠B，∠C=∠ADC
（1）求证：AB∥CD；
（2）过点D作DE∥BC交AB于点E，若∠ADC﹣∠A=60°，请判断△ADE是哪种特殊的三角形，并说明理由．【版权所有：21教育】
如图，四边形ABCD中，AB⊥BC，∠A+∠B=160°，∠D=4∠C，求四边形ABCD各内角的度数．21教育名师原创作品
19．如图，求∠A+∠B+∠C+∠D+∠E+∠F 的度数（提示：构造四边形，利用多边形内角和求解）
20．（1）我们知道三角形的内角和是180°，请猜测四边形的内角和是多少度？
解：四边形的四个内角和等于　　°
（2）利用下面两种方法验证你的猜想，请说明理由：
解法一：如图1，连接四边形ABCD的对角线AC．
解法二：如图2，延长CB、DA相交于点E．
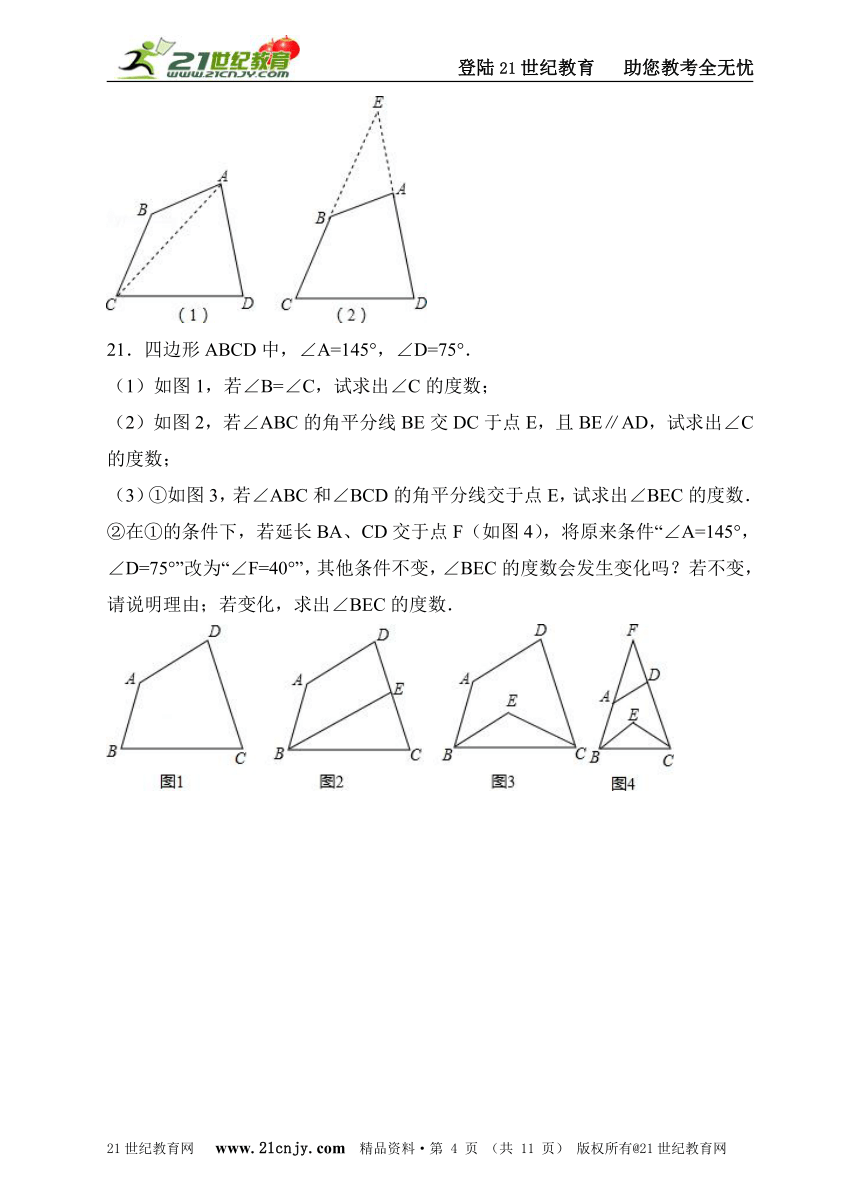
21．四边形ABCD中，∠A=145°，∠D=75°．
（1）如图1，若∠B=∠C，试求出∠C的度数；
（2）如图2，若∠ABC的角平分线BE交DC于点E，且BE∥AD，试求出∠C的度数；
（3）①如图3，若∠ABC和∠BCD的角平分线交于点E，试求出∠BEC的度数．
②在①的条件下，若延长BA、CD交于点F（如图4），将原来条件“∠A=145°，∠D=75°”改为“∠F=40°”，其他条件不变，∠BEC的度数会发生变化吗？若不变，请说明理由；若变化，求出∠BEC的度数．www.21-cn-jy.com
　
浙教版八下数学4.1多边形同步练习（1）
参考答案与试题解析
　
一．选择题（共7小题）
1．解：根据三角形的稳定性可得，B、C、D都具有稳定性．不具有稳定性的是A选项．故选A．
　
2．解：当剪去一个角后，剩下的部分是一个四边形，
则这张纸片原来的形状可能是四边形或三角形或五边形，不可能是六边形．
故选：A．
　
3．解：∵在四边形ABCD中，∠A+∠B+∠C+∠D=360°，且∠A+∠B+∠C=260°，
∴∠D=100°，
故选C
　
4．解：当n=5时，则有5﹣2=3个．
故选B．
　
5．解：∵∠B的外角是70°，
∴∠ABC=110°，
∵在四边形ABCD中，∠A=65°，∠D=105°，
∴∠C=360°﹣∠A﹣∠D﹣∠C=360°﹣65°﹣105°﹣110°=80°，
故选：C．
　
6．解：四条线段组成的四边形可有无数种变化．
故选D．
　
7．解：根据四边形的内角和定理可得：
∠DAB+∠DCB=220°，
∵OA=OB=OC，∠ABC=∠ADC=70°，
∴∠OAB=∠OBA，∠OCB=∠OBC，
∴∠OAB+∠OCB=70°，
∴∠DAO+∠DCO=220°﹣70°=150度．
故选D．
　
二．填空题（共5小题）
8．解：∵正五边形的外角为360°÷5=72°，
∴∠C=180°﹣72°=108°，
∵CD=CB，
∴∠CDB=36°，
∵AF∥CD，
∴∠DFA=∠CDB=36°，
故答案为：36．
　
9．解：∵五边形的内角和=（5﹣2）×180°=540°，
∴五个扇形的面积和==6π，
∴种上花草的扇形区域总面积6πm2．
故答案为6πm2．
　
10．解：设这个多边形是n边形．
依题意，得n﹣3=10，
∴n=13．
故这个多边形是13边形．
　
11．解：将该五边形ABCDE分成面积相等的两部分的直线有无数条．
　
12．解：∵正六边形ABCDEF内放入2008个点，这2008个点连同正六边形的六个顶点无三点共线，21世纪教育网版权所有
∴共有2008+6=2014个点．
∵在正六边形内放入1个点时，该正六边形被这个点分成互不重合的三角形共6个；即当n=1时，有6个；然后出现第2个点时，这个点必然存在于开始的6个中的某一个三角形内，然后此点将那个三角形又分成3个三角形，三角形数量便增加2个；又出现第3个点时，同理，必然出现在某个已存在的三角形内，然后又将此三角形1分为3，增加2个…，21cnjy.com
∴内部的点每增加1个，三角形个数便增加2个．
于是我们得到一个等差数列：存在n个点时，三角形数目an=a1+（n﹣1）d=6+2（n﹣1）=2n+4（n≥1）．21·cn·jy·com
由题干知，2008个点的总数为a2008=2×2008+4=4020（个）．
　
三．解答题（共9小题）
13．解：∵∠B，∠C的外角分别是80°，92°，
∴∠B=100°，∠C=88°，
∴∠A+∠D=360°﹣100°﹣88°=172°，
∵∠A比∠D大11°，
∴∠A=91.5°，∠D=80.5°．
　
14．解：（1）∵在四边形ABCD中，∠A：∠B：∠C：∠D=2：4：1：5，
∴设∠A=2x，∠B=4x，∠C=x，∠D=5x，
∵∠A+∠B+∠C+∠D=360°，
∴2x+4x+x+5x=360°，
解得：x=30°，
∴∠A=60°，∠B=120°，∠C=30，∠D=150°；
（2）四边形ABCD中有互相平行的边，
∵∠A+∠B=180°，
∴AD∥BC．
　
15．解：∵在四边形ABCD中内角和为360°，
∴∠A+∠B+∠BCD+∠D=360°，
又∵∠B+∠D=180°，
∴∠A+∠BCD=180°，
又∵∠DCE+∠BCD=180°，
∴∠DCE=∠A．
　
16．证明：（1）∵四边形ABCD中，∠A+∠ABC+∠C+∠ADC=360°，∠A=∠C=90°，2·1·c·n·j·y
∴∠ABC+∠ADC=180°，
（2）∵DF∥BE，
∴∠2=∠DFC，
∵∠1=∠2，直角△DCF中，∠DFC+∠4=90°，
∴∠ABC+∠4=90°，
∵∠ABC+∠ADC=180°，
即∠ABC+∠ADC=90°，
∴∠ADC=∠4，
∴∠3=∠4，即DF平分∠ADC．
　
17．（1）证明：∵四边形ABCD中，∠A=∠B，∠C=∠ADC，
∴∠A+∠B+∠C+∠ADC=2∠A+2∠ADC=360°，
∴∠A+∠ADC=180°，
∴AB∥DC；
（2）是等边三角形，
理由是：∵∠A+∠ADC=180°，∠ADC﹣∠A=60°，
∴∠A=60°，
∵∠B=∠A，
∴∠B=60°，
∵DE∥BC，
∴∠DEA=∠B=60°，
∴AD=DE，
∴△ADE是等边三角形（有一个角是60°的等腰三角形是等边三角形）．
　
18．解：∵AB⊥BC，
∴∠B=90°，
∵∠A+∠B=160°，
∴∠A=70°，
∵∠A+∠B+∠C+∠D=360°，
∴∠C+∠D=200°，
∵∠D=4∠C，
∴∠C=40°，
∴∠D=160°．
　
19．解：如图，连接AD．
∵∠1=∠E+∠F，∠1=∠ADE+∠DAF，
∴∠E+∠F=∠ADE+∠DAF，
∴∠BAD+∠B+∠C+∠CDA=360°，
∴∠BAF+∠B+∠C+∠CDE+∠E+∠F=360°．
故∠A+∠B+∠C+∠D+∠E+∠F的度数是360°．
　
20．解：（1）360°；
故答案为：360．
（2）证明：解法一：连接AC，
∵∠B+∠BAC+∠BCA=180°，∠D+∠DAC+∠DCA=180°，
∴∠BAD+∠B+∠BCD+∠D=∠B+∠BAC+∠BCA+∠D+∠DAC+∠DCA=360°，
∴四边形的四个内角和等于360°；
解法二：延长CB、DA相交于点E，
∵∠E+∠C+∠D=180°，∠E+∠EBA+∠EAB=180°，
∴∠C+∠D=180°﹣∠E，∠EBA+∠EAB=180°﹣∠E，
∵∠CBA+∠EBA=180°，∠DAB+∠EAB=180°，
∴∠ABC+∠DAB=180°﹣∠EBA+180°﹣∠EAB=360°﹣（∠EBA+∠EAB）=360°﹣（180°﹣∠E）=180°+∠E，【来源：21·世纪·教育·网】
∴∠DAB+∠ABC+∠C+∠D=180°+∠E+180°﹣∠E=360°．
∴四边形的四个内角和等于360°．
　
21．解：（1）∵四边形ABCD中，∠A=145°，∠D=75°，
∴∠B+∠C=360°﹣（145°+75°）=140°，
∵∠B=∠C，
∴∠C=70°；
（2）∵BE∥AD，
∴∠ABE=180°﹣∠A=180°﹣145°=35°，
∵∠ABC的角平分线BE交DC于点E，
∴∠ABC=70°，
∴∠C=360°﹣（145°+75°+70°）=70°；
（3）①∵四边形ABCD中，∠A=145°，∠D=75°，
∴∠B+∠C=360°﹣（145°+75°）=140°，
∵∠ABC和∠BCD的角平分线交于点E，
∴∠EBC+∠ECB=70°，
∴∠BEC=180°﹣70°=110°；
②不变．
∵∠F=40°，
∴∠FBC+∠BCF=180°﹣40°=140°，
∵∵∠ABC和∠BCD的角平分线交于点E，
∴∠EBC+∠ECB=70°，
∴∠BEC=180°﹣70°=110°．