4.2平行四边形及其性质同步练习(1)
文档属性
| 名称 | 4.2平行四边形及其性质同步练习(1) |

|
|
| 格式 | zip | ||
| 文件大小 | 111.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-03-31 00:00:00 | ||
图片预览



文档简介
浙教版八下数学4.2平行四边形及其性质同步练习(1)
一.选择题(共9小题)
1.如图,在平行四边形ABCD中,EF∥AD,HN∥AB,则图中的平行四边形的个数共有( )
A.12个 B.9个 C.7个 D.5个
2.如图,将?ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为( )
A.66° B.104° C.114° D.124°
3.已知四边形ABCD是平行四边形,则下列各图中∠1与∠2一定不相等的是( )
A. B. C. D.
4.在平行四边形ABCD中,∠B=110°,延长AD至F,延长CD至E,连接EF,则∠E+∠F=( )21世纪教育网版权所有
A.110° B.30° C.50° D.70°
5.在?ABCD中,AB=3,BC=4,当?ABCD的面积最大时,下列结论正确的有( )
①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.
A.①②③ B.①②④ C.②③④ D.①③④
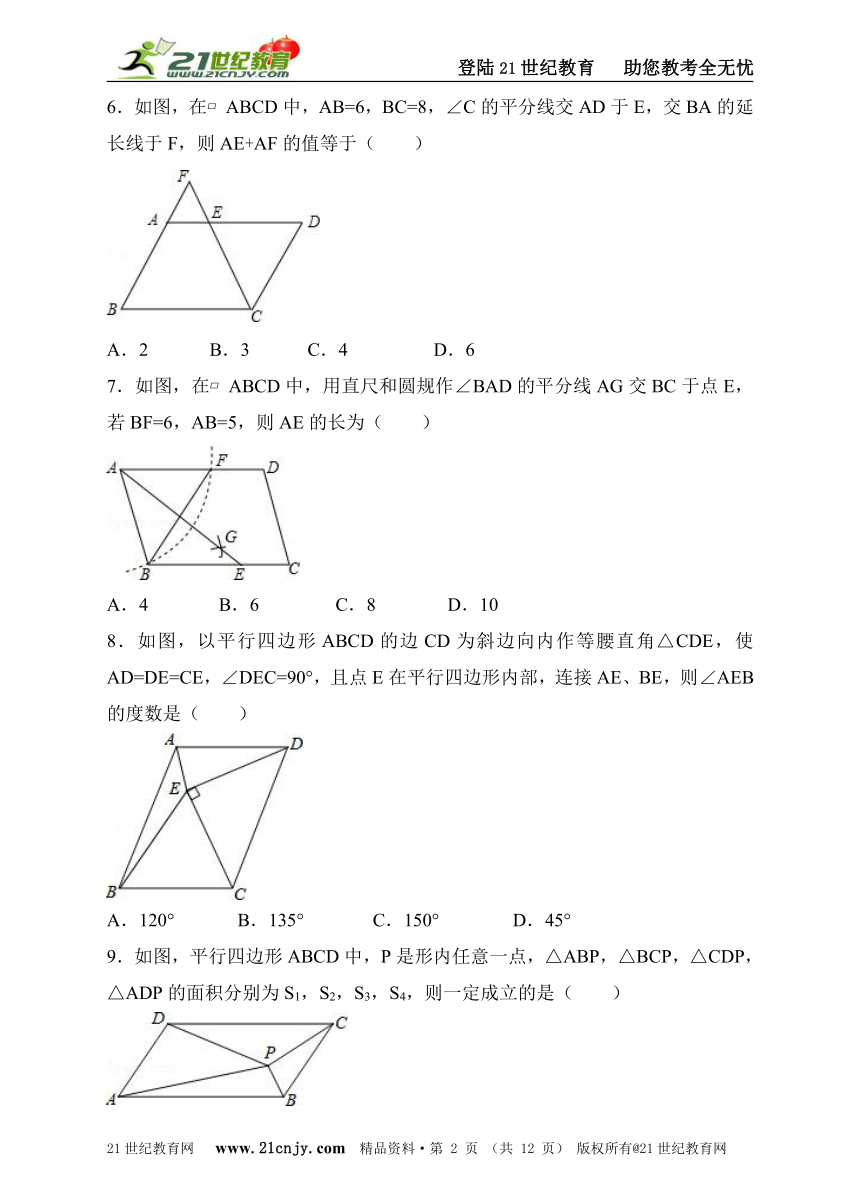
6.如图,在?ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于( )21教育网
A.2 B.3 C.4 D.6
7.如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( )21cnjy.com
A.4 B.6 C.8 D.10
8.如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是( )21·cn·jy·com
A.120° B.135° C.150° D.45°
9.如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )
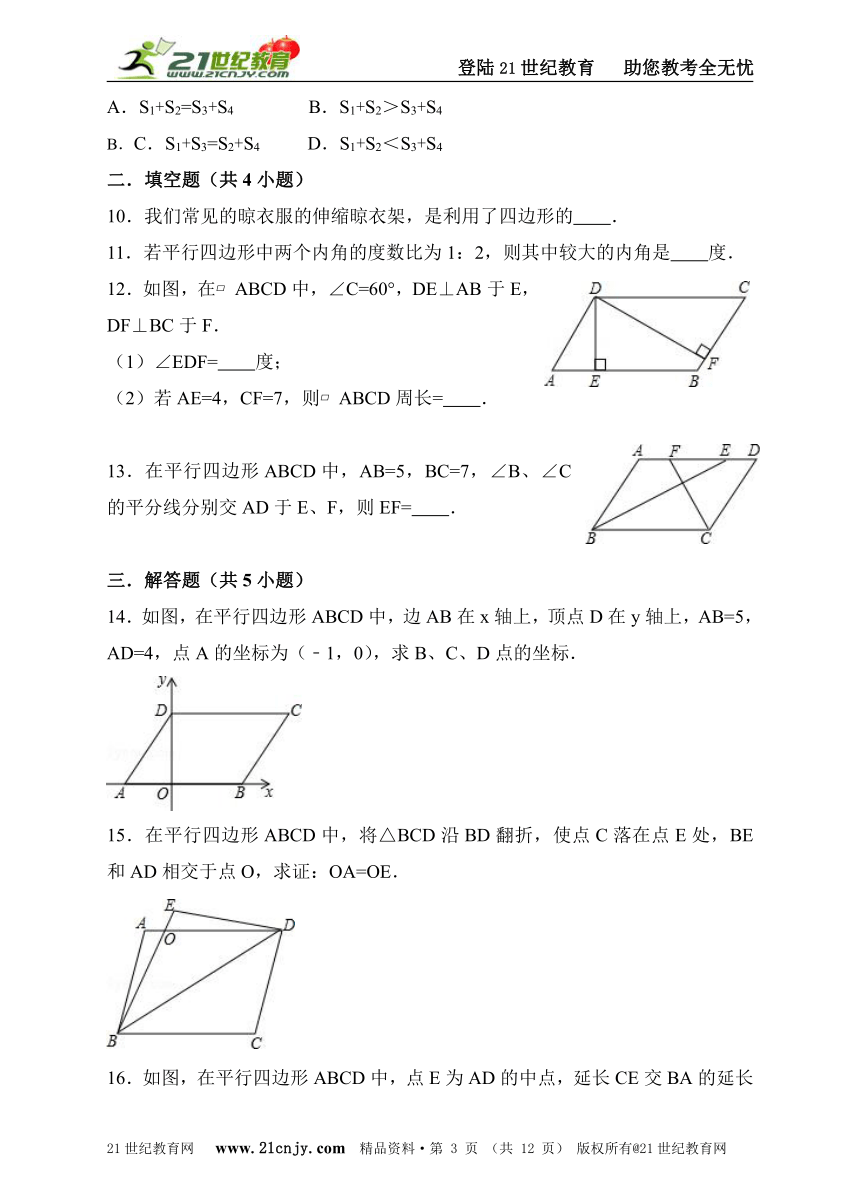
S1+S2=S3+S4 B.S1+S2>S3+S4
C.S1+S3=S2+S4 D.S1+S2<S3+S4
二.填空题(共4小题)
10.我们常见的晾衣服的伸缩晾衣架,是利用了四边形的 .
11.若平行四边形中两个内角的度数比为1:2,则其中较大的内角是 度.
12.如图,在?ABCD中,∠C=60°,DE⊥AB于E,DF⊥BC于F.
(1)∠EDF= 度;
(2)若AE=4,CF=7,则?ABCD周长= .
13.在平行四边形ABCD中,AB=5,BC=7,∠B、∠C的平分线分别交AD于E、F,则EF= .www.21-cn-jy.com
三.解答题(共5小题)
14.如图,在平行四边形ABCD中,边AB在x轴上,顶点D在y轴上,AB=5,AD=4,点A的坐标为(﹣1,0),求B、C、D点的坐标.2·1·c·n·j·y
15.在平行四边形ABCD中,将△BCD沿BD翻折,使点C落在点E处,BE和AD相交于点O,求证:OA=OE.【来源:21·世纪·教育·网】
16.如图,在平行四边形ABCD中,点E为AD的中点,延长CE交BA的延长线于点F.
(1)求证:AB=AF;
(2)若BC=2AB,∠BCD=110°,求∠ABE的度数.
17.已知:如图,在?ABCD中,AB=CD,AD=BC,AB∥CD,AB∥CD,点F在AB的延长线上,且BF=AB,联结FD交BC于点E.21·世纪*教育网
(1)证明:△DCE≌△FBE;
(2)若EC=3,求AD的长.
18.已知:如图,A为EF上一点,四边形ABCD是平行四边形且∠EAD=∠BAF.
(1)求证:△CEF是等腰三角形.
(2)△CEF的哪两边之和恰好等于平行四边形ABCD的周长?证明你的结论.
浙教版八下数学4.2平行四边形及其性质同步练习(1)
参考答案与试题解析
一.选择题(共9小题)
1.解:根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,则图中的四边AEOH,HOFD,EBNO,ONCF,AEFD,EBCF,ABNH,HNCD,ABCD都是平行四边形,共9个.www-2-1-cnjy-com
故选B.
2.解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ACD=∠BAC,
由折叠的性质得:∠BAC=∠B′AC,
∴∠BAC=∠ACD=∠B′AC=∠1=22°,
∴∠B=180°﹣∠2﹣∠BAC=180°﹣44°﹣22°=114°;
故选:C.
3.解:A正确;
∵∠1和∠2是对顶角,
∴∠1=∠2;
B、D正确;
∵四边形ABCD是平行四边形,
∴∠B=∠D,AB∥CD,
∴∠1=∠2;
C不正确;
故选:C.
4.解:∵四边形ABCD是平行四边形,
∴∠A=∠ADE=180°﹣∠B=70°
∵∠E+∠F=∠ADE
∴∠E+∠F=70°
故选D.
5.解:根据题意得:当?ABCD的面积最大时,四边形ABCD为矩形,
∴∠A=∠B=∠C=∠D=90°,AC=BD,
∴AC==5,
①正确,②正确,④正确;③不正确;
故选:B.
6.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BC=8,CD=AB=6,
∴∠F=∠DCF,
∵CF平分∠BCD,
∴∠FCB=∠DCF,
∴∠F=∠FCB,
∴BF=BC=8,
同理:DE=CD=6,
∴AF=BF﹣AB=2,AE=AD﹣DE=2,
∴AE+AF=4;
故选:C.
7.解:连结EF,AE与BF交于点O,如图
∵AB=AF,AO平分∠BAD,
∴AO⊥BF,BO=FO=BF=3,
∵四边形ABCD为平行四边形,
∴AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=EB,
而BO⊥AE,
∴AO=OE,
在Rt△AOB中,AO===4,
∴AE=2AO=8.
故选C.
8.解:∵四边形ABCD是平行四边形,
∴AD=BC,∠BAD=∠BCD,∠BAD+∠ADC=180°,
∵AD=DE=CE,
∴AD=DE=CE=BC,
∴∠DAE=∠AED,∠CBE=∠CEB,
∵∠DEC=90°,
∴∠EDC=∠ECD=45°,
设∠DAE=∠AED=x,∠CBE=∠CEB=y,
∴∠ADE=180°﹣2x,∠BCE=180°﹣2y,
∴∠ADC=180°﹣2x+45°=225°﹣2x,∠BCD=225°﹣2y,
∴∠BAD=180°﹣(225°﹣2x)=2x﹣45°,
∴2x﹣45°=225°﹣2y,
∴x+y=135°,
∴∠AEB=360°﹣135°﹣90°=135°;
故选:B.
9. 解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴S1+S3=平行四边形ABCD的面积,
S2+S4=平行四边形ABCD的面积,
∴S1+S3=S2+S4,
故选:C.
二.填空题(共4小题)
10.解:我们常见的晾衣服的伸缩晾衣架,是利用了四边形的灵活性,
故答案为:灵活性 或者不稳定性.
11.解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠B+∠C=180°,
∵∠B:∠C=1:2,
∴∠C=×180°=120°,
故答案为:120.
12.解:(1)∵四边形ABCD是平行四边形,
∴∠A=∠C=60°,∠A=180°﹣∠C=120°,
∵DE⊥AB,DF⊥BC,
∴∠DEB=∠DFB=90°,
∴∠EDF=360°﹣∠DEB﹣∠B﹣∠DFB=60°;
(2)∵∠A=∠C=60°,DE⊥AB,DF⊥BC,
∴∠ADE=∠CDF=30°,
∵AE=4,CF=7,
∴AD=2AE=8,CD=2CF=14,
∴AB=CD=14,BC=AD=8,
∴?ABCD周长为:AD+AB+BC+CD=44.
故答案为:(1)60°,(2)44.
13.解:∵BE平分∠ABC,
∴∠ABE=∠CBE,
又∵AD∥CB,
∴∠AEB=∠CBE,
∴∠ABE=∠AEB,
则AE=AB=5;
同理可得,DF=CD=5.
∴EF=AE+DF﹣AD=5+5﹣7=3.
故答案为:3.
三.解答题(共5小题)
14.解:∵在平行四边形ABCD中,AB=5,AD=4,点A的坐标为(﹣1,0),
∴AO=1,BO=5﹣1=4,DO==
故B(4,0),D(0,),
由平行四边形的性质得:AB=CD=5,故C(5,).
15.证明:平行四边形ABCD中,将△BCD沿BD对折,使点C落在E处,
可得∠DBE=∠ADB,∠A=∠C,
∴OB=OD,
在△AOB和△EOD中,
,
∴△AOB≌△EOD(AAS),
∴OA=OE.
16.(1)证明:∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AB,
∴∠DCE=∠F,∠FBC+∠BCD=180°,
∵E为AD的中点,
∴DE=AE.
在△DEC和△AEF中,
,
∴△DEC≌△AEF(AAS).
∴DC=AF.
∴AB=AF;
(2)解:由(1)可知BF=2AB,EF=EC,
∵∠BCD=110°,
∴∠FBC=180°﹣110°=70°,
∵BC=2AB,
∴BF=BC,
∴BE平分∠CBF,
∴∠ABE=∠FBC=×70°=35°.
17.(1)证明:∵AB∥CD,
∴∠FBE=∠C,
∵AB=DC,AB=BF,
∴BF=DC,
在△DCE和△FBE中,
,
∴△DCE≌△FBE(AAS);
(2)解:∵△DCE≌△FBE,
∴BE=EC=3,
∴AD=BC=6.
18.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥FC,AB∥EC,
∴∠FAB=∠E,∠EAD=∠F.
又∵∠EAD=∠BAF,
∴∠E=∠F.
∴△CEF是等腰三角形.
(2)结论:CE+CF=平行四边形ABCD的周长.
证明:由(1)可知:∠FAB=∠E,∠EAD=∠F,
∴∠F=∠BAF,∠DAE=∠E.
∴AB=BF,AD=DE,
∴?ABCD的周长=AB+BC+CD+AD=BF+BC+CD+DE=CE+CF.
一.选择题(共9小题)
1.如图,在平行四边形ABCD中,EF∥AD,HN∥AB,则图中的平行四边形的个数共有( )
A.12个 B.9个 C.7个 D.5个
2.如图,将?ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为( )
A.66° B.104° C.114° D.124°
3.已知四边形ABCD是平行四边形,则下列各图中∠1与∠2一定不相等的是( )
A. B. C. D.
4.在平行四边形ABCD中,∠B=110°,延长AD至F,延长CD至E,连接EF,则∠E+∠F=( )21世纪教育网版权所有
A.110° B.30° C.50° D.70°
5.在?ABCD中,AB=3,BC=4,当?ABCD的面积最大时,下列结论正确的有( )
①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.
A.①②③ B.①②④ C.②③④ D.①③④
6.如图,在?ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于( )21教育网
A.2 B.3 C.4 D.6
7.如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( )21cnjy.com
A.4 B.6 C.8 D.10
8.如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是( )21·cn·jy·com
A.120° B.135° C.150° D.45°
9.如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )
S1+S2=S3+S4 B.S1+S2>S3+S4
C.S1+S3=S2+S4 D.S1+S2<S3+S4
二.填空题(共4小题)
10.我们常见的晾衣服的伸缩晾衣架,是利用了四边形的 .
11.若平行四边形中两个内角的度数比为1:2,则其中较大的内角是 度.
12.如图,在?ABCD中,∠C=60°,DE⊥AB于E,DF⊥BC于F.
(1)∠EDF= 度;
(2)若AE=4,CF=7,则?ABCD周长= .
13.在平行四边形ABCD中,AB=5,BC=7,∠B、∠C的平分线分别交AD于E、F,则EF= .www.21-cn-jy.com
三.解答题(共5小题)
14.如图,在平行四边形ABCD中,边AB在x轴上,顶点D在y轴上,AB=5,AD=4,点A的坐标为(﹣1,0),求B、C、D点的坐标.2·1·c·n·j·y
15.在平行四边形ABCD中,将△BCD沿BD翻折,使点C落在点E处,BE和AD相交于点O,求证:OA=OE.【来源:21·世纪·教育·网】
16.如图,在平行四边形ABCD中,点E为AD的中点,延长CE交BA的延长线于点F.
(1)求证:AB=AF;
(2)若BC=2AB,∠BCD=110°,求∠ABE的度数.
17.已知:如图,在?ABCD中,AB=CD,AD=BC,AB∥CD,AB∥CD,点F在AB的延长线上,且BF=AB,联结FD交BC于点E.21·世纪*教育网
(1)证明:△DCE≌△FBE;
(2)若EC=3,求AD的长.
18.已知:如图,A为EF上一点,四边形ABCD是平行四边形且∠EAD=∠BAF.
(1)求证:△CEF是等腰三角形.
(2)△CEF的哪两边之和恰好等于平行四边形ABCD的周长?证明你的结论.
浙教版八下数学4.2平行四边形及其性质同步练习(1)
参考答案与试题解析
一.选择题(共9小题)
1.解:根据平行四边形的定义:两组对边分别平行的四边形是平行四边形,则图中的四边AEOH,HOFD,EBNO,ONCF,AEFD,EBCF,ABNH,HNCD,ABCD都是平行四边形,共9个.www-2-1-cnjy-com
故选B.
2.解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ACD=∠BAC,
由折叠的性质得:∠BAC=∠B′AC,
∴∠BAC=∠ACD=∠B′AC=∠1=22°,
∴∠B=180°﹣∠2﹣∠BAC=180°﹣44°﹣22°=114°;
故选:C.
3.解:A正确;
∵∠1和∠2是对顶角,
∴∠1=∠2;
B、D正确;
∵四边形ABCD是平行四边形,
∴∠B=∠D,AB∥CD,
∴∠1=∠2;
C不正确;
故选:C.
4.解:∵四边形ABCD是平行四边形,
∴∠A=∠ADE=180°﹣∠B=70°
∵∠E+∠F=∠ADE
∴∠E+∠F=70°
故选D.
5.解:根据题意得:当?ABCD的面积最大时,四边形ABCD为矩形,
∴∠A=∠B=∠C=∠D=90°,AC=BD,
∴AC==5,
①正确,②正确,④正确;③不正确;
故选:B.
6.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BC=8,CD=AB=6,
∴∠F=∠DCF,
∵CF平分∠BCD,
∴∠FCB=∠DCF,
∴∠F=∠FCB,
∴BF=BC=8,
同理:DE=CD=6,
∴AF=BF﹣AB=2,AE=AD﹣DE=2,
∴AE+AF=4;
故选:C.
7.解:连结EF,AE与BF交于点O,如图
∵AB=AF,AO平分∠BAD,
∴AO⊥BF,BO=FO=BF=3,
∵四边形ABCD为平行四边形,
∴AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=EB,
而BO⊥AE,
∴AO=OE,
在Rt△AOB中,AO===4,
∴AE=2AO=8.
故选C.
8.解:∵四边形ABCD是平行四边形,
∴AD=BC,∠BAD=∠BCD,∠BAD+∠ADC=180°,
∵AD=DE=CE,
∴AD=DE=CE=BC,
∴∠DAE=∠AED,∠CBE=∠CEB,
∵∠DEC=90°,
∴∠EDC=∠ECD=45°,
设∠DAE=∠AED=x,∠CBE=∠CEB=y,
∴∠ADE=180°﹣2x,∠BCE=180°﹣2y,
∴∠ADC=180°﹣2x+45°=225°﹣2x,∠BCD=225°﹣2y,
∴∠BAD=180°﹣(225°﹣2x)=2x﹣45°,
∴2x﹣45°=225°﹣2y,
∴x+y=135°,
∴∠AEB=360°﹣135°﹣90°=135°;
故选:B.
9. 解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴S1+S3=平行四边形ABCD的面积,
S2+S4=平行四边形ABCD的面积,
∴S1+S3=S2+S4,
故选:C.
二.填空题(共4小题)
10.解:我们常见的晾衣服的伸缩晾衣架,是利用了四边形的灵活性,
故答案为:灵活性 或者不稳定性.
11.解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠B+∠C=180°,
∵∠B:∠C=1:2,
∴∠C=×180°=120°,
故答案为:120.
12.解:(1)∵四边形ABCD是平行四边形,
∴∠A=∠C=60°,∠A=180°﹣∠C=120°,
∵DE⊥AB,DF⊥BC,
∴∠DEB=∠DFB=90°,
∴∠EDF=360°﹣∠DEB﹣∠B﹣∠DFB=60°;
(2)∵∠A=∠C=60°,DE⊥AB,DF⊥BC,
∴∠ADE=∠CDF=30°,
∵AE=4,CF=7,
∴AD=2AE=8,CD=2CF=14,
∴AB=CD=14,BC=AD=8,
∴?ABCD周长为:AD+AB+BC+CD=44.
故答案为:(1)60°,(2)44.
13.解:∵BE平分∠ABC,
∴∠ABE=∠CBE,
又∵AD∥CB,
∴∠AEB=∠CBE,
∴∠ABE=∠AEB,
则AE=AB=5;
同理可得,DF=CD=5.
∴EF=AE+DF﹣AD=5+5﹣7=3.
故答案为:3.
三.解答题(共5小题)
14.解:∵在平行四边形ABCD中,AB=5,AD=4,点A的坐标为(﹣1,0),
∴AO=1,BO=5﹣1=4,DO==
故B(4,0),D(0,),
由平行四边形的性质得:AB=CD=5,故C(5,).
15.证明:平行四边形ABCD中,将△BCD沿BD对折,使点C落在E处,
可得∠DBE=∠ADB,∠A=∠C,
∴OB=OD,
在△AOB和△EOD中,
,
∴△AOB≌△EOD(AAS),
∴OA=OE.
16.(1)证明:∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AB,
∴∠DCE=∠F,∠FBC+∠BCD=180°,
∵E为AD的中点,
∴DE=AE.
在△DEC和△AEF中,
,
∴△DEC≌△AEF(AAS).
∴DC=AF.
∴AB=AF;
(2)解:由(1)可知BF=2AB,EF=EC,
∵∠BCD=110°,
∴∠FBC=180°﹣110°=70°,
∵BC=2AB,
∴BF=BC,
∴BE平分∠CBF,
∴∠ABE=∠FBC=×70°=35°.
17.(1)证明:∵AB∥CD,
∴∠FBE=∠C,
∵AB=DC,AB=BF,
∴BF=DC,
在△DCE和△FBE中,
,
∴△DCE≌△FBE(AAS);
(2)解:∵△DCE≌△FBE,
∴BE=EC=3,
∴AD=BC=6.
18.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥FC,AB∥EC,
∴∠FAB=∠E,∠EAD=∠F.
又∵∠EAD=∠BAF,
∴∠E=∠F.
∴△CEF是等腰三角形.
(2)结论:CE+CF=平行四边形ABCD的周长.
证明:由(1)可知:∠FAB=∠E,∠EAD=∠F,
∴∠F=∠BAF,∠DAE=∠E.
∴AB=BF,AD=DE,
∴?ABCD的周长=AB+BC+CD+AD=BF+BC+CD+DE=CE+CF.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
