平行四边形及其性质 练习（基础题）

平行四边形及其性质
　
一．解答题（共6小题）
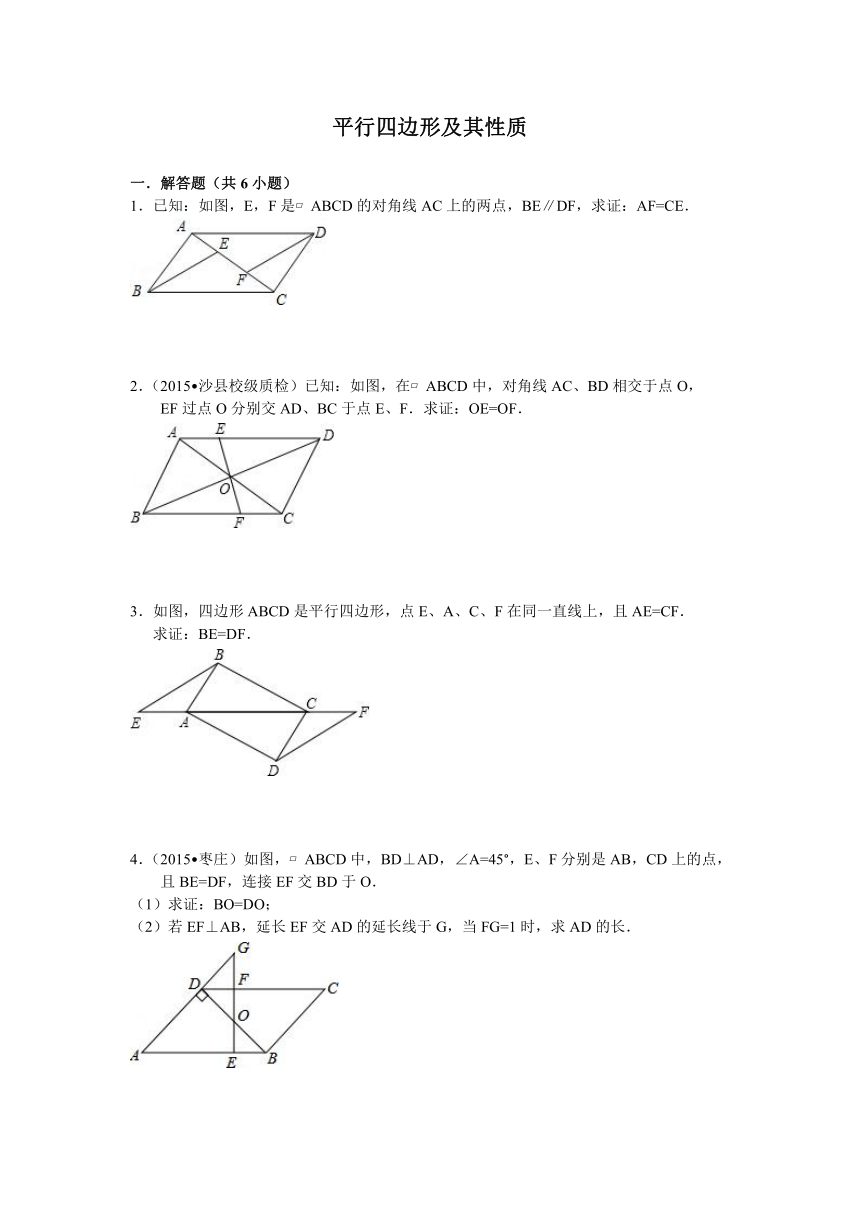
1．已知：如图，E，F是 ABCD的对角线AC上的两点，BE∥DF，求证：AF=CE．
( http: / / www.21cnjy.com )
　
2．（2015 沙县校级质检）已知：如图，在 ABCD中，对角线AC、BD相交于点O，
EF过点O分别交AD、BC于点E、F．求证：OE=OF．
( http: / / www.21cnjy.com )
　
3．如图，四边形ABCD是平行四边形，点E、A、C、F在同一直线上，且AE=CF．
求证：BE=DF．
( http: / / www.21cnjy.com )
　
4．（2015 枣庄）如图， ABCD中，BD⊥AD，∠A=45°，E、F分别是AB，CD上的点，且BE=DF，连接EF交BD于O．
（1）求证：BO=DO；
（2）若EF⊥AB，延长EF交AD的延长线于G，当FG=1时，求AD的长．
( http: / / www.21cnjy.com )
　
5．（2015 简阳市模拟）已知：如图，在平行四边形ABCD中，点M在边AD上，
且AM=DM．CM、BA的延长线相交于点E．求证：
（1）AE=AB；
（2）如果BM平分∠ABC，求证：BM⊥CE．
( http: / / www.21cnjy.com )
　
6．已知：如图，平行四边形ABCD中，AB=4，AD=6，∠A的平分线交BC于E，
交DC延长线于点F，BG⊥AE，垂足为G，射线BG交AD于H，交CD延长线于M
（1）求CE的长；
（2）求MF的长．
( http: / / www.21cnjy.com )
　
　
参考答案与试题解析
　
一．解答题（共6小题）
1．【解答】证明：在平行四边形ABCD中，
∵AD∥BC，AD=BC，∴∠ACB=∠CAD．又∵BE∥DF，∴∠BEC=∠DFA，
在△BEC与△DFA中，，∴△BEC≌△DFA，∴CE=AF．
　
2．【解答】证明：∵四边形ABCD是平行四边形，
∴AD∥BC，OA=OC．∴∠EAO=∠FCO，∠AEO=∠CFO，
在△AOE和△COF中，
，∴△AEO≌△CFO（AAS），∴OE=OF．
　
3．【解答】证明：∵四边形ABCD为平行四边形，
∴BC=AD，BC∥AD，∴∠BCA=∠DAC，
又∵AE=CF，∴EC=AF，在△BCE和△DAF中，
∴△BCE≌△DAF（SAS），∴BE=DF．
4．【解答】（1）证明：∵四边形ABCD是平行四边形，
∴DC=AB，DC∥AB，∴∠ODF=∠OBE，在△ODF与△OBE中
∴△ODF≌△OBE（AAS）∴BO=DO；
（2）解：∵BD⊥AD，∴∠ADB=90°，∵∠A=45°，∴∠DBA=∠A=45°，
∵EF⊥AB，∴∠G=∠A=45°，∴△ODG是等腰直角三角形，
∵AB∥CD，EF⊥AB，∴DF⊥OG，∴OF=FG，△DFG是等腰直角三角形，
∵△ODF≌△OBE（AAS）∴OE=OF，∴GF=OF=OE，即2FG=EF，
∵△DFG是等腰直角三角形，
∴DF=FG=1，∴DG==DO，
∴在等腰RT△ADB
中，DB=2DO=2=AD
∴AD=2，
　
5．【解答】证明：（1）∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD，∴∠E=∠DCM，在△AEM和△DCM中，
，∴△AEM≌△DCM（AAS），∴AE=CD，∴AE=AB；
（2）∵BM平分∠ABC，∴∠ABM=∠CBM，
∵四边形ABCD是平行四边形，∴AD∥BC，
∴∠CBM=∠AMB，∴∠ABM=∠AMB，∴AB=AM，
∵AB=AE，AM=DM，∴点M是AD的中点，∴BC=2AM，∴BC=BE，
∴△BCE是等腰三角形．
∵BM平分∠ABC，∴BM⊥CE．
6．【解答】解：（1）∵AE平分∠BAD，∴∠BAE=∠DAE，
∵四边形ABCD是平行四边形，∴AD∥BC，BC=AD=6，AB=CD=4，
∴∠DAE=∠AEB，∴∠BAE=∠AEB，∴BE=AB=4，∴CE=BC﹣BE=6﹣4=2；
（2）∵BG⊥AE，∴∠AGB=∠AGH，在△ABG和△AHG中，
，∴△ABG≌△AHG（ASA），
∴AH=AB=4，∠ABG=∠AHG，
∴HD=AD﹣AH=6﹣4=2，
∵AB∥MF，∴∠ABG=∠M，
∵∠AHG=∠MHD，∴∠M=∠MHD，∴DM=DH=2，
同理可得：CF=CE=2，
∴MF=DM+CD+CF=2+4+2=8．