三角形的中位线 练习(基础题)
图片预览
文档简介
三角形的中位线
一.解答题(共6小题)
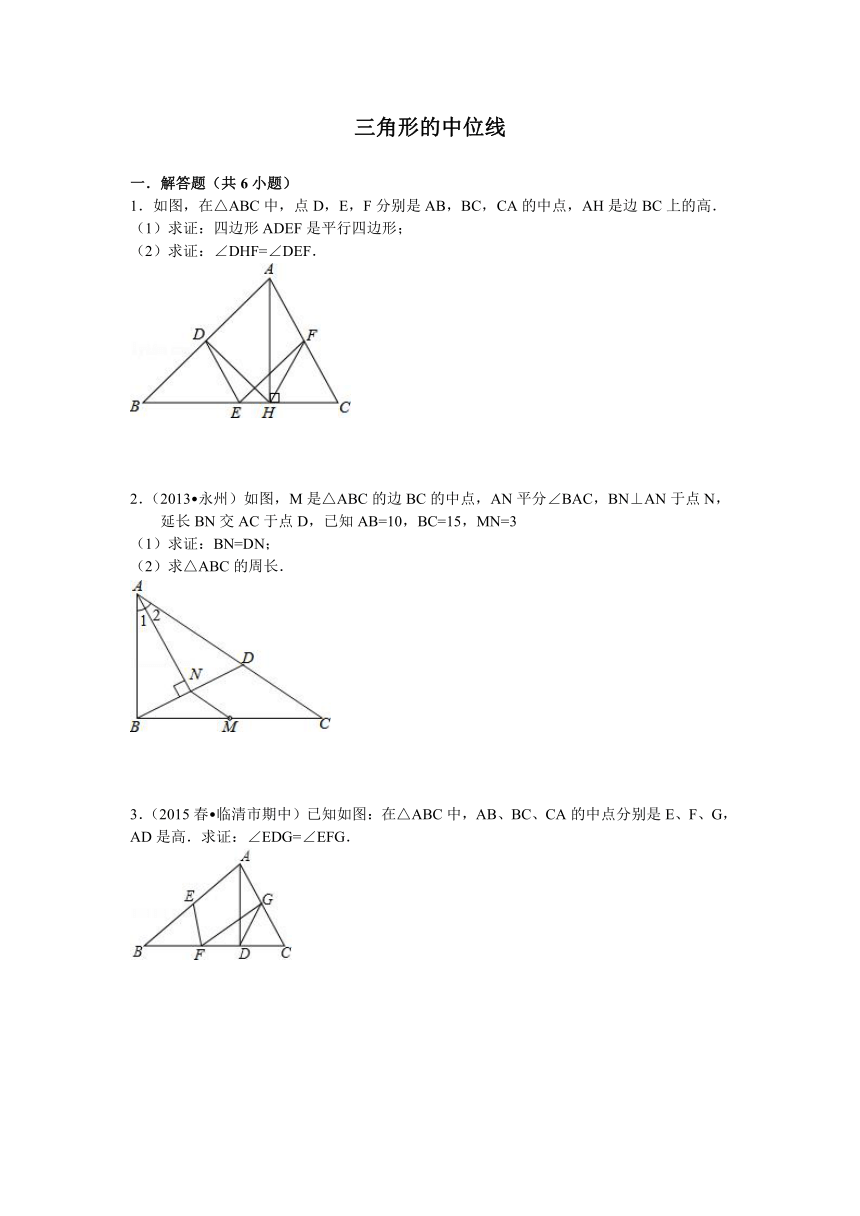
1.如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
(1)求证:四边形ADEF是平行四边形;
(2)求证:∠DHF=∠DEF.
( http: / / www.21cnjy.com )
2.(2013 永州)如图,M是△ABC
( http: / / www.21cnjy.com )的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
(1)求证:BN=DN;
(2)求△ABC的周长.
( http: / / www.21cnjy.com )
3.(2015春 临清市期中)已知如图:在△ABC中,AB、BC、CA的中点分别是E、F、G,AD是高.求证:∠EDG=∠EFG.
( http: / / www.21cnjy.com )
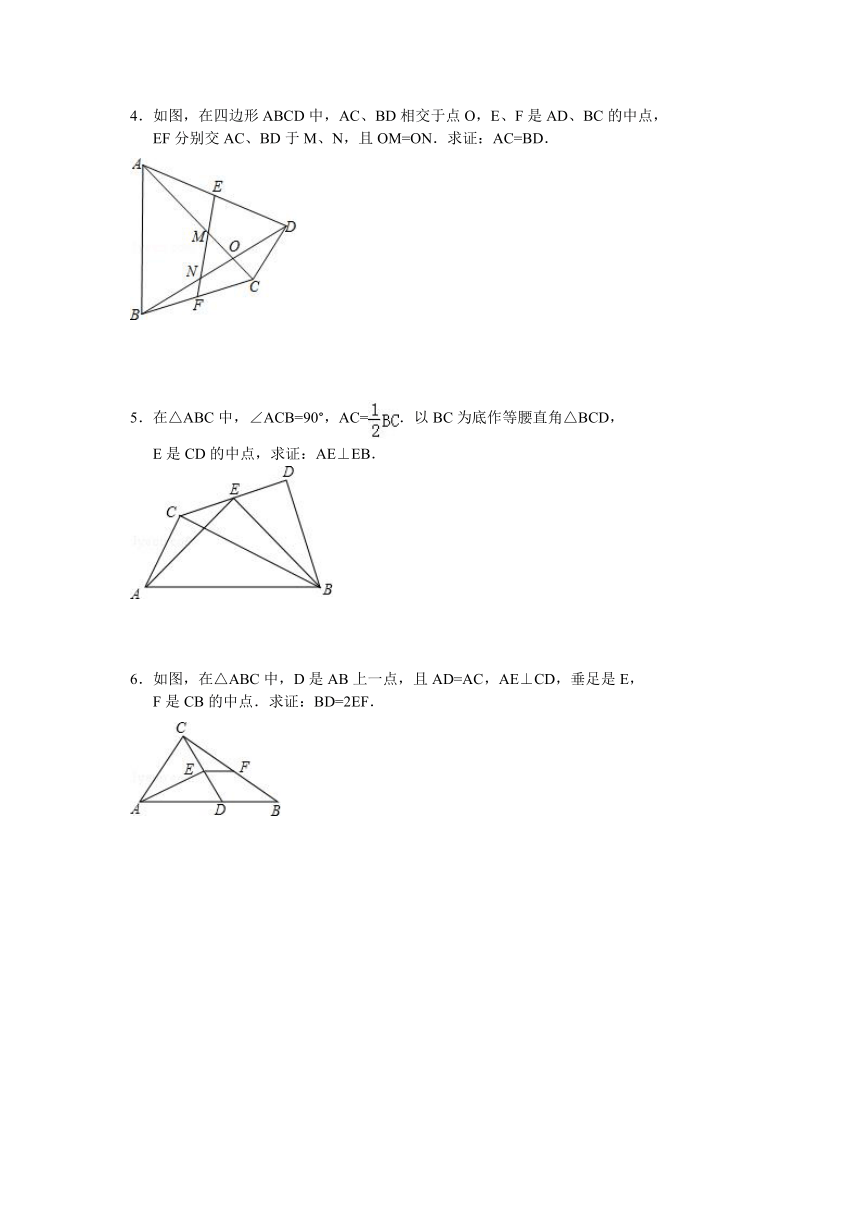
4.如图,在四边形ABCD中,AC、BD相交于点O,E、F是AD、BC的中点,
EF分别交AC、BD于M、N,且OM=ON.求证:AC=BD.
( http: / / www.21cnjy.com )
5.在△ABC中,∠ACB=90°,AC=.以BC为底作等腰直角△BCD,
E是CD的中点,求证:AE⊥EB.
( http: / / www.21cnjy.com )
6.如图,在△ABC中,D是AB上一点,且AD=AC,AE⊥CD,垂足是E,
F是CB的中点.求证:BD=2EF.
( http: / / www.21cnjy.com )
参考答案与试题解析
一.解答题(共6小题)
1.【解答】证明:(1)∵点D,E,F分别是AB,BC,CA的中点,
∴DE、EF都是△ABC的中位线,∴EF∥AB,DE∥AC,∴四边形ADEF是平行四边形;
(2)∵四边形ADEF是平行四边形,∴∠DEF=∠BAC,
∵D,F分别是AB,CA的中点,AH是边BC上的高,∴DH=AD,FH=AF,
∴∠DAH=∠DHA,∠FAH=∠FHA,
∵∠DAH+∠FAH=∠BAC,∠DHA+∠FHA=∠DHF,
∴∠DHF=∠BAC,∴∠DHF=∠DEF.
2.【解答】(1)证明:在△ABN和△ADN中,
∵,∴△ABN≌△ADN(ASA),∴BN=DN.
(2)解:∵△ABN≌△ADN,∴AD=AB=10,
又∵点M是BC中点,∴MN是△BDC的中位线,∴CD=2MN=6,
3.【解答】证明:连接EG,
∵E、F、G分别是AB、BC、CA的中点,∴EF为△ABC的中位线,EF=AC.
(三角形的中位线等于第三边的一半)
又∵AD⊥BC,∴∠ADC=90°,DG为直角△ADC斜边上的中线,
∴DG=AC.(直角三角形斜边上的中线等于斜边的一半)
∴DG=EF.
同理DE=FG,EG=GE,∴△EFG≌△GDE(SSS).∴∠EDG=∠EFG.
4.【解答】证明:取AB和CD的中点分别为G、H,连接EG、GF、FH、EH,
则EH∥AC,EH=AC,HF∥BD,FH=BD,∴∠3=∠2,∠1=∠4,
∵OM=ON,∴∠1=∠2,∴∠4=∠3=∠1=∠2,
同理∠EFH=∠GFE=∠1=∠2,∴∠4=∠EFH,∴EH=HF,
∵EH=AC,FH=BD,∴AC=BD.
5.【解答】证明:过E作EF∥BC交BD于F.
∵∠ACE=∠ACB+∠BCE=135°,∠DFE=∠DBC=45°,∴∠EFB=135°.
又EF=BC,EF∥BC,AC=BC,∴EF=AC,CE=FB.
∴△EFB≌△ACE.∴∠CEA=∠DBE.
又∵∠DBE+∠DEB=90°,∴∠DEB+∠CEA=90°.故∠AEB=90°.∴AE⊥EB.
6.【解答】证明:在△ACD中,因为AD=AC
且
AE⊥CD,
所以根据等腰三角形中底边的垂线与底边的交点即中点,可以证明:
E为CD的中点,又因为F是CB的中点,
所以,EF∥BD,且EF为△BCD的中位线,
因此EF=BD,即BD=2EF.
一.解答题(共6小题)
1.如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
(1)求证:四边形ADEF是平行四边形;
(2)求证:∠DHF=∠DEF.
( http: / / www.21cnjy.com )
2.(2013 永州)如图,M是△ABC
( http: / / www.21cnjy.com )的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
(1)求证:BN=DN;
(2)求△ABC的周长.
( http: / / www.21cnjy.com )
3.(2015春 临清市期中)已知如图:在△ABC中,AB、BC、CA的中点分别是E、F、G,AD是高.求证:∠EDG=∠EFG.
( http: / / www.21cnjy.com )
4.如图,在四边形ABCD中,AC、BD相交于点O,E、F是AD、BC的中点,
EF分别交AC、BD于M、N,且OM=ON.求证:AC=BD.
( http: / / www.21cnjy.com )
5.在△ABC中,∠ACB=90°,AC=.以BC为底作等腰直角△BCD,
E是CD的中点,求证:AE⊥EB.
( http: / / www.21cnjy.com )
6.如图,在△ABC中,D是AB上一点,且AD=AC,AE⊥CD,垂足是E,
F是CB的中点.求证:BD=2EF.
( http: / / www.21cnjy.com )
参考答案与试题解析
一.解答题(共6小题)
1.【解答】证明:(1)∵点D,E,F分别是AB,BC,CA的中点,
∴DE、EF都是△ABC的中位线,∴EF∥AB,DE∥AC,∴四边形ADEF是平行四边形;
(2)∵四边形ADEF是平行四边形,∴∠DEF=∠BAC,
∵D,F分别是AB,CA的中点,AH是边BC上的高,∴DH=AD,FH=AF,
∴∠DAH=∠DHA,∠FAH=∠FHA,
∵∠DAH+∠FAH=∠BAC,∠DHA+∠FHA=∠DHF,
∴∠DHF=∠BAC,∴∠DHF=∠DEF.
2.【解答】(1)证明:在△ABN和△ADN中,
∵,∴△ABN≌△ADN(ASA),∴BN=DN.
(2)解:∵△ABN≌△ADN,∴AD=AB=10,
又∵点M是BC中点,∴MN是△BDC的中位线,∴CD=2MN=6,
3.【解答】证明:连接EG,
∵E、F、G分别是AB、BC、CA的中点,∴EF为△ABC的中位线,EF=AC.
(三角形的中位线等于第三边的一半)
又∵AD⊥BC,∴∠ADC=90°,DG为直角△ADC斜边上的中线,
∴DG=AC.(直角三角形斜边上的中线等于斜边的一半)
∴DG=EF.
同理DE=FG,EG=GE,∴△EFG≌△GDE(SSS).∴∠EDG=∠EFG.
4.【解答】证明:取AB和CD的中点分别为G、H,连接EG、GF、FH、EH,
则EH∥AC,EH=AC,HF∥BD,FH=BD,∴∠3=∠2,∠1=∠4,
∵OM=ON,∴∠1=∠2,∴∠4=∠3=∠1=∠2,
同理∠EFH=∠GFE=∠1=∠2,∴∠4=∠EFH,∴EH=HF,
∵EH=AC,FH=BD,∴AC=BD.
5.【解答】证明:过E作EF∥BC交BD于F.
∵∠ACE=∠ACB+∠BCE=135°,∠DFE=∠DBC=45°,∴∠EFB=135°.
又EF=BC,EF∥BC,AC=BC,∴EF=AC,CE=FB.
∴△EFB≌△ACE.∴∠CEA=∠DBE.
又∵∠DBE+∠DEB=90°,∴∠DEB+∠CEA=90°.故∠AEB=90°.∴AE⊥EB.
6.【解答】证明:在△ACD中,因为AD=AC
且
AE⊥CD,
所以根据等腰三角形中底边的垂线与底边的交点即中点,可以证明:
E为CD的中点,又因为F是CB的中点,
所以,EF∥BD,且EF为△BCD的中位线,
因此EF=BD,即BD=2EF.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
