浙教版八下数学4.2平行四边形及其性质(2)
文档属性
| 名称 | 浙教版八下数学4.2平行四边形及其性质(2) |
|
|
| 格式 | zip | ||
| 文件大小 | 139.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-07 16:42:49 | ||
图片预览



文档简介
浙教版八下数学4.2平行四边形及其性质(2)
一.选择题(共9小题)
1.若一个多边形的每个内角都等于108°,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形
2.某多边形的内角和是其外角和的3倍,则此多边形的边数是( )
A.5 B.6 C.7 D.8
3.一个多边形的内角和与外角和的比为5:2,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
4.多边形的内角中,锐角的个数最多有( )
A.1个 B.2个 C.3个 D.4个
5.一个多边形除一个内角外其余内角的和为1510°,则这个多边形对角线的条数是( )
A.27 B.35 C.44 D.54
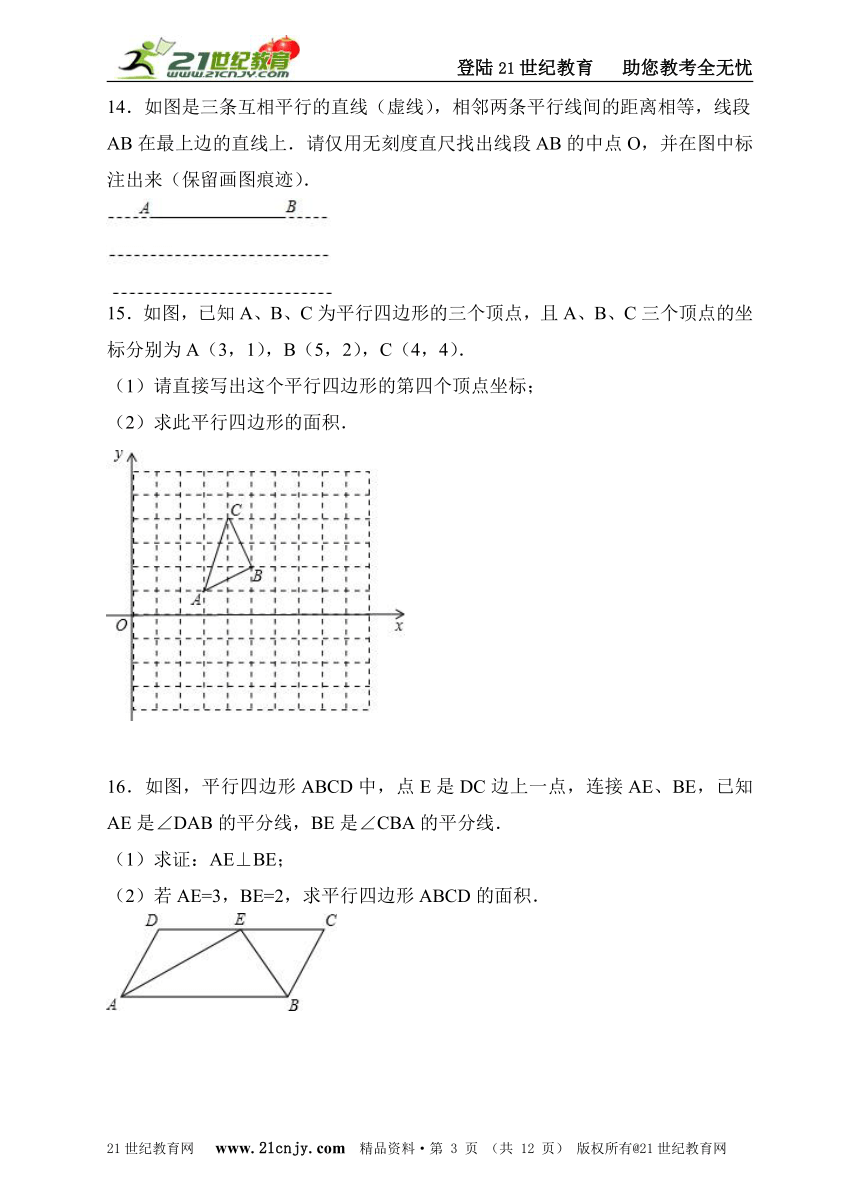
6.如图,4×4的方格中每个小正方形的边长都是1,则S四边形ABCD与S四边形ECDF的大小关系是( )21世纪教育网版权所有
A.S四边形ABDC=S四边形ECDF B.S四边形ABDC<S四边形ECDF21cnjy.com
C.S四边形ABDC=S四边形ECDF+1 D.S四边形ABDC=S四边形ECDF+2
7.一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )
A.90° B.100° C.130° D.180°
8.某广场上一个形状是平行四边形的花坛,分别种有红、黄、蓝、白、橙、紫6种颜色的花.如果有AB∥EF∥DC,BC∥GH∥AD,那么下列说法中错误的是( )21·cn·jy·com
红花,绿花种植面积一定相等
B.红花,蓝花种植面积一定相等
C.蓝花,黄花种植面积一定相等
D.紫花,橙花种植面积一定相等
9.如图,在平行四边形ABCD中,E是BC中点,S四边形ABCD=24,AF=2FB,FE的延长线与DC的延长线相交于点H,则△DEF的面积是( )
A.8 B.16 C.12 D.10
二.填空题(共4小题)
10.命题“夹在两条平行线间的相等线段平行”是 命题(填“真”或“假”).
11.一个多边形的对角线的条数与它的边数相等,则这个多边形的内角和为 .
12.从一个多边形的一个顶点出发,作了15条对角线,则这个多边形的内角和为 度.
13.在?ABCD中,AB=15,AD=9,AB和CD之间的距离为6,则AD和BC之间的距离为 .www.21-cn-jy.com
三.解答题(共5小题)
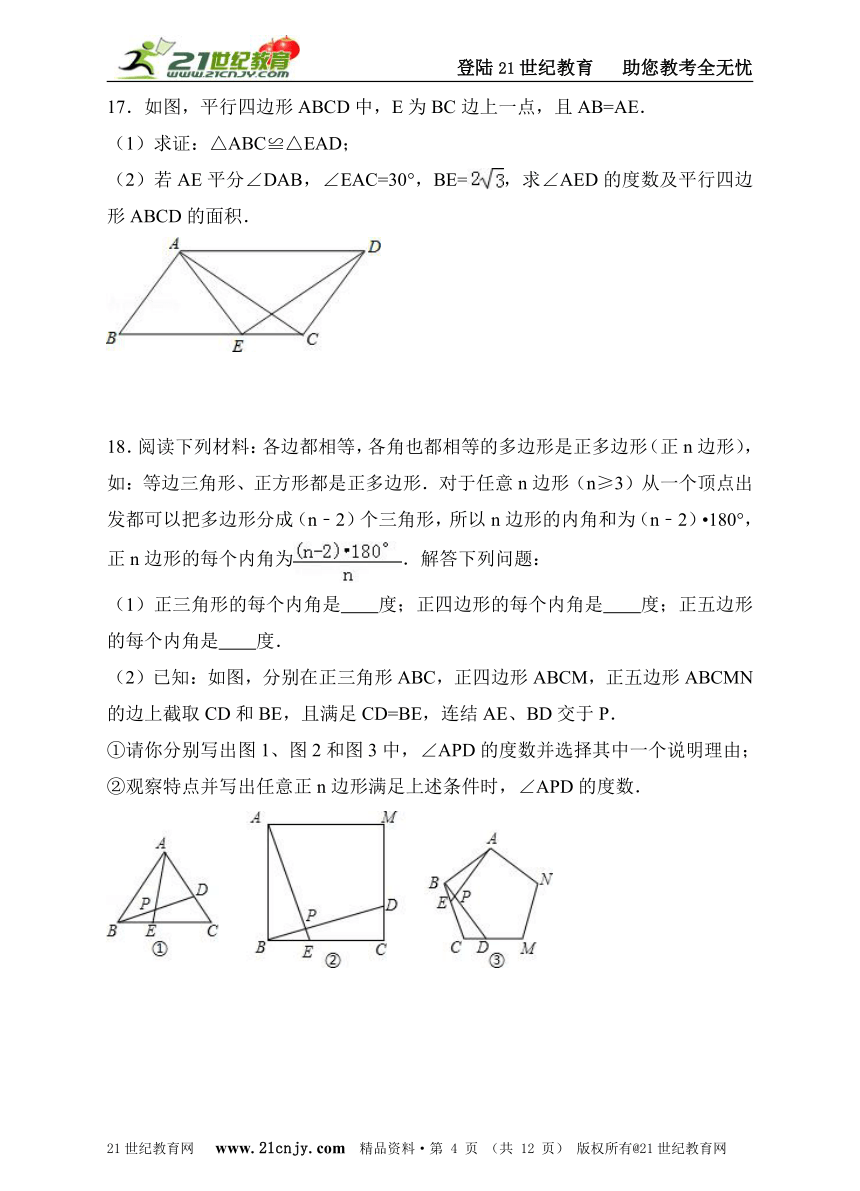
14.如图是三条互相平行的直线(虚线),相邻两条平行线间的距离相等,线段AB在最上边的直线上.请仅用无刻度直尺找出线段AB的中点O,并在图中标注出来(保留画图痕迹).2·1·c·n·j·y
15.如图,已知A、B、C为平行四边形的三个顶点,且A、B、C三个顶点的坐标分别为A(3,1),B(5,2),C(4,4).【来源:21·世纪·教育·网】
(1)请直接写出这个平行四边形的第四个顶点坐标;
(2)求此平行四边形的面积.
16.如图,平行四边形ABCD中,点E是DC边上一点,连接AE、BE,已知AE是∠DAB的平分线,BE是∠CBA的平分线.21·世纪*教育网
(1)求证:AE⊥BE;
(2)若AE=3,BE=2,求平行四边形ABCD的面积.
17.如图,平行四边形ABCD中,E为BC边上一点,且AB=AE.
(1)求证:△ABC≌△EAD;
(2)若AE平分∠DAB,∠EAC=30°,BE=,求∠AED的度数及平行四边形ABCD的面积.
18.阅读下列材料:各边都相等,各角也都相等的多边形是正多边形(正n边形),如:等边三角形、正方形都是正多边形.对于任意n边形(n≥3)从一个顶点出发都可以把多边形分成(n﹣2)个三角形,所以n边形的内角和为(n﹣2)?180°,正n边形的每个内角为.解答下列问题:www-2-1-cnjy-com
(1)正三角形的每个内角是 度;正四边形的每个内角是 度;正五边形的每个内角是 度.
(2)已知:如图,分别在正三角形ABC,正四边形ABCM,正五边形ABCMN的边上截取CD和BE,且满足CD=BE,连结AE、BD交于P.
①请你分别写出图1、图2和图3中,∠APD的度数并选择其中一个说明理由;
②观察特点并写出任意正n边形满足上述条件时,∠APD的度数.
浙教版八下数学4.2平行四边形及其性质(2)
参考答案与试题解析
一.选择题(共9小题)
1.解:设这个多边形是n边形,
由题意得,(n﹣2)?180°=108°?n,
解得n=5,
所以,这个多边形是五边形.
故选B.
2.解:根据题意,得:(n﹣2)×180=360×3,解得n=8.
故选D.
3.解:设这个多边形是n边形.
则[(n﹣2)×180°]:360°=5:2,
n=7.
故这个多边形是七边形.
故选C.
4.解:因为多边形的外角和是360度,在外角中最多有三个钝角,如果超过三个则和一定大于360度,
多边形的内角与外角互为邻补角,则外角中最多有三个钝角,内角中就最多有3个锐角.
故选C.
5.解:设这个内角度数为x°,边数为n,
∴(n﹣2)×180﹣x=1510,
180n=1870+x,
∵n为正整数,
∴n=11,
∴=44,
故选:C.
6.解:S四边形ABDC=CD?AC=1×4=4,
S四边形ECDF=CD?AC=1×4=4,
故选:A.
7.解:如图,∠BAC=180°﹣90°﹣∠1=90°﹣∠1,
∠ABC=180°﹣60°﹣∠3=120°﹣∠3,
∠ACB=180°﹣60°﹣∠2=120°﹣∠2,
在△ABC中,∠BAC+∠ABC+∠ACB=180°,
∴90°﹣∠1+120°﹣∠3+120°﹣∠2=180°,
∴∠1+∠2=150°﹣∠3,
∵∠3=50°,
∴∠1+∠2=150°﹣50°=100°.
故选:B.
8.解:如图所示:
∵AB∥EF∥DC,BC∥GH∥AD,
∴四边形ABCD、四边形DEOH、四边形BGOF、四边形AGOE、四边形CHOF是平行四边形,
∴△ABD的面积=△CBD的面积,△DOE的面积=△DOH的面积,△BOG的面积=△BOF的面积,
∴四边形AGOE的面积=四边形CHOF的面积,
∴A、C、D正确,B不正确;
故选:B.
9.解:设AD的长为a,点A到边BC的距离为h,
∵在平行四边形ABCD中,E是BC中点,S四边形ABCD=24,AF=2FB,
∴S△DEF=S四边形ABCD﹣S△BEF﹣S△CED﹣S△ADF=24﹣=24﹣2﹣6﹣8=8,21教育网
故选A.
二.填空题(共4小题)
10.解:矩形的对角线是夹在两条平行线间的相等线段,但它们不平行,
所以命题“夹在两条平行线间的相等线段平行”是假命题.
故答案为假.
11.解:设多边形有n条边,
则=n,
解得n=5或n=0(应舍去).
故这个多边形的边数是5.
故答案为:5.
12.解:设这个多边形的边数为n,
由题意得,n﹣3=15,
解得,n=18,
(18﹣2)×180°=2880°,
故答案为:2880.
13.解:由题意得,S四边形ABCD=AB×DE=BC×DF,
∴15×6=9×DF,
∴DF=10,即AD与BC之间的距离为10.
故答案为:10.
三.解答题(共5小题)
14.解:作法:1.过点A任意作一条直线AC交第三条直线于点C,交第二条直线于点D,
2.连接BC交第二条直线于E,连接BD,AE交于点M,作射线CM交AB于点O,
则点O就是要求作的点.
15.解:(1)如图:(6,5),(4,﹣1),(2,3);
(2)如图:S=S矩形AEDF﹣S△ABM﹣S△BND﹣S△CGD﹣S△ACH﹣S正方形FHCG﹣S正方形BMEN=3×4﹣×1×2﹣×1×2﹣×1×2﹣×1×3﹣1×1﹣1×1=5.
16.解:(1)∵四边形ABCD是平行四边形,
∴∠ABC+∠BAD=180°,
∵BE、AE分别平分∠ABC和∠BAD,
∴∠ABE+∠BAE=90°,
∴∠AEB=90°,
即AE⊥BE;
(2)∵AE⊥BE
∴S△ABE=AE×BE÷2=3,
∴平行四边形ABCD的面积=2S△ABE=6.
17.(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC.
∴∠DAE=∠AEB.
∵AB=AE,
∴∠AEB=∠B.
∴∠B=∠DAE.
∴△ABC≌△EAD.
(2)解:过点A作AE⊥BC于H,
∵AE平分∠DAB,
∴∠BAE=∠DAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴AB=BE,
∵AB=AE,
∴△ABE是等边三角形,
∴∠BAE=60°,
∵∠EAC=30°,
∴∠BAC=90°,
∵△ABC≌△EAD,
∴∠AED=∠BAC=90°,
∵BE=2,
∴AH=3,
∵AB=BC,
∴BC=4,
∴S四边形ABCD=3×4=12.
18.解:(1)正三角形的每个内角是:=60°;
正四边形的每个内角是:=90°;
正五边形的每个内角是:=108°.
故答案是:60;90;108;
(2)①如图①,∠APD=60°,理由如下:
∵△ABC是等边三角形,
∴AB=BC,∠ABE=∠BCD=60°.
∵在△ABE与△BCD中,,
∴△ABE≌△BCD(SAS).
∴∠BAE=∠CBD.
∴∠APD=∠ABP+∠BAE=∠ABP+∠CBD=∠ABE=60°.
如图②,∠APD=90°,理由如下:
同理可证:△ABE≌△BCD,
∴∠AEB+∠DBC=180°﹣90°=90°,
∴∠APD=∠BPE=180°﹣90°=90°;
如图③,∠APD=108°,理由如下:
同理可证:△ABE≌△BCD,
∴∠AEB+∠DBC=180°﹣108°=72°,
∴∠APD=∠BPE=180°﹣(∠AEB+∠DBC)=180°﹣72°=108°.
②能.如图④,点E、D分别是正n边形ABCM中以C点为顶点的相邻两边上的点,且BE=CD,BD与AE交于点P,则∠APD的度数为.
一.选择题(共9小题)
1.若一个多边形的每个内角都等于108°,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形
2.某多边形的内角和是其外角和的3倍,则此多边形的边数是( )
A.5 B.6 C.7 D.8
3.一个多边形的内角和与外角和的比为5:2,则这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
4.多边形的内角中,锐角的个数最多有( )
A.1个 B.2个 C.3个 D.4个
5.一个多边形除一个内角外其余内角的和为1510°,则这个多边形对角线的条数是( )
A.27 B.35 C.44 D.54
6.如图,4×4的方格中每个小正方形的边长都是1,则S四边形ABCD与S四边形ECDF的大小关系是( )21世纪教育网版权所有
A.S四边形ABDC=S四边形ECDF B.S四边形ABDC<S四边形ECDF21cnjy.com
C.S四边形ABDC=S四边形ECDF+1 D.S四边形ABDC=S四边形ECDF+2
7.一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )
A.90° B.100° C.130° D.180°
8.某广场上一个形状是平行四边形的花坛,分别种有红、黄、蓝、白、橙、紫6种颜色的花.如果有AB∥EF∥DC,BC∥GH∥AD,那么下列说法中错误的是( )21·cn·jy·com
红花,绿花种植面积一定相等
B.红花,蓝花种植面积一定相等
C.蓝花,黄花种植面积一定相等
D.紫花,橙花种植面积一定相等
9.如图,在平行四边形ABCD中,E是BC中点,S四边形ABCD=24,AF=2FB,FE的延长线与DC的延长线相交于点H,则△DEF的面积是( )
A.8 B.16 C.12 D.10
二.填空题(共4小题)
10.命题“夹在两条平行线间的相等线段平行”是 命题(填“真”或“假”).
11.一个多边形的对角线的条数与它的边数相等,则这个多边形的内角和为 .
12.从一个多边形的一个顶点出发,作了15条对角线,则这个多边形的内角和为 度.
13.在?ABCD中,AB=15,AD=9,AB和CD之间的距离为6,则AD和BC之间的距离为 .www.21-cn-jy.com
三.解答题(共5小题)
14.如图是三条互相平行的直线(虚线),相邻两条平行线间的距离相等,线段AB在最上边的直线上.请仅用无刻度直尺找出线段AB的中点O,并在图中标注出来(保留画图痕迹).2·1·c·n·j·y
15.如图,已知A、B、C为平行四边形的三个顶点,且A、B、C三个顶点的坐标分别为A(3,1),B(5,2),C(4,4).【来源:21·世纪·教育·网】
(1)请直接写出这个平行四边形的第四个顶点坐标;
(2)求此平行四边形的面积.
16.如图,平行四边形ABCD中,点E是DC边上一点,连接AE、BE,已知AE是∠DAB的平分线,BE是∠CBA的平分线.21·世纪*教育网
(1)求证:AE⊥BE;
(2)若AE=3,BE=2,求平行四边形ABCD的面积.
17.如图,平行四边形ABCD中,E为BC边上一点,且AB=AE.
(1)求证:△ABC≌△EAD;
(2)若AE平分∠DAB,∠EAC=30°,BE=,求∠AED的度数及平行四边形ABCD的面积.
18.阅读下列材料:各边都相等,各角也都相等的多边形是正多边形(正n边形),如:等边三角形、正方形都是正多边形.对于任意n边形(n≥3)从一个顶点出发都可以把多边形分成(n﹣2)个三角形,所以n边形的内角和为(n﹣2)?180°,正n边形的每个内角为.解答下列问题:www-2-1-cnjy-com
(1)正三角形的每个内角是 度;正四边形的每个内角是 度;正五边形的每个内角是 度.
(2)已知:如图,分别在正三角形ABC,正四边形ABCM,正五边形ABCMN的边上截取CD和BE,且满足CD=BE,连结AE、BD交于P.
①请你分别写出图1、图2和图3中,∠APD的度数并选择其中一个说明理由;
②观察特点并写出任意正n边形满足上述条件时,∠APD的度数.
浙教版八下数学4.2平行四边形及其性质(2)
参考答案与试题解析
一.选择题(共9小题)
1.解:设这个多边形是n边形,
由题意得,(n﹣2)?180°=108°?n,
解得n=5,
所以,这个多边形是五边形.
故选B.
2.解:根据题意,得:(n﹣2)×180=360×3,解得n=8.
故选D.
3.解:设这个多边形是n边形.
则[(n﹣2)×180°]:360°=5:2,
n=7.
故这个多边形是七边形.
故选C.
4.解:因为多边形的外角和是360度,在外角中最多有三个钝角,如果超过三个则和一定大于360度,
多边形的内角与外角互为邻补角,则外角中最多有三个钝角,内角中就最多有3个锐角.
故选C.
5.解:设这个内角度数为x°,边数为n,
∴(n﹣2)×180﹣x=1510,
180n=1870+x,
∵n为正整数,
∴n=11,
∴=44,
故选:C.
6.解:S四边形ABDC=CD?AC=1×4=4,
S四边形ECDF=CD?AC=1×4=4,
故选:A.
7.解:如图,∠BAC=180°﹣90°﹣∠1=90°﹣∠1,
∠ABC=180°﹣60°﹣∠3=120°﹣∠3,
∠ACB=180°﹣60°﹣∠2=120°﹣∠2,
在△ABC中,∠BAC+∠ABC+∠ACB=180°,
∴90°﹣∠1+120°﹣∠3+120°﹣∠2=180°,
∴∠1+∠2=150°﹣∠3,
∵∠3=50°,
∴∠1+∠2=150°﹣50°=100°.
故选:B.
8.解:如图所示:
∵AB∥EF∥DC,BC∥GH∥AD,
∴四边形ABCD、四边形DEOH、四边形BGOF、四边形AGOE、四边形CHOF是平行四边形,
∴△ABD的面积=△CBD的面积,△DOE的面积=△DOH的面积,△BOG的面积=△BOF的面积,
∴四边形AGOE的面积=四边形CHOF的面积,
∴A、C、D正确,B不正确;
故选:B.
9.解:设AD的长为a,点A到边BC的距离为h,
∵在平行四边形ABCD中,E是BC中点,S四边形ABCD=24,AF=2FB,
∴S△DEF=S四边形ABCD﹣S△BEF﹣S△CED﹣S△ADF=24﹣=24﹣2﹣6﹣8=8,21教育网
故选A.
二.填空题(共4小题)
10.解:矩形的对角线是夹在两条平行线间的相等线段,但它们不平行,
所以命题“夹在两条平行线间的相等线段平行”是假命题.
故答案为假.
11.解:设多边形有n条边,
则=n,
解得n=5或n=0(应舍去).
故这个多边形的边数是5.
故答案为:5.
12.解:设这个多边形的边数为n,
由题意得,n﹣3=15,
解得,n=18,
(18﹣2)×180°=2880°,
故答案为:2880.
13.解:由题意得,S四边形ABCD=AB×DE=BC×DF,
∴15×6=9×DF,
∴DF=10,即AD与BC之间的距离为10.
故答案为:10.
三.解答题(共5小题)
14.解:作法:1.过点A任意作一条直线AC交第三条直线于点C,交第二条直线于点D,
2.连接BC交第二条直线于E,连接BD,AE交于点M,作射线CM交AB于点O,
则点O就是要求作的点.
15.解:(1)如图:(6,5),(4,﹣1),(2,3);
(2)如图:S=S矩形AEDF﹣S△ABM﹣S△BND﹣S△CGD﹣S△ACH﹣S正方形FHCG﹣S正方形BMEN=3×4﹣×1×2﹣×1×2﹣×1×2﹣×1×3﹣1×1﹣1×1=5.
16.解:(1)∵四边形ABCD是平行四边形,
∴∠ABC+∠BAD=180°,
∵BE、AE分别平分∠ABC和∠BAD,
∴∠ABE+∠BAE=90°,
∴∠AEB=90°,
即AE⊥BE;
(2)∵AE⊥BE
∴S△ABE=AE×BE÷2=3,
∴平行四边形ABCD的面积=2S△ABE=6.
17.(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC.
∴∠DAE=∠AEB.
∵AB=AE,
∴∠AEB=∠B.
∴∠B=∠DAE.
∴△ABC≌△EAD.
(2)解:过点A作AE⊥BC于H,
∵AE平分∠DAB,
∴∠BAE=∠DAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴AB=BE,
∵AB=AE,
∴△ABE是等边三角形,
∴∠BAE=60°,
∵∠EAC=30°,
∴∠BAC=90°,
∵△ABC≌△EAD,
∴∠AED=∠BAC=90°,
∵BE=2,
∴AH=3,
∵AB=BC,
∴BC=4,
∴S四边形ABCD=3×4=12.
18.解:(1)正三角形的每个内角是:=60°;
正四边形的每个内角是:=90°;
正五边形的每个内角是:=108°.
故答案是:60;90;108;
(2)①如图①,∠APD=60°,理由如下:
∵△ABC是等边三角形,
∴AB=BC,∠ABE=∠BCD=60°.
∵在△ABE与△BCD中,,
∴△ABE≌△BCD(SAS).
∴∠BAE=∠CBD.
∴∠APD=∠ABP+∠BAE=∠ABP+∠CBD=∠ABE=60°.
如图②,∠APD=90°,理由如下:
同理可证:△ABE≌△BCD,
∴∠AEB+∠DBC=180°﹣90°=90°,
∴∠APD=∠BPE=180°﹣90°=90°;
如图③,∠APD=108°,理由如下:
同理可证:△ABE≌△BCD,
∴∠AEB+∠DBC=180°﹣108°=72°,
∴∠APD=∠BPE=180°﹣(∠AEB+∠DBC)=180°﹣72°=108°.
②能.如图④,点E、D分别是正n边形ABCM中以C点为顶点的相邻两边上的点,且BE=CD,BD与AE交于点P,则∠APD的度数为.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
