4.2平行四边形及其性质（3）

浙教版八下4.2平行四边形及其性质（3）
　
一．选择题（共5小题）
1．如图，?ABCD的对角线AC、BD相交于点O，则下列说法一定正确的是（　　）
A．AO=OD B．AO⊥OD C．AO=OC D．AO⊥AB
2．如图，在?ABCD中，已知AD=12cm，AB=8cm，AE平分∠BAD交BC边于点E，则CE的长等于（　　）www.21-cn-jy.com
A．8cm B．6cm C．4cm D．2cm
3．平行四边形ABCD中，对角线AC、BD交于点O（如图），则图中全等三角形的对数为（　　）
A．2 B．3 C．4 D．5
4．如图，平行四边形ABCD中，E，F是对角线BD上的两点，如果添加一个条件使△ABE≌△CDF，则添加的条件是（　　）2·1·c·n·j·y
A．AE=CF B．BE=FD C．BF=DE D．∠1=∠2
5．如图，在平行四边形ABCD中，对角线AC、BD相交于点O．如果BD=12，AC=10，BC=m，那么m的取值范围是（　　）【来源：21·世纪·教育·网】
A．10＜m＜12 B．2＜m＜22 C．1＜m＜11 D．5＜m＜6
　
二．填空题（共4小题）
6．已知矩形的周长为40cm，被两条对角线分成的相邻两个三角形的周长的差为8cm，则较大的边长为　　．21·世纪*教育网
7．如图，?ABCD的面积为24，EF，GH过AC，BD的交点O，则图中阴影部分的面积为　　．
8．如图，平行四边形ABCD的周长为16cm，AC，BD相交于点O，OE⊥AC于O，则△DCE的周长为　　cm．www-2-1-cnjy-com
9．如图，?ABCD的面积为16，对角线交于点O；以AB、AO为邻边作?AOC1B，对角线交于点O1；以AB、AO1为邻边作?AO1C2B，对角线交于点O2；…；依此类推．则?AOC1B的面积为　　；?AO4C5B的面积为　　；?AOnCn+1B的面积为　　．2-1-c-n-j-y
　
三．解答题（共7小题）
10．如图，若平行四边形ABCD的周长为22cm，AC、BD相交于点0，△A0D的周长比△ABO的周长小3cm，求AD，AB的长．21·cn·jy·com
11．如图所示，在平行四边形ABCD中，对角线AC与BD相交于点O，M，N在对角线AC上，且AM=CN，求证：BM∥DN．21*cnjy*com
12．如图，?ABCD的对角线AC、BD相交于点O，E，F分别是OA，OC的中点，连接BE，DF
（1）根据题意，补全图形；
（2）求证：BE=DF．
13．如图，平行四边形ABCD的对角线AC、BD，相交于点O，EF过点O且与AB、CD分别相交于点E、F，求证：AE=CF．21cnjy.com
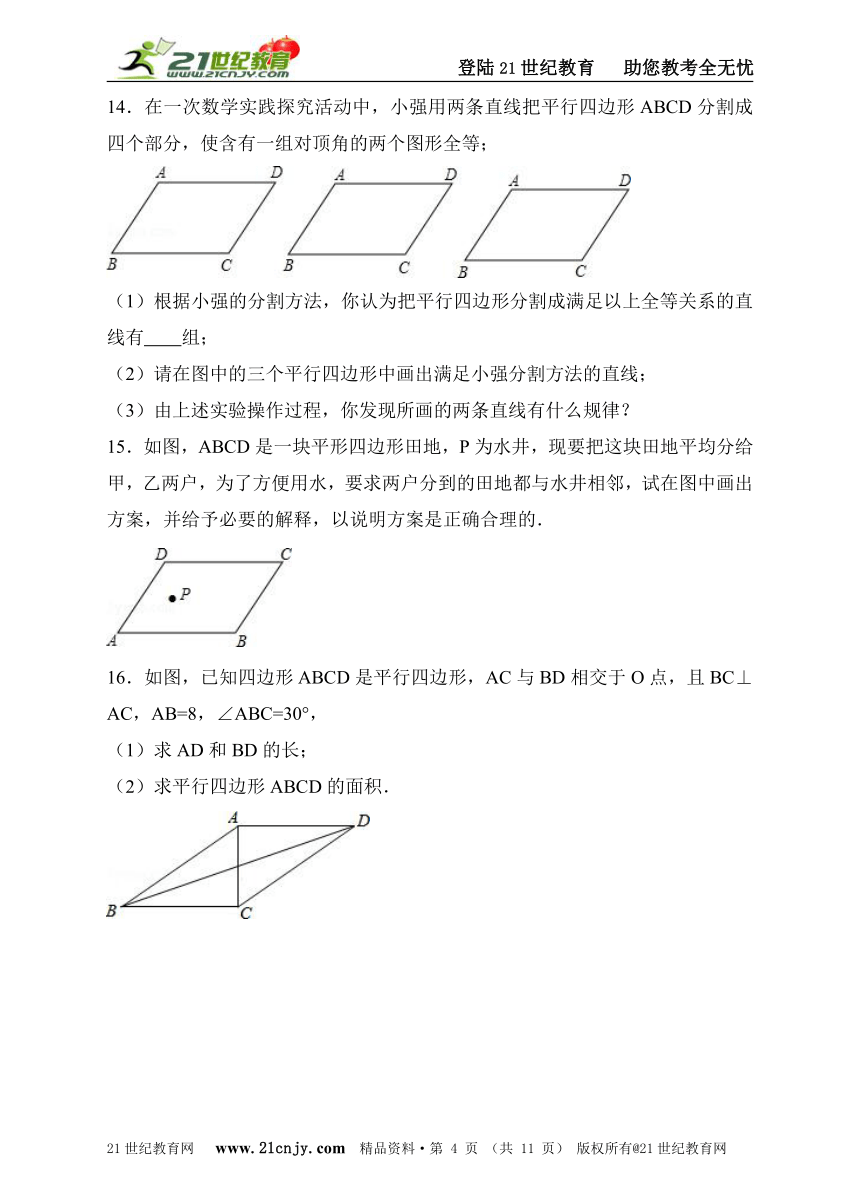
14．在一次数学实践探究活动中，小强用两条直线把平行四边形ABCD分割成四个部分，使含有一组对顶角的两个图形全等；【来源：21cnj*y.co*m】
（1）根据小强的分割方法，你认为把平行四边形分割成满足以上全等关系的直线有　　组；
（2）请在图中的三个平行四边形中画出满足小强分割方法的直线；
（3）由上述实验操作过程，你发现所画的两条直线有什么规律？
15．如图，ABCD是一块平形四边形田地，P为水井，现要把这块田地平均分给甲，乙两户，为了方便用水，要求两户分到的田地都与水井相邻，试在图中画出方案，并给予必要的解释，以说明方案是正确合理的．【出处：21教育名师】
16．如图，已知四边形ABCD是平行四边形，AC与BD相交于O点，且BC⊥AC，AB=8，∠ABC=30°，【版权所有：21教育】
（1）求AD和BD的长；
（2）求平行四边形ABCD的面积．
　

浙教版八下4.2平行四边形及其性质（3）
参考答案与试题解析
　
一．选择题（共5小题）
1．解：对角线不一定相等，A错误；
对角线不一定互相垂直，B错误；
对角线互相平分，C正确；
对角线与边不一定垂直，D错误．
故选：C．
　
2．解：∵四边形ABCD是平行四边形，
∴BC=AD=12cm，AD∥BC，
∴∠DAE=∠BEA，
∵AE平分∠BAD，
∴∠BAE=∠DAE，
∴∠BEA=∠BAE，
∴BE=AB=8cm，
∴CE=BC﹣BE=4cm；
故答案为：C．
　
3．解：∵四边形ABCD是平行四边形，
∴AB=CD，AD=BC；OD=OB，OA=OC；
∵OD=OB，OA=OC，∠AOD=∠BOC；
∴△AOD≌△COB（SAS）；①
同理可得出△AOB≌△COD（SAS）；②
∵BC=AD，CD=AB，BD=BD；
∴△ABD≌△CDB（SSS）；③
同理可得：△ACD≌△CAB（SSS）．④
因此本题共有4对全等三角形，故选C．
　
4．解：A、当AE=CF无法得出△ABE≌△CDF，故此选项符合题意；
B、当BE=FD，
∵平行四边形ABCD中，
∴AB=CD，∠ABE=∠CDF，
在△ABE和△CDF中
，
∴△ABE≌△CDF（SAS），故此选项错误；
C、当BF=ED，
∴BE=DF，
∵平行四边形ABCD中，
∴AB=CD，∠ABE=∠CDF，
在△ABE和△CDF中
，
∴△ABE≌△CDF（SAS），故此选项错误；
D、当∠1=∠2，
∵平行四边形ABCD中，
∴AB=CD，∠ABE=∠CDF，
在△ABE和△CDF中
，
∴△ABE≌△CDF（ASA），故此选项错误；
故选：A．
　
5．解：∵四边形ABCD是平行四边形，
∴OC=AC=5，OB=BD=6，
在△OBC中，6﹣5＜m＜6+5，
∴1＜m＜11；
故选：C．
　
二．填空题（共4小题）
6．解：如图：∵矩形的周长为40cm，被两条对角线分成的相邻两个三角形的周长的差为8cm，
∴AB+BC=20cm，当C△AOB﹣C△OBC=8，AO=CO=BO=DO，
∴BC﹣AB=8，
∴BC=AB+8，则AB+AB+8=20，
解得：AB=6，
∴BC=14，
故较长边为：14cm．
故答案为：14cm．
　
7．
解：根据平行四边形的性质可得平行四边形被分成5组全等的三角形，
故S阴影=SABCD=12．
故答案为：12．
　
8．解：因为平行四边形的对角线互相平分，
所以OA=OC，
又因为OE⊥AC交AD于点E，
所以AE=CE，
由平行四边形ABCD的周长为16cm，
可得AD+DC=8cm，
△DCE的周长=DE+CE+DC=AD+DC=8cm．
故答案为8cm．
　
9．解：∵四边形ABCD是平行四边形，
∴O1A=O1C1，O1B=O1O，
∴SAO1B=S△ABC1=S?ABCD=4cm2，
∵四边形ABC1O1是平行四边形，O1A=O1B，
∴四边形ABC1O是菱形，
∴AC1=2O2A，O1B=2O1O2=2O2B，AC1⊥BO1，
∴平行四边形ABC1O1的面积是AC1×BO1=×2AO2×BO1=2×AO2×BO1=2×4cm2=8cm2，21世纪教育网版权所有
∴△ABO2的面积=2cm2，
同理平行四边形ABC2O2的面积是4cm2，
平行四边形ABC3O3的面积是2cm2，
平行四边形ABC4O4的面积是1cm2，
平行四边形ABC5D5的面积是cm2，
…以此类推?AOnCn+1B的面积为：或
故答案为：8；；或．
　
三．解答题（共7小题）
10．解：∵四边形ABCD是平行四边形，且周长为22cm，
∴AD+AB=11cm，OB=OD，
∵△A0D的周长比△ABO的周长小3cm，
∴（OA+0B+AB）﹣（OA+OD+AD）=AB﹣AD=3cm，
∴AD=4cm，AB=7cm．
　
11．证明：∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD，
∵AM=CN，∴OM=ON，
在△BOM和△DON中，，
∴△BOM≌△DON（SAS），
∴∠OBM=∠ODN，
∴BM∥DN．
　
12．（1）解：如图所示：
（2）证明：∵四边形ABCD是平行四边形，对角线AC、BD交于点O，
∴OB=OD，OA=OC．
又∵E，F分别是OA、OC的中点，
∴OE=OA，OF=OC，
∴OE=OF．
∵在△BEO与△DFO中，，
∴△BEO≌△DFO（SAS），
∴BE=DF．
　
13．证明：∵四边形ABCD是平行四边形，
∴AB∥CD，OA=OC，
∴∠OAE=∠OCF，
在△OAE和△OCF中，
，
∴△AOE≌△COF（ASA），
∴AE=CF．
　
14．解：（1）无数；
（2）作图的时候要首先找到对角线的交点，只要过对角线的交点，任画一条直线即可．如图有：AE=BE=DF=CF，AM=CN．21教育网
（3）这两条直线过平行四边形的对称中心（或对角线的交点）．
　
15．解：如图所示：EF即为所求．
理由过□ABCD两对角线的交点O和点P画直线EF，分别交AD，BC于E，F，
∵S△ACD=S△ACB，S△AOE=S△COF，
∴S□EABF=S□DEFC．
　
16．解：（1）∵BC⊥AC，AB=8，∠ABC=30°，
∴AC=AB=4，
在Rt△ABC中，BC===4，
∵四边形ABCD是平行四边形，
∴AD=BC=4，
设AC与BD相交于O点，
∴OD=BD，OA=AC=2，
在Rt△AOD中，OD==2，
∴BD=2OD=4；
（2）S?ABCD=BC?AC=4×4=16．