4.4平行四边形的判定（1）同步练习

登陆21世纪教育 助您教考全无忧
浙教版八下数学4.4平行四边形的判定（1）同步练习
　
一．选择题（共4小题）
1．下列条件中，不能判定四边形是平行四边形的是（　　）
A．两组对边分别平行
B．一组对边平行，另一组对边相等
C．两组对边分别相等
D．一组对边平行且相等
2．如图，在平行四边形ABCD中，E、F分别为AB、CD的中点，连接DE、EF、FB，则图中共有平行四边形的个数（平行四边形ABCD除外）为（　　）
A．1个 B．2个 C．3个 D．4个
3．下面给出的是四边形ABCD中∠A、∠B、∠C、∠D的度数比，其中能判断出四边形是平行四边形的是（　　）21世纪教育网版权所有
A．4：3：2：1 B．3：2：3：2
C．3：3：2：2 D．3：2：2：1
4．四边形ABCD中，对角线AC、BD相交于点O，给出下列四个条件：①AD∥BC；②AD=BC；③OA=OC；④OB=OD，从中任选两个条件，能使四边形ABCD为平行四边形的选法有（　　）21教育网
A．6种 B．5种 C．4种 D．3种
　
二．填空题（共5小题）
5．在四边形ABCD中，AB=5，BC=8，当CD=　　，AD=　　时，四边形ABCD是平行四边形．21·cn·jy·com
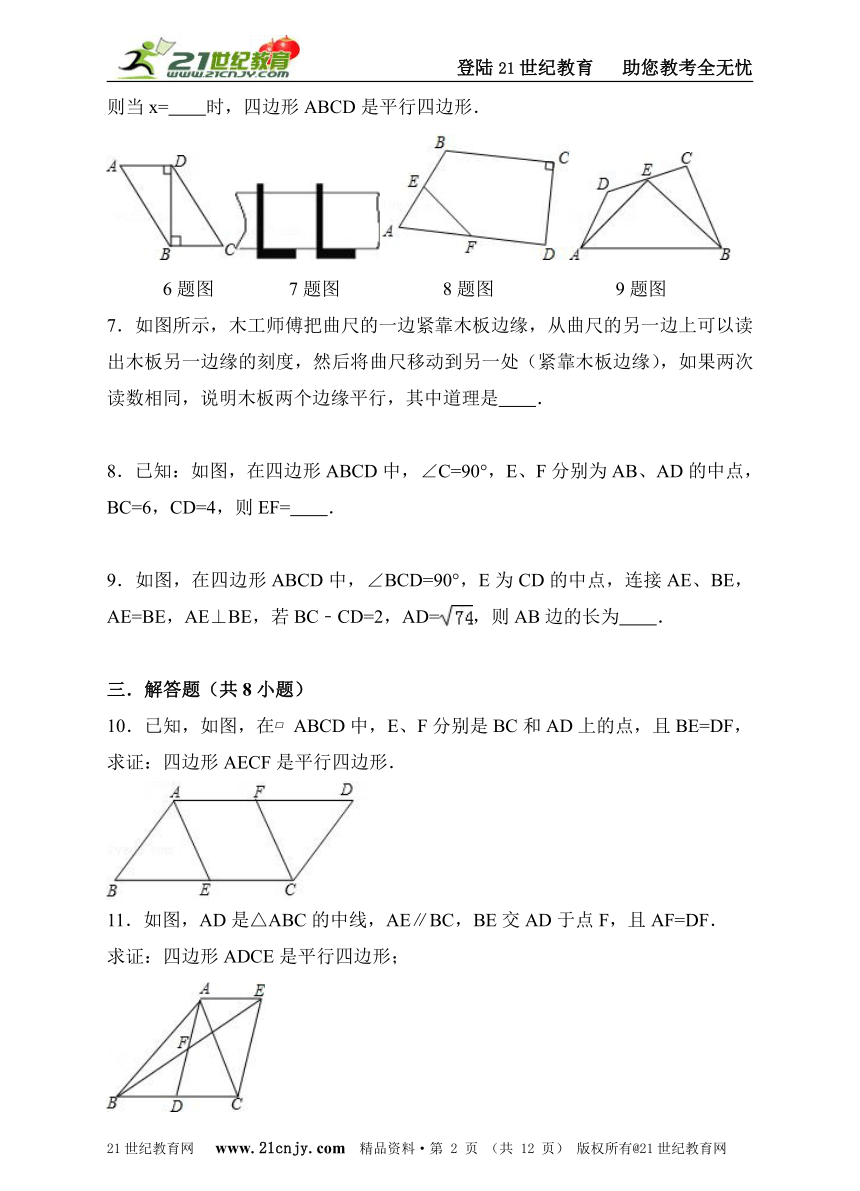
6．如图，四边形ABCD中，对角线BD⊥AD，BD⊥BC，AD=11﹣x，BC=x﹣5，则当x=　　时，四边形ABCD是平行四边形．www.21-cn-jy.com
6题图 7题图 8题图 9题图
7．如图所示，木工师傅把曲尺的一边紧靠木板边缘，从曲尺的另一边上可以读出木板另一边缘的刻度，然后将曲尺移动到另一处（紧靠木板边缘），如果两次读数相同，说明木板两个边缘平行，其中道理是　　．【来源：21·世纪·教育·网】
8．已知：如图，在四边形ABCD中，∠C=90°，E、F分别为AB、AD的中点，BC=6，CD=4，则EF=　　．21·世纪*教育网
9．如图，在四边形ABCD中，∠BCD=90°，E为CD的中点，连接AE、BE，AE=BE，AE⊥BE，若BC﹣CD=2，AD=，则AB边的长为　　．
三．解答题（共8小题）
10．已知，如图，在 ABCD中，E、F分别是BC和AD上的点，且BE=DF，
求证：四边形AECF是平行四边形．
11．如图，AD是△ABC的中线，AE∥BC，BE交AD于点F，且AF=DF．
求证：四边形ADCE是平行四边形；
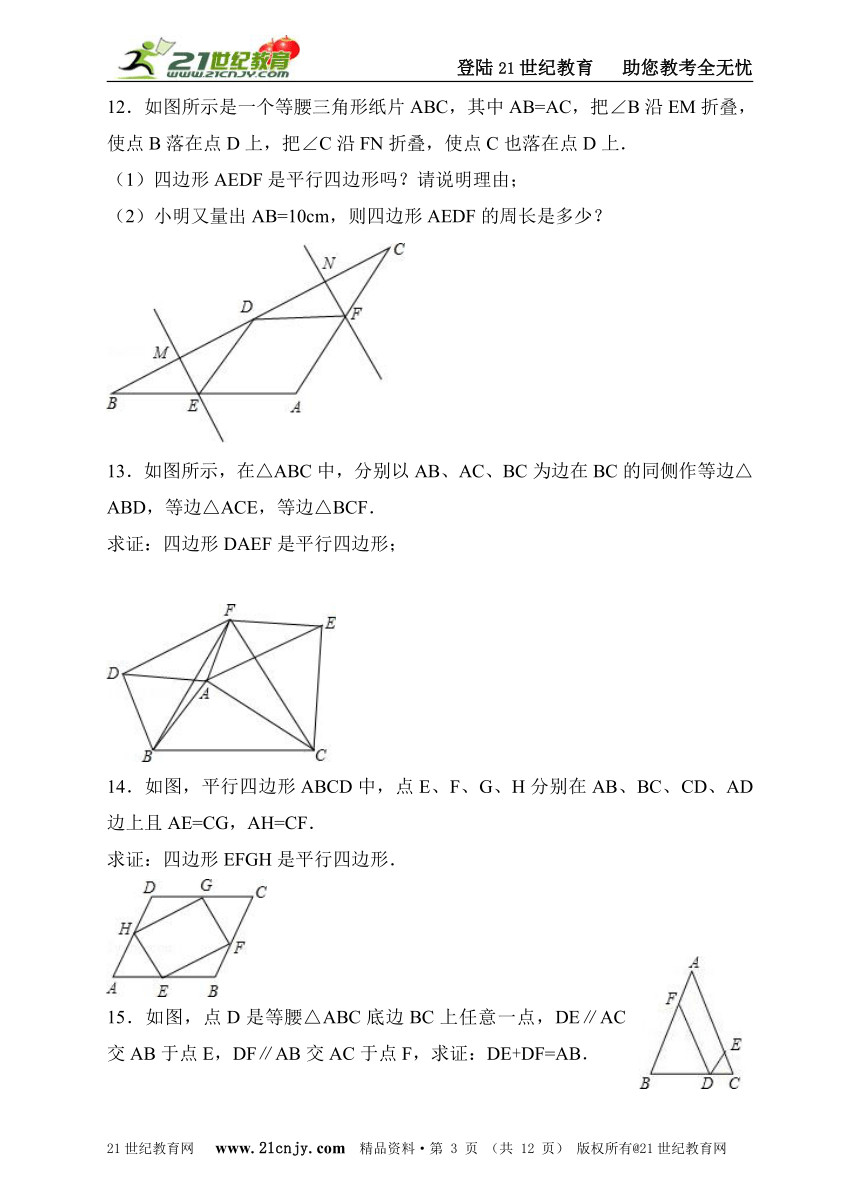
12．如图所示是一个等腰三角形纸片ABC，其中AB=AC，把∠B沿EM折叠，使点B落在点D上，把∠C沿FN折叠，使点C也落在点D上．
（1）四边形AEDF是平行四边形吗？请说明理由；
（2）小明又量出AB=10cm，则四边形AEDF的周长是多少？
13．如图所示，在△ABC中，分别以AB、AC、BC为边在BC的同侧作等边△ABD，等边△ACE，等边△BCF．www-2-1-cnjy-com
求证：四边形DAEF是平行四边形；
14．如图，平行四边形ABCD中，点E、F、G、H分别在AB、BC、CD、AD边上且AE=CG，AH=CF．2-1-c-n-j-y
求证：四边形EFGH是平行四边形．
15．如图，点D是等腰△ABC底边BC上任意一点，DE∥AC交AB于点E，DF∥AB交AC于点F，求证：DE+DF=AB．
16．如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE，已知：∠BAC=30°，EF⊥AB，垂足为F，连接DF．
（1）试说明AC=EF；
（2）求证：四边形ADFE是平行四边形．
17．如图所示，在四边形ABCD中，AD∥BC，BC=6厘米，AD=9厘米，P，Q分别从点A，C同时出发，P以1厘米/秒的速度由A向D运动，Q以2厘米/秒的速度由C向B运动．2·1·c·n·j·y
（1）几秒时四边形ABQP为平行四边形？
（2）几秒时直线PQ将四边形ABCD截出一个平行四边形？
　
浙教版八下数学4.4平行四边形的判定（1）
参考答案与试题解析
　
一．选择题（共4小题）
1．解：∵两组对边分别平行的四边形是平行四边形，
∴A正确；
∵一组对边平行，另一组对边相等的四边形是等腰梯形，不一定是平行四边形，
∴B不正确；
∵两组对边分别相等的四边形是平行四边形，
∴C正确；
∵一组对边平行且相等的四边形是平行四边形，
∴D正确；
故选：B．
　
2．解：∵四边形ABCD是平行四边形
∴AB∥CD，AB=CD
∵E，F分别AB，CD的中点
∴AE=EB=DF=FC
∴四边形AEFD是平行四边形，四边形EFCB是平行四边形，四边形BEDF是平行四边形．
∴平行四边形的个数共有3个（平行四边形ABCD除外）．
故选：C．
　
3．解：根据平行四边形的两组对角分别相等，可知B正确．
故选：B．
　
4．解：①②组合可根据一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形；
③④组合可根据对角线互相平分的四边形是平行四边形判定出四边形ABCD为平行四边形；
①③可证明△ADO≌△CBO，进而得到AD=CB，可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形；21cnjy.com
①④可证明△ADO≌△CBO，进而得到AD=CB，可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形；21*cnjy*com
∴有4种可能使四边形ABCD为平行四边形．
故选：C．
　
二．填空题（共5小题）
5．解：根据平行四边形的判定：两组对边分别相等的四边形是平行四边形．可得，CD=5，AD=8．
故答案为：5、8．
　
6．解：∵BD⊥AD，BD⊥BC，
∴AD∥BC，
只要AD=BC，四边形ABCD是平行四边形．
AD=BC
11﹣x=x﹣5
x=8．
故答案为：8．
　
7．解：根据题意得：
AB=CD，AB∥CD，
∴四边形ABCD是平行四边形，
∴AD∥BC．
故答案为：平行四边形的对边平行．
　
8．解：如图，连接BD，
∵∠C=90°，BC=6，CD=4，
∴BD===2，
∵E、F分别为AB、AD的中点，
∴EF是△ABD的中位线，
∴EF=BD=×2=．
故答案为：．
　
9．解：过A作AF⊥CD于点F
∵∠F=∠AEB=∠C=90°，
∴∠AEF+∠FAD=90°，∠AEF+∠CEB=90°，
∴∠FAE=∠CEB，
在△AFE和△ECB中，
，
∴△AFE≌△ECB
∴AF=CE，EF=BC
∵E是CD中点，
∴DE=EC
∵BC﹣CD=2，
∴BC=CD+2
设CE=x，则AF=DE=x，CD=2x，EF=BC=2x+2
DF=EF﹣DE=2x+2﹣x=x+2
在Rt△ADF中，x2+（x+2）2=（）2
∴x=5
在Rt△AEF中，AE==13，
∴AB=AE=13，
故答案为13
　
三．解答题（共8小题）
10．证明：∵四边形ABCD平行四边形
∴AD=BC．
又∵BE=DF，
∴AF=EC．
又∵AF∥EC，
∴四边形AECF是平行四边形．
　
11．证明：∵AD是△ABC的中线，
∴BD=CD，
∵AE∥BC，
∴∠AEF=∠DBF，
在△AFE和△DFB中，
，
∴△AFE≌△DFB（AAS），
∴AE=BD，
∴AE=CD，
∵AE∥BC，
∴四边形ADCE是平行四边形；
　
12．解：（1）四边形AEDF是平行四边形；
∵AB=AC，
∴∠B=∠C，
根据折叠的性质，∠B=∠BDE，∠C=∠CDF，
∴∠B=∠CDF，∠C=∠BDE，
∴DF∥AB，DE∥AC，
∴四边形AEDF是平行四边形；
（2）根据折叠的性质，BE=DE，CF=DF，
∴AE+ED=AB，DF+AF=AC，
∵AB=AC，AB=10cm，
∴四边形AEDF的周长=AB+AC=2AB=20cm．
　
13．证明：∵△ABD、△BCE、△ACE是等边三角形，
∴AC=CE=AE，AB=AD=BD，BC=CF=BF，∠BCF=∠ACE=60°，
∴∠BCA=∠FCE=60°﹣∠ACF，
在△BCA和△FCE中，
，
∴△BCA≌△FCE（SAS），
∴EF=BA=AD，
同理DF=AC=AE，
∴四边形DAEF是平行四边形；
　
14．证明：在平行四边形ABCD中，∠A=∠C（平行四边形的对边相等）；
又∵AE=CG，AH=CF（已知），
∴△AEH≌△CGF（SAS），
∴EH=GF（全等三角形的对应边相等）；
在平行四边形ABCD中，AB=CD，AD=BC（平行四边形的对边相等），
∴AB﹣AE=CD﹣CG，AD﹣AH=BC﹣CF，
即BE=DG，DH=BF．
又∵在平行四边形ABCD中，∠B=∠D，
∴△BEF≌△DGH；
∴GH=EF（全等三角形的对应边相等）；
∴四边形EFGH是平行四边形（两组对边分别相等的四边形是平行四边形）．
　
15．证明：如图∵DE∥AB，DF∥AC，
∴四边形AEDF是平行四边形，
∴DF=AE，
又∵DE∥AB，
∴∠B=∠EDC，
又∵AB=AC，
∴∠B=∠C，
∴∠C=∠EDC，
∴DE=CE，
∴DF+DE=AE+CE=AC=AB．
　
16．证明：（1）∵Rt△ABC中，∠BAC=30°，
∴AB=2BC，
又∵△ABE是等边三角形，EF⊥AB，
∴AB=2AF
∴AF=BC，
在Rt△AFE和Rt△BCA中，
，
∴Rt△AFE≌Rt△BCA（HL），
∴AC=EF；
（2）∵△ACD是等边三角形，
∴∠DAC=60°，AC=AD，
∴∠DAB=∠DAC+∠BAC=90°
又∵EF⊥AB，
∴EF∥AD，
∵AC=EF，AC=AD，
∴EF=AD，
∴四边形ADFE是平行四边形．
　
17．解：（1）设t秒后四边形ABQP是平行四边形；
根据题意得：AP=tcm，CQ=2tcm，
则BQ=（6﹣2t）cm；
∵AD∥BC，
∴当AP=BQ时，四边形ABQP是平行四边形，
∴t=6﹣2t，
解得：t=2，
即2秒时四边形ABQP是构成平行四边形；
（2）由（1）知，2秒时四边形ABQP是平行四边形，
根据题意得：AP=xcm，CQ=2xcm，
则PD=（9﹣x）cm；
∵AD∥BC，
∴当AP=BQ时，四边形DCQP是平行四边形，
∴2x=9﹣x，
解得：x=3，
因此2或3秒时直线PQ将四边形ABCD截出一个平行四边形．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网 www.21cnjy.com 精品资料·第 1 页 （共 1 页） 版权所有@21世纪教育网