4.1.1多边形 （1）同步练习

多边形
班级：___________姓名：___________得分：__________
选择题
1、已知四边形ABCD中，∠A与∠B互补，∠D＝70°，则∠C的度数为(　 　)
A．70°　　　　　 B．90° C．110° D．140°
2.一个多边形的每个内角均为 120?，则这个多边形是( )
A. 四边形 B. 五边形 C. 六边形 D. 七边形
3．在四边形的四个内角中，直角最多可以有( 　)
A．1个 B．2个 C．3个 D．4个
4.
如图，在四边形 ABCD 中，AB = AC = AD = BD，则 BCD 等于 (
)
A. 100?
B. 120?
C. 135?
D. 150?
二、填空题
1、在四边形ABCD中，∠A与∠C互补，∠B＝85°，则∠D＝____．
2、
正五边形的一个内角是
________度．
3、已知四边形各内角的度数的比为1∶2∶3∶4，则各内角的度数分别为______
如图所示，已知四边形ABCD中，∠A＝95°，∠D＝100°，外角∠ABE＝70°，则∠ABC＝____，∠C＝____．21教育网
三、解答题
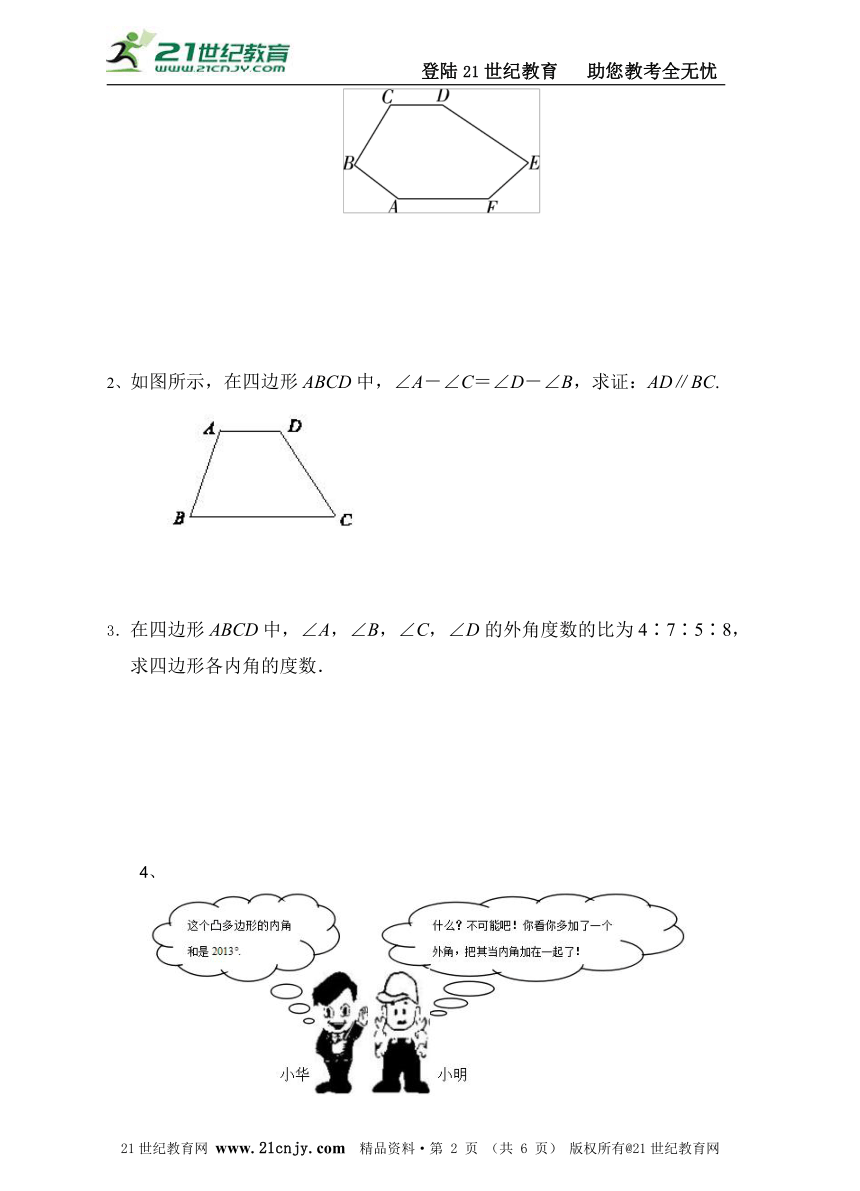
1、如图，CD∥AF，∠CDE＝∠BAF，AB⊥BC，∠C＝120°，∠E＝80°，试求∠F的度数．21cnjy.com
2、如图所示，在四边形ABCD中，∠A－∠C＝∠D－∠B，求证：AD∥BC.
3．在四边形ABCD中，∠A，∠B，∠C，∠D的外角度数的比为4∶7∶5∶8，求四边形各内角的度数．2·1·c·n·j·y

4、
（1）内角和为2013°，小明为什么说不可能？
（2）小华求的是几边形的内角和？
（3）错把外角当内角的那个外角的度数你能求出吗？是多少度呢？
参考答案
选择题、
1.C
【解析】 ∠C＝360°－(∠A＋∠B＋∠D)＝360°－(180°＋70°)＝110°.选C.
2． C
【解析】主要考查的是运用多边形内角和与外角和公式计算多边形的边数．多边形的每个内角均为 120?，得出每个外角均为 60?．外角和为 360?，) 这个多边形的边数为 360? 60? = 6．21·cn·jy·com
D
【解析】四边形内角和为360°，所以直角90°可以有四个
B
【解析】4. 因为 AB = AC = AD = BD，所以 ABD 是正三角形，ABC = ACB，ACD = ADC．www.21-cn-jy.com
所以 BAD = 60?．
因为 BAD + ADC + BCD + ABC = 360?，所以 ADC + BCD + ABC = 300?，
所以 2BCD = 300?，
所以 BCD = 150?．
二、填空题
1、95°
【解析】∵∠A＋∠C＝180°，∠B＝85°，∴∠D＝360°－∠A－∠C－∠B＝360°－180°－85°＝95°.【来源：21·世纪·教育·网】
2、108°
【解析】五边形的内角和为540°，所以正五边形一个内角为108°
3、36°，72°，108°，144°．
【解析】 设四个角分别为x，2x，3x，4x，
则x＋2x＋3x＋4x＝360°，解得x＝36°，
∴2x＝72°，3x＝108°，4x＝144°.
4、110°；55°
【解析】∠ABC＝180°－∠ABE＝180°－70°＝110°，∠C＝360°－∠A－∠ABC－∠D＝360°－95°－110°－100°＝55°.21·世纪*教育网
三、解答题
1、解：如图，连结AD，在四边形ABCD中，∠BAD＋∠ADC＋∠B＋∠C＝360°.
∵AB⊥BC，∴∠B＝90°.
[
第8题答图
又∵∠C＝120°，∴∠BAD＋∠ADC＝150°.
∵CD∥AF，∴∠CDA＝∠DAF.
又∵∠CDE＝∠BAF，∴∠EDA＝∠BAD.
在四边形ADEF中，
∠DAF＋∠EDA＋∠F＋∠E＝360°，
∴∠F＋∠E＝360°(∠ADC＋∠BAD)＝210°.
又∵∠E＝80°，∴∠F＝130°.
2、证明：∵∠A＋∠B＋∠C＋∠D＝360°，
又∠A－∠C＝∠D－∠B，
∴∠A＋∠B＝∠C＋∠D，
∴2∠A＋2∠B＝360°，∴∠A＋∠B＝180°，[
∴AD∥BC.

3、解：∵四边形的外角和是360°，
设∠A，∠B，∠C，∠D的外角度数分别为4x，7x，5x，8x，则4x＋7x＋5x＋8x＝360°，21世纪教育网版权所有
∴x＝15°，∴4x＝60°，7x＝105°，5x＝75°，8x＝120°，
故四边形各内角的度数分别为120°，75°，105°，60°
4、解：（1）因为内角和是180的倍数，而2013°不是180°的倍数，所以说不可能.
（2）设多边形的边数为n，则有(n－2)?180°<2013°，解得n<，故是十三边形.
（3）2013°－1980°＝33°，所以这个外角为33°.