4.2.1平行四边形的判定定理(1) 同步练习
文档属性
| 名称 | 4.2.1平行四边形的判定定理(1) 同步练习 |

|
|
| 格式 | doc | ||
| 文件大小 | 256.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-14 00:00:00 | ||
图片预览

文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
平行四边形的判定定理-----第一课时
班级:___________姓名:___________得分:__________
1、选择题
1、如图,在□ABCD中,AB= ( http: / / www.21cnjy.com )4,∠BAD的平分线与BC的延长线相交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的长为( )
A.2 B.4 C.4 D.8
( http: / / www.21cnjy.com )
2、已知四边形ABCD,有下列条件:①AB ( http: / / www.21cnjy.com )∥CD;②BC∥AD;③AB=CD;④BC=AD;⑤∠A=∠C;⑥∠B=∠D. 任取其中两个,可以得出“四边形ABCD是平行四边形”这一结论的情况有( )21世纪教育网版权所有
A. 4种 B. 9种 C. 13种 D. 15种
3、已知四边形ABCD的四条边长分别为 ( http: / / www.21cnjy.com )a,b,c,d,其中a,b为对边,且a2+b2+c2+d2=2ab+2cd,则此四边形一定是( )21·cn·jy·com
A.任意四边形
B.对角线相等的四边形
C.对角线互相垂直且相等的四边形
D.平行四边形
2、填空题
1、如图, ABCD的对角线AC,BD相交于点O,点E是AD的中点,△BCD的周长为8 cm,则△DEO的周长是 cm.www.21-cn-jy.com
( http: / / www.21cnjy.com )
2、如图,□ABCD与□DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为 ___________.2·1·c·n·j·y
( http: / / www.21cnjy.com )
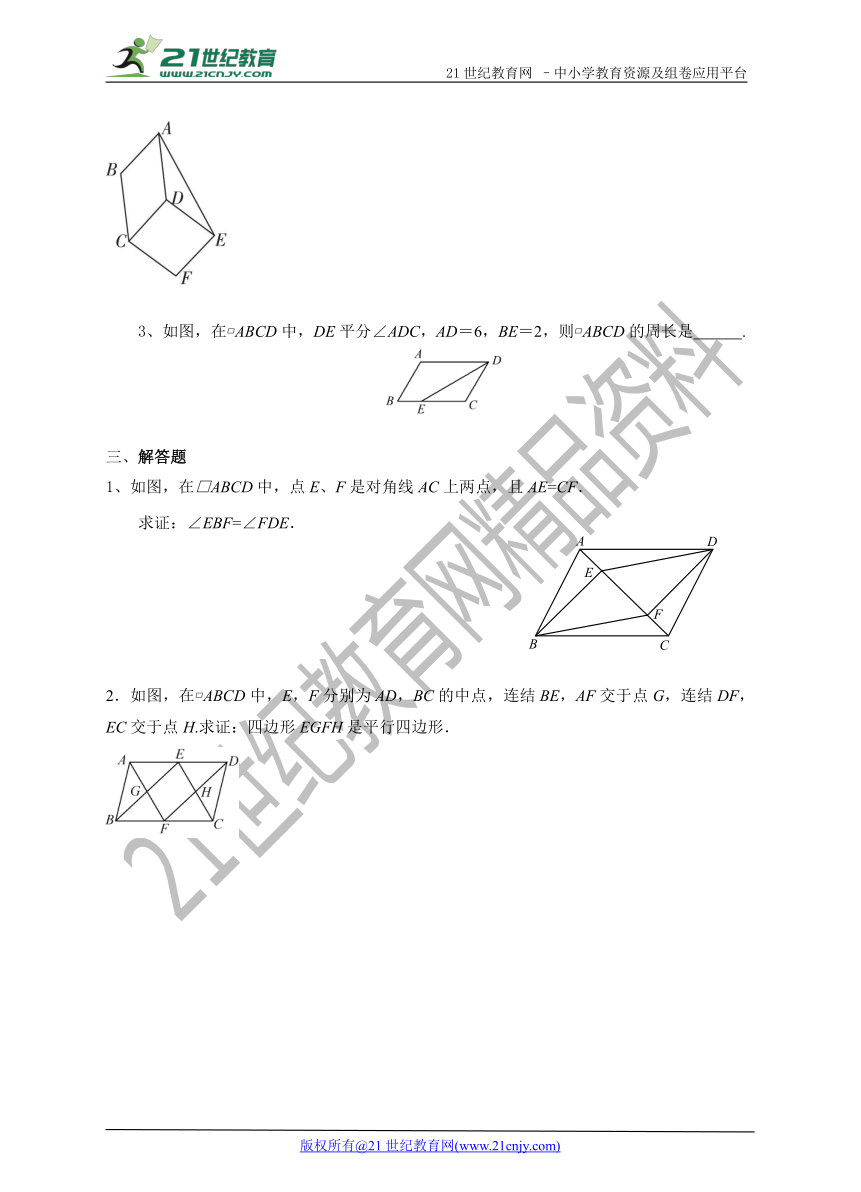
3、如图,在 ABCD中,DE平分∠ADC,AD=6,BE=2,则 ABCD的周长是 .
三、解答题
1、如图,在□ABCD中,点E、F是对角线AC上两点,且AE=CF.
求证:∠EBF=∠FDE.
2.如图,在 ABCD中,E,F分别为AD,BC的中点,连结BE,AF交于点G,连结DF,EC交于点H.求证:四边形EGFH是平行四边形.21cnjy.com
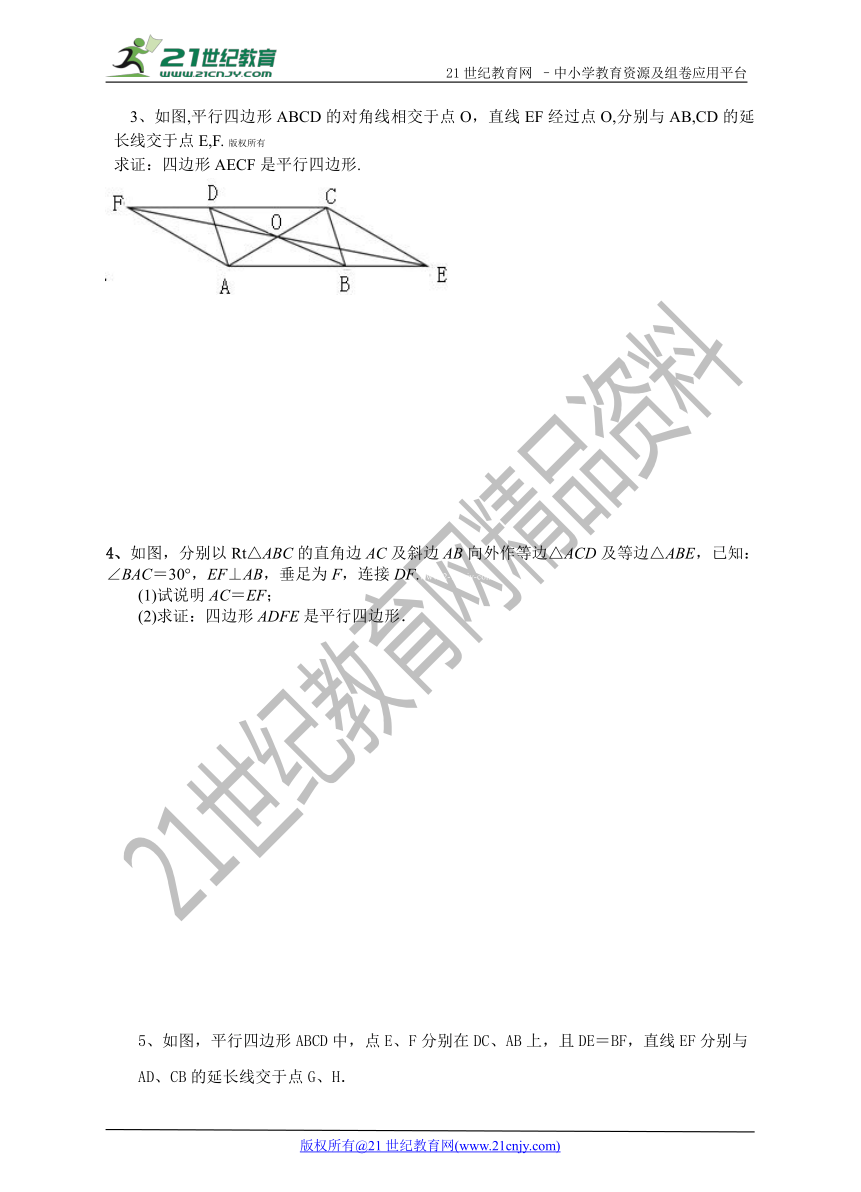
3、如图,平行四边形ABCD的对角线相交于点O,直线EF经过点O,分别与AB,CD的延长线交于点E,F. 版权所有【来源:21·世纪·教育·网】
求证:四边形AECF是平行四边形.
4、如图,分别以Rt△AB ( http: / / www.21cnjy.com )C的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF.www-2-1-cnjy-com
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
5、如图,平行四边形ABCD中,点E、F分别在DC、AB上,且DE=BF,直线EF分别与AD、CB的延长线交于点G、H.2-1-c-n-j-y
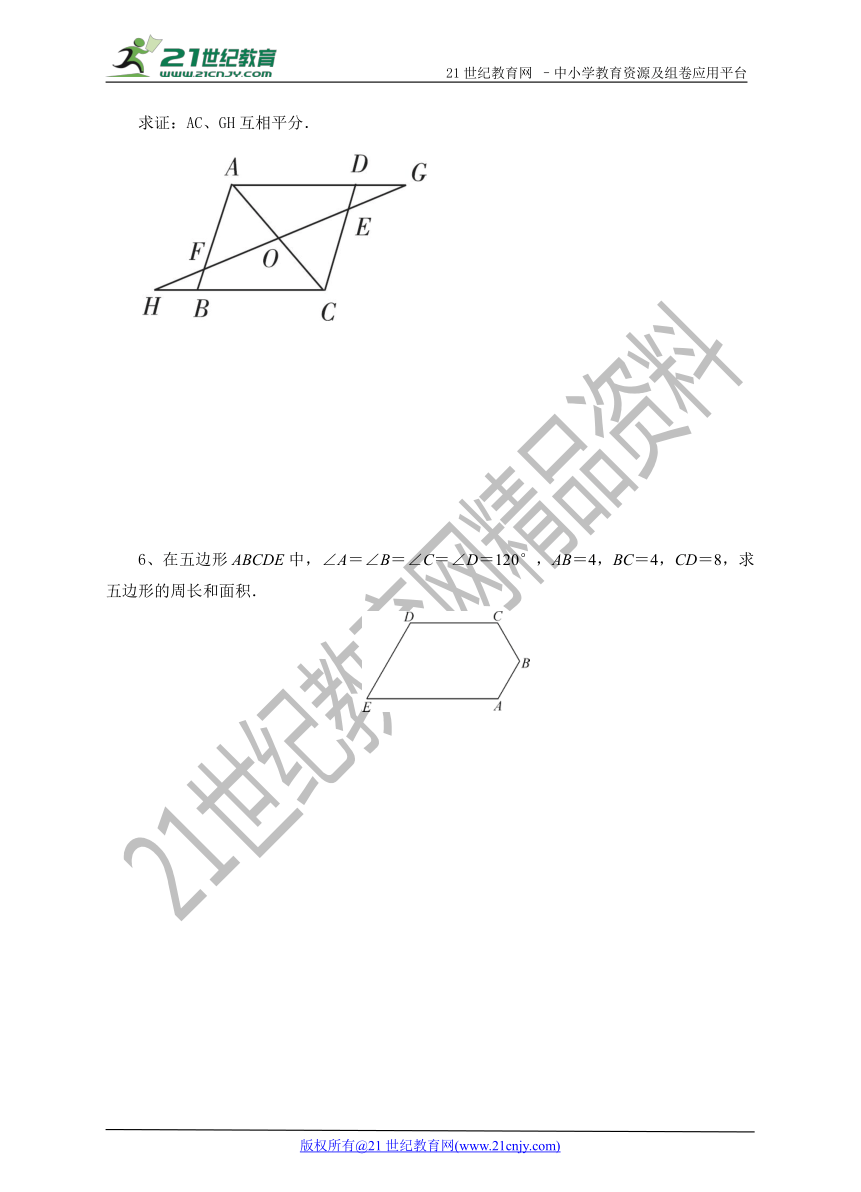
求证:AC、GH互相平分.
( http: / / www.21cnjy.com )
6、在五边形ABCDE中,∠A=∠B=∠C=∠D=120°,AB=4,BC=4,CD=8,求五边形的周长和面积.21*cnjy*com
参考答案
一、选择题
1、B
【解析】
通过△ADF≌△ECF可说明AE=2A ( http: / / www.21cnjy.com )F.由DC∥AB,AF是∠BAD的平分线,可推导AD=FD,在Rt△DGF中可计算GF,根据AE=2AF=4GF可求解.21·世纪*教育网
2、B
【解析】 利用“两组对边分别平行的 ( http: / / www.21cnjy.com )四边形是平行四边形”的条件有①②;利用“两组对边分别相等的四边形是平行四边形”的条件有③④;利用“一组对边平行且相等的四边形是平行四边形”的条件有①③,②④;利用“两组对角相等的四边形是平行四边形”(可利用四边形的内角和定理证明同旁内角互补,转化为两组对边分别平行)的条件有:⑤⑥,①⑤,①⑥,②⑤,②⑥.【来源:21cnj*y.co*m】
3、D
【解析】由题意可得(a-b)2+(c-d)2=0,
∴a=b,c=d,∴四边形ABCD为平行四边形.
二、填空题
1、4.
【解析】在 ABCD中,OB=OD ( http: / / www.21cnjy.com ),OA=OC, 又∵点E是AD的中点,∴OE是△ACD的中位线,∴OE=CD.∵△BCD的周长为8 cm,即BC+CD+BD=8 cm.又∵DE=AD=BC,∴△DEO的周长=DE+OE+OD=BC+CD+BD=(BC+CD+BD)=×8=4(cm).
答案:4
2、25°
【解析】
两个平行四边形的周长相等,且有公共边CD,则 ( http: / / www.21cnjy.com )有AD=DE,即△ADE为等腰三角形,∠ADE=∠BCF=60°+70°=130°,∴∠DAE=25°.21教育网
3、 20.
【解析】
在 ABCD中,BC=AD=6,∵BE=2,
∴CE=4.∵AD∥BC,∴∠ADE=∠CED.
∵DE平分∠ADC,∴∠ADE=∠CDE.
∴∠CED=∠CDE,
∴CD=CE=4.∴ ABCD的周长是(6+4)×2=20.
三、解答题
1、证明:连接BD交AC于O点
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
又∵AE=CF
∴OE=OF
∴四边形BEDF是平行四边形
∴∠EBF=∠EDF
2、【解】 ∵E,F分别是AD,BC的中点,
∴AE=DE=AD,BF=CF=BC.
又∵四边形ABCD是平行四边形,
∴AD平行且等于BC.∴AE平行且等于FC,DE平行且等于BF,
∴四边形AECF和四边形BFDE都是平行四边形,
∴AF∥EC,BE∥DF,即FG∥EH,EG∥FH,
∴四边形EGFH是平行四边形.
3、【解】
证明:∵四边形ABCD是平行四边形,∴OD=OB,OA=OC
∴∠DFO=∠BEO, ∠FDO=∠EBO
∴△FDO≌△EBO
∴OF=OE
∴四边形AECF是平行四边形
4、(1)∵△ABE是等边三角形,EF⊥AB,
∴∠AEF=∠AEB=30°,AE=AB,∠EFA=90°.
又∵∠ACB=90°,∠BAC=30°,
∴∠EFA=∠ACB,∠AEF=∠BAC.
∴△ACB≌△EFA.
∴AC=EF.
(2)证明:∵△ACD是等边三角形,
∴AC=AD,∠DAC=60°.
由(1)的结论得AC=EF,∴AD=EF.
又∵∠BAC=30°,∴∠FAD=∠BAC+∠DAC=90°.
又∵∠EFA=90°,∴EF∥AD.
又∵EF=AD,
∴四边形ADFE是平行四边形.
5、证明:□ABCD中,AD∥BC,AD=BC,∠ADC=∠ABC.
∵AD∥BC,∴∠G=∠H.
∵∠ADC=∠ABC,∴∠GDC=∠HBA.
在△GDE和△HBF中,∠G=∠H.∠GDC=∠HBA,DE=BF.
∴△GDE≌△HBF,∴GD=BH.∵AD=BC,∴AC=GH.
∵平行四边形ABCD中,AD∥BC,∴∠DAC=∠BCA.
在△AGO和△CHO中,∠G=∠H,∠DAC=∠BCA,AG=CH.
∴△AGO≌△CHO,∴OG=OH,OA=OC.∴AC、GH互相平分.
6、 如解图,连结AC,延长AB和DC交于点F,过点B作BM⊥CF于点M.
(第14题解)
∵∠ABC=∠DCB=120°,
∴∠FBC=∠FCB=60°,
∴△CBF是等边三角形,
∴∠F=60°,CF=BF=BC=4.
∵BM⊥CF,
∴CM=FM=2.
∴由勾股定理,得BM=2.
∵∠EAB=120°,∠F=60°,
∴∠EAB+∠F=180°,
∴AE∥DF.
同理,DE∥AF.
∴四边形EAFD是平行四边形.
∴DE=AF=AB+BF=8,
AE=DF=CD+CF=12.
∴五边形的周长=DE+DC+BC+AB+AE=36.
∵∠ABC=120°,BC=AB=4,
∴∠BCA=∠BAC=30°,
∴∠ACF=180°-(120°-30°)=90°.
在Rt△ACF中,由勾股定理,得AC=4,
∴五边形的面积=S DEAF-S△CBF=AE·AC-CF·BM=12×4-×4×2=44.
答:五边形的周长是36,面积是44.
D
A
E
F
B
C
C
A
B
D
E
F
O
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
平行四边形的判定定理-----第一课时
班级:___________姓名:___________得分:__________
1、选择题
1、如图,在□ABCD中,AB= ( http: / / www.21cnjy.com )4,∠BAD的平分线与BC的延长线相交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的长为( )
A.2 B.4 C.4 D.8
( http: / / www.21cnjy.com )
2、已知四边形ABCD,有下列条件:①AB ( http: / / www.21cnjy.com )∥CD;②BC∥AD;③AB=CD;④BC=AD;⑤∠A=∠C;⑥∠B=∠D. 任取其中两个,可以得出“四边形ABCD是平行四边形”这一结论的情况有( )21世纪教育网版权所有
A. 4种 B. 9种 C. 13种 D. 15种
3、已知四边形ABCD的四条边长分别为 ( http: / / www.21cnjy.com )a,b,c,d,其中a,b为对边,且a2+b2+c2+d2=2ab+2cd,则此四边形一定是( )21·cn·jy·com
A.任意四边形
B.对角线相等的四边形
C.对角线互相垂直且相等的四边形
D.平行四边形
2、填空题
1、如图, ABCD的对角线AC,BD相交于点O,点E是AD的中点,△BCD的周长为8 cm,则△DEO的周长是 cm.www.21-cn-jy.com
( http: / / www.21cnjy.com )
2、如图,□ABCD与□DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为 ___________.2·1·c·n·j·y
( http: / / www.21cnjy.com )
3、如图,在 ABCD中,DE平分∠ADC,AD=6,BE=2,则 ABCD的周长是 .
三、解答题
1、如图,在□ABCD中,点E、F是对角线AC上两点,且AE=CF.
求证:∠EBF=∠FDE.
2.如图,在 ABCD中,E,F分别为AD,BC的中点,连结BE,AF交于点G,连结DF,EC交于点H.求证:四边形EGFH是平行四边形.21cnjy.com
3、如图,平行四边形ABCD的对角线相交于点O,直线EF经过点O,分别与AB,CD的延长线交于点E,F. 版权所有【来源:21·世纪·教育·网】
求证:四边形AECF是平行四边形.
4、如图,分别以Rt△AB ( http: / / www.21cnjy.com )C的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF.www-2-1-cnjy-com
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
5、如图,平行四边形ABCD中,点E、F分别在DC、AB上,且DE=BF,直线EF分别与AD、CB的延长线交于点G、H.2-1-c-n-j-y
求证:AC、GH互相平分.
( http: / / www.21cnjy.com )
6、在五边形ABCDE中,∠A=∠B=∠C=∠D=120°,AB=4,BC=4,CD=8,求五边形的周长和面积.21*cnjy*com
参考答案
一、选择题
1、B
【解析】
通过△ADF≌△ECF可说明AE=2A ( http: / / www.21cnjy.com )F.由DC∥AB,AF是∠BAD的平分线,可推导AD=FD,在Rt△DGF中可计算GF,根据AE=2AF=4GF可求解.21·世纪*教育网
2、B
【解析】 利用“两组对边分别平行的 ( http: / / www.21cnjy.com )四边形是平行四边形”的条件有①②;利用“两组对边分别相等的四边形是平行四边形”的条件有③④;利用“一组对边平行且相等的四边形是平行四边形”的条件有①③,②④;利用“两组对角相等的四边形是平行四边形”(可利用四边形的内角和定理证明同旁内角互补,转化为两组对边分别平行)的条件有:⑤⑥,①⑤,①⑥,②⑤,②⑥.【来源:21cnj*y.co*m】
3、D
【解析】由题意可得(a-b)2+(c-d)2=0,
∴a=b,c=d,∴四边形ABCD为平行四边形.
二、填空题
1、4.
【解析】在 ABCD中,OB=OD ( http: / / www.21cnjy.com ),OA=OC, 又∵点E是AD的中点,∴OE是△ACD的中位线,∴OE=CD.∵△BCD的周长为8 cm,即BC+CD+BD=8 cm.又∵DE=AD=BC,∴△DEO的周长=DE+OE+OD=BC+CD+BD=(BC+CD+BD)=×8=4(cm).
答案:4
2、25°
【解析】
两个平行四边形的周长相等,且有公共边CD,则 ( http: / / www.21cnjy.com )有AD=DE,即△ADE为等腰三角形,∠ADE=∠BCF=60°+70°=130°,∴∠DAE=25°.21教育网
3、 20.
【解析】
在 ABCD中,BC=AD=6,∵BE=2,
∴CE=4.∵AD∥BC,∴∠ADE=∠CED.
∵DE平分∠ADC,∴∠ADE=∠CDE.
∴∠CED=∠CDE,
∴CD=CE=4.∴ ABCD的周长是(6+4)×2=20.
三、解答题
1、证明:连接BD交AC于O点
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
又∵AE=CF
∴OE=OF
∴四边形BEDF是平行四边形
∴∠EBF=∠EDF
2、【解】 ∵E,F分别是AD,BC的中点,
∴AE=DE=AD,BF=CF=BC.
又∵四边形ABCD是平行四边形,
∴AD平行且等于BC.∴AE平行且等于FC,DE平行且等于BF,
∴四边形AECF和四边形BFDE都是平行四边形,
∴AF∥EC,BE∥DF,即FG∥EH,EG∥FH,
∴四边形EGFH是平行四边形.
3、【解】
证明:∵四边形ABCD是平行四边形,∴OD=OB,OA=OC
∴∠DFO=∠BEO, ∠FDO=∠EBO
∴△FDO≌△EBO
∴OF=OE
∴四边形AECF是平行四边形
4、(1)∵△ABE是等边三角形,EF⊥AB,
∴∠AEF=∠AEB=30°,AE=AB,∠EFA=90°.
又∵∠ACB=90°,∠BAC=30°,
∴∠EFA=∠ACB,∠AEF=∠BAC.
∴△ACB≌△EFA.
∴AC=EF.
(2)证明:∵△ACD是等边三角形,
∴AC=AD,∠DAC=60°.
由(1)的结论得AC=EF,∴AD=EF.
又∵∠BAC=30°,∴∠FAD=∠BAC+∠DAC=90°.
又∵∠EFA=90°,∴EF∥AD.
又∵EF=AD,
∴四边形ADFE是平行四边形.
5、证明:□ABCD中,AD∥BC,AD=BC,∠ADC=∠ABC.
∵AD∥BC,∴∠G=∠H.
∵∠ADC=∠ABC,∴∠GDC=∠HBA.
在△GDE和△HBF中,∠G=∠H.∠GDC=∠HBA,DE=BF.
∴△GDE≌△HBF,∴GD=BH.∵AD=BC,∴AC=GH.
∵平行四边形ABCD中,AD∥BC,∴∠DAC=∠BCA.
在△AGO和△CHO中,∠G=∠H,∠DAC=∠BCA,AG=CH.
∴△AGO≌△CHO,∴OG=OH,OA=OC.∴AC、GH互相平分.
6、 如解图,连结AC,延长AB和DC交于点F,过点B作BM⊥CF于点M.
(第14题解)
∵∠ABC=∠DCB=120°,
∴∠FBC=∠FCB=60°,
∴△CBF是等边三角形,
∴∠F=60°,CF=BF=BC=4.
∵BM⊥CF,
∴CM=FM=2.
∴由勾股定理,得BM=2.
∵∠EAB=120°,∠F=60°,
∴∠EAB+∠F=180°,
∴AE∥DF.
同理,DE∥AF.
∴四边形EAFD是平行四边形.
∴DE=AF=AB+BF=8,
AE=DF=CD+CF=12.
∴五边形的周长=DE+DC+BC+AB+AE=36.
∵∠ABC=120°,BC=AB=4,
∴∠BCA=∠BAC=30°,
∴∠ACF=180°-(120°-30°)=90°.
在Rt△ACF中,由勾股定理,得AC=4,
∴五边形的面积=S DEAF-S△CBF=AE·AC-CF·BM=12×4-×4×2=44.
答:五边形的周长是36,面积是44.
D
A
E
F
B
C
C
A
B
D
E
F
O
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
