3.3 方差和标准差 同步练习

方差和标准差
班级：___________姓名：___________得分：__________
选择题
1、某校A、B两队10名参加篮球比赛的队员的身高（单位：cm）如下表所示：
队员
队
1号
2号
3号
4号
5号
A队
176
175
174
171
174
B队
170
173
171
174
182
设两队队员身高的平均数分别为，身高的方差分别为SA2，SB2，则正确的选项是（　　）
A、 B、
C、 D、
2、在社会实践活动中，某同学对甲、乙、丙、丁四个城市一至五月份的白菜价格进行调查．四个城市5个月白菜的平均值均为3.50元，方差分别为S甲2＝18.3，S乙2＝17.4，S丙2＝20.1，S丁2＝12.5．一至五月份白菜价格最稳定的城市是（　　）21教育网
A、甲 B、乙 C、丙 D、丁
3、一次数学测试，某小组五名同学的成绩如下表所示（有两个数据被遮盖）．
组员
甲
乙
丙
丁
戊
方差
平均成绩
得分
81
79
■
80
82
■
80
那么被遮盖的两个数据依次是（　　）
A．80，2 B．80， C．78，2 D．78，
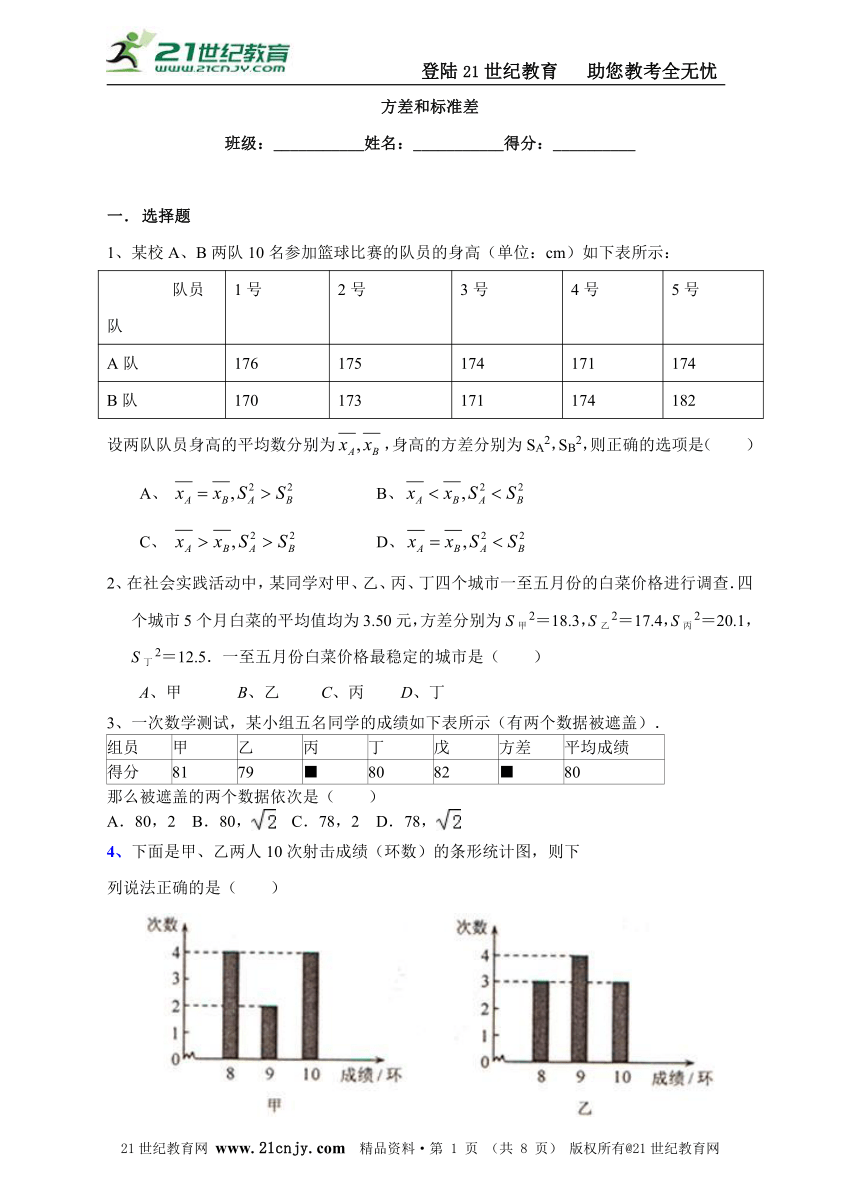
4、下面是甲、乙两人10次射击成绩（环数）的条形统计图，则下
列说法正确的是（　　）
A、甲比乙的成绩稳定 B、乙比甲的成绩稳定
C、甲、乙两人的成绩一样稳定 D、无法确定谁的成绩更稳定
5．某学习小组5位同学参加初中毕业生实验操作考试（满分20分）的平均成绩是16分．其中三位男生的方差为6（分2），两位女生的成绩分别为17分，15分．则这个学习小组5位同学考试分数的标准差为（ ）21cnjy.com
A． B．2 C． D．6
二、填空题
1、如果样本方差：S2=[+++…+]，那么这个样本的平均数为　 　．
2、对甲、乙、丙三名射击手进行20次测试，平均成绩都是8.5环，方差分别是0.4，3.2，1.6，在这三名射击手中成绩比较稳定的是　 　．www-2-1-cnjy-com
3、甲、乙两台机床生产同一种零件，并且每天产量相等，在6天中每天生产零件中的次品数依次是：甲：3、0、0、2、0、1；乙：1、0、2、1、0、2．则甲、乙两台机床中性能较稳定的是　 　．2-1-c-n-j-y
4、已知一组数据5，8，10，x，9的众数是8，那么这组数据的方差是　 　．
三、解答题
1、省射击队为从甲、乙两名运动员中选拔一人参加全国比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：21*cnjy*com
第一次
第二次
第三次
第四次
第五次
第六次
甲
10
8
9
8
10
9
乙
10
7
10
10
9
8
（1）根据表格中的数据，计算出甲的平均成绩是　 　环，乙的平均成绩是　 　环；
（2）分别计算甲、乙六次测试成绩的方差；
（3）根据（1）、（2）计算的结果，你认为推荐谁参加全国比赛更合适，请说明理由．
（计算方差的公式：s2＝［］
2、某班实行小组量化考核制，为了了解同学们的学习情况，王老师对甲、乙两个小组连续六周的综合评价得分进行了统计，并将得到的数据制成如下的统计表：
综合评价得分统计表
组别 周次
一
二
三
四
五
六
甲组
12
15
16
14
14
13
乙组
9
14
10
17
16
18
（1）请根据上表中的数据完成下表（注：方差的计算结果精确到0.1）
（2）根据综合评价得分统计表中的数据，请在下图中画出乙组综合评价得分的折线统计图．
（3）根据折线统计图中的信息，请你分别对甲、乙两个小组连续六周的学习情况作出简要评价．
3．为选派一名学生参加全市实践活动技能竞赛，A、B两位同学在学校实习基地现场进行加工直径为20mm的零件的测试，他俩各加工的10个零件的相关数据依次如下图表所示（单位：mm） 21世纪教育网版权所有
平均数
方差
完全符合
要求个数
A
20
0.026
2
B
20
SB2
5
根据测试得到的有关数据，试解答下列问题：
（1）考虑平均数与完全符合要求的个数，你认为　B　的成绩好些；
（2）计算出SB2的大小，考虑平均数与方差，说明谁的成绩好些；（3）考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况，你认为派谁去参赛较合适？说明你的理由．www.21-cn-jy.com
4、甲、乙两位同学本学年每个单元的测验成绩如下（单位：分）：
甲：98，100，100，90，96，91，89，99，100，100，93
乙：98，99，96，94，95，92，92，98，96，99，97
（1）他们的平均成绩分别是多少？
（2）甲、乙的11次单元测验成绩的标准差分别是多少？
（3）这两位同学的成绩各有什么特点？
（4）现要从中选出一人参加“希望杯”竞赛，历届比赛成绩表明，平时成绩达到98分以上才可能进入决赛，你认为应选谁参加这项竞赛，为什么？2·1·c·n·j·y

参考答案
选择题、
1.D
【解析】
解：∵=（176+175+174+171+174）=174cm，
=（170+173+171+174+182）=174cm．
SA2= [（176﹣174）2+（173﹣174）2+（171﹣174）2+（174﹣174）2+（182﹣174）2]=3.6cm2；
SB2=[（170﹣174）2+（175﹣174）2+（174﹣174）2+（171﹣174）2+（174﹣174）2]=5.2cm2；
∴．
故选D．
2． D
【解析】解：因为丁城市的方差最小，所以丁最稳定．
故选D．
C
【解析】解：根据题意得：
80×5﹣（81+79+80+82）=78，
方差=[（81﹣80）2+（79﹣80）2+（78﹣80）2+（80﹣80）2+（82﹣80）2]=2．
故选C．
B
【解析】解：通过观察条形统计图可知：乙的成绩更整齐，也相对更稳定，
故选B．
B
【解析】解：三位男生的方差为6（分2），
设这三个学生的成绩分别为A，B，C，
则5位学生的平均成绩为：（A+B+C+17+15）=16，
所以，A+B+C=80﹣15﹣17=48分，
则这三个学生的平均成绩的也为16，
这三个学生的方差S3=[（A﹣16）2+（B﹣16）2+（C﹣16）2]=6
∴[（A﹣16）2+（B﹣16）2+（C﹣16）2]=6×3=18
这5个学生的方差S5=[（A﹣16）2+（B﹣16）2+（C﹣16）2+（17﹣16）2+（15﹣16）2]=（18+1+1）=4，21·cn·jy·com
而标准差是方差的算术平方根，所以标准差为2．
故选B．
二、填空题
1、5
【解析】解：∵在公式S2=[（x1﹣）2+（x2﹣）2+…+（xn﹣）2]平均数是，
∴在S2=[（x1﹣5）2+（x2﹣5）2+（x3﹣5）2+…+（x50﹣5）2]中，
这个样本的平均数为5．
故答案为：5．
2、甲
【解析】解：根据方差的定义，方差越小数据越稳定，因为S甲2=0.4，S乙2=3.2，S丙2=1.6，方差最小的为甲，所以本题中成绩比较稳定的是甲．【来源：21·世纪·教育·网】
故填答案为甲．
3、乙
【解析】解：甲的平均数=（3+0+0+2+0+1）=1，
乙的平均数=（1+0+2+1+0+2）=1，
∴S2甲= [（3﹣1）2+3×（0﹣1）2+（2﹣1）2+（1﹣1）2]=
S2乙= [（2×（1﹣1）2+2×（0﹣1）2+2×（2﹣1）2]=
∴S2甲＞S2乙，
∴乙台机床性能较稳定．
故答案为乙．
4、2.8
【解析】解：∵一组数据5，8，10，x，9的众数是8，
∴x是8，
∴这组数据的平均数是（5+8+10+8+9）÷5=8，
∴这组数据的方差是：
[（5﹣8）2+（8﹣8）2+（10﹣8）2+（8﹣8）2+（9﹣8）2]=2.8．
故答案为：2.8．
三、解答题
1、解：（1）甲：（10+8+9+8+10+9）÷6=9，
乙：（10+7+10+10+9+8）÷6=9；
（2）s2甲＝
＝＝；
s2乙＝
＝＝．
（3）推荐甲参加全国比赛更合适，理由如下：两人的平均成绩相等，说明实力相当；但甲的六次测试成绩的方差比乙小，说明甲发挥较为稳定，故推荐甲参加比赛更合适．
2、（1）
平均数
中位数
方差
甲组
14
14
1.7
乙组
14
15
11.7
（2）
（3）从折线图可看出：甲组成绩相对稳定，但进步不大，且略有下降趋势；乙组成绩不够稳定，但进步较快，呈上升趋势．21·世纪*教育网
3、解：（1）根据表中数据可看出，B的完全符合要求的件数多，B的成绩好些．
（2）∵sB2=[4（20﹣20）2+3（19.9﹣20）2+2（20.1﹣20）2+（20.2﹣20）2]=0.008，
且sA2=0.026，
∴sA2＞sB2，即在平均数相同的情况下，B的波动性小，
∴B的成绩好些；
（3）从图中折线走势可知，尽管A的成绩前面起伏大，但后来逐渐稳定，误差小，预测A的潜力大，而B比较稳定，潜力小，所以不让B参加，而派A参加，即可选派A去参赛．
4、解：（1）甲＝×（98＋100＋100＋90＋96＋91＋89＋99＋100＋100＋93）＝96
乙＝×（98＋99＋96＋94＋95＋92＋92＋98＋96＋99＋97）＝96
（2）s2甲＝×［（98－96）2＋（100－96）2＋…＋（93－96）2］＝17.82
∴s甲＝4.221
s2乙＝×［（98－96）2＋（99－96）2＋…＋（97－96）2］＝5.817
∴s乙＝2.412
（3）乙较甲稳定，甲虽然状态不稳定，但发挥好时成绩比乙优秀．
（4）选甲去，甲比乙更有可能达到98分．