5.2.2 菱形的判定 同步练习

21世纪教育网 –中小学教育资源及组卷应用平台
5.2菱形（2）
一．选择题
1．如图，已知四边形ABCD是平行四边形，要使它成为菱形，那么需要添加的条件可以是（　　）
( http: / / www.21cnjy.com )
A．AC⊥BD B．AB=AC C．∠ABC=90° D．AC=BD
2．下列命题是真命题的是（　　）
A．有一个角是直角的四边形是矩形
B．有一组邻边相等的四边形是菱形
C．有三个角是直角的四边形是矩形
D．有三条边相等的四边形是菱形
3．如图，在由六个全等的正三角形拼成的图中，菱形的个数为（　　）
( http: / / www.21cnjy.com )
A．3 B．4 C．5 D．6
4．已知四边形ABCD是平行四边形，再从 ( http: / / www.21cnjy.com )①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD四个条件中，选一个作为补充条件后，使得四边形ABCD是菱形，现在下列四种选法，其中都正确的是（　　）21cnjy.com
A．①或② B．②或③ C．③或④ D．①或④
5．如图，是一张平行四边形纸片ABCD，要求利用所学知识将它变成一个菱形，甲、乙两位同学的作法分别如下：【来源：21·世纪·教育·网】
( http: / / www.21cnjy.com )
对于甲、乙两人的作法，可判断（　　）
A．甲正确，乙错误 B．甲错误，乙正确
C．甲、乙均正确 D．甲、乙均错误
6．四边形的四边长顺次为a、b、c、d，且a2+b2+c2+d2=ab+bc+cd+ad，则此四边形一定是（　　）
A．平行四边形 B．矩形 C．菱形 D．正方形
二．填空题
1．如图，在平行四边形ABCD中，AD=5，AB=3，AE平分∠BAD交BC边于点E，则EC的长为　 　．2·1·c·n·j·y
( http: / / www.21cnjy.com )
2．如图，矩形ABCD中，AB=4，BC= ( http: / / www.21cnjy.com )8，点E是边AD上一动点，点O是对角线BD的中点，连接EO并延长交于点F，当AE的长为　 　时，四边形BFDE是菱形．
( http: / / www.21cnjy.com )
3．在四边形ABCD中，给出四个条件：①A ( http: / / www.21cnjy.com )B=CD，②AD∥BC，③AC⊥BD，④AC平分∠BAD，由其中三个条件推出四边形ABCD是菱形，你认为这三个条件是　 　．（写四个条件的不给分，只填序号）21·世纪*教育网
4．如图，在给定的一张平行 ( http: / / www.21cnjy.com )四边形纸片上作一个菱形．小米的作法是：连接AC，作AC的垂直平分线MN分别交AD，AC，BC于M，O，N，连接AN，CM，则四边形ANCM是菱形．则小米的依据是　 　．www-2-1-cnjy-com
( http: / / www.21cnjy.com )
三．解答题
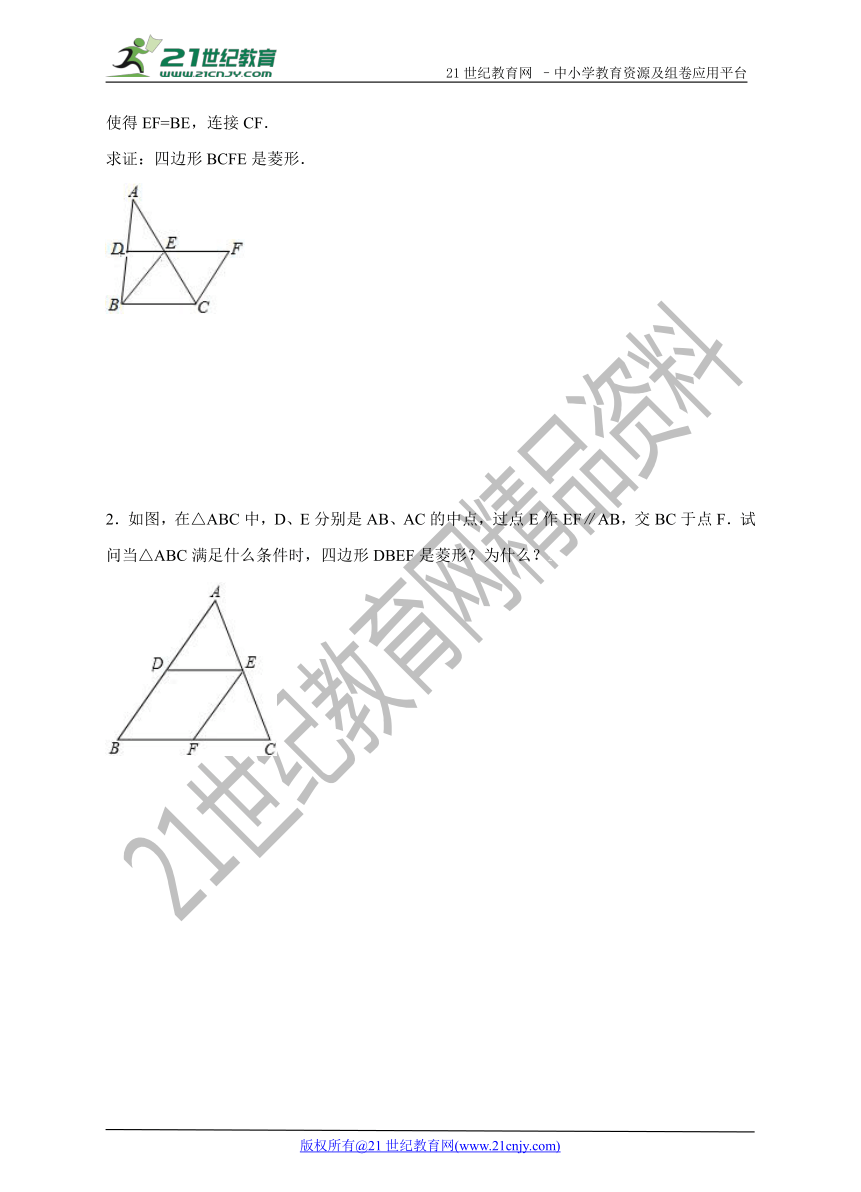
1．已知：如图，在△ABC中，D、E分别是AB、AC的中点，BE=2DE，延长DE到点F，使得EF=BE，连接CF．2-1-c-n-j-y
求证：四边形BCFE是菱形．
( http: / / www.21cnjy.com )
2．如图，在△ABC中，D、E分别是A ( http: / / www.21cnjy.com )B、AC的中点，过点E作EF∥AB，交BC于点F．试问当△ABC满足什么条件时，四边形DBEF是菱形？为什么？21*cnjy*com
( http: / / www.21cnjy.com )
3．如图，四边形ABCD中，AB∥CD，AC平分∠BAD，CE∥AD交AB于E．
（1）求证：四边形AECD是菱形；
（2）如果点E是AB的中点，AC=4，EC=2.5，求四边形ABCD的面积．
( http: / / www.21cnjy.com )
参考答案
一．选择题
1．A
【解析】A、∵四边形ABCD是平行四边形，AC⊥BD，
∴平行四边形ABCD是菱形，故本选项正确；
B、∵四边形ABCD是平行四边形，AB=AC≠BC，
∴平行四边形ABCD不是，故本选项错误；
C、∵四边形ABCD是平行四边形，∠ABC=90°，
∴四边形ABCD是矩形，
不能推出，平行四边形ABCD是菱形，故本选项错误；
D、∵四边形ABCD是平行四边形，AC=BD
∴四边形ABCD是矩形，不是菱形．
故选：A．
2．C
【解析】A、有一个角是直角的平行四边形是矩形，故选项错误；
B、四条边都相等的四边形是菱形，故选项错误；
C、有三个角是直角的四边形是矩形，故选项正确；
D、四条边都相等的四边形是菱形，故选项错误．
故选C．
3．D
【解析】如图，
( http: / / www.21cnjy.com )
由题意可知，EF∥AD∥BC，ED ( http: / / www.21cnjy.com )∥FC∥AB，CD∥BE∥AF，有ED=EF=AF=AB=BC=CD=GE=GF=GA=GB=GC=GD，21教育网
∴四边形EDGF，EDCG，FGBA，GCBA，EGAF，CDGB是平行四边形，
∵AB=BC=CD=DE=EF=AF，
∴平行四边形EDGF，EDCG，FGBA，GCBA，EGAF，CDGB都是菱形，共6个．
故选D．
4．D
【解析】①∵四边形ABCD是平行四边形，AB=BC，
∴四边形ABCD是菱形，故本选项正确；
②∵四边形ABCD是平行四边形，∠ABC=90°，
∴四边形ABCD是矩形，
不能推出，平行四边形ABCD是菱形，故本选项错误；
③∵四边形ABCD是平行四边形，AC=BD，
∴平行四边形ABCD是矩形，故本选项错误；
④∵四边形ABCD是平行四边形，AC⊥BD，
∴平行四边形ABCD是菱形，故本选项正确，
故选：D．
5．C
【解析】首先证明△AOE≌△COF ( http: / / www.21cnjy.com )（ASA），可得AE=CF，再根据一组对边平行且相等的四边形是平行四边形可判定判定四边形AECF是平行四边形，再由AC⊥EF，可根据对角线互相垂直的四边形是菱形判定出AECF是菱形；四边形ABCD是平行四边形，可根据角平分线的定义和平行线的定义，求得AB=AF，所以四边形ABEF是菱形．21世纪教育网版权所有
6．C
【解析】整理配方式子a2+b2+c2+d2=ab+bc+cd+ad，
2（a2+b2+c2+d2）=2（ab+bc+cd+ad），
∴（a﹣b）2+（b﹣c）2+（c﹣d）2+（a﹣d）2=0，
由非负数的性质可知：（a﹣b）=0，（b﹣c）=0，（c﹣d）=0，（a﹣d）=0，
∴a=b=c=d，
∴四边形一定是菱形，
故选C．
二．填空题
1．2
【解析】过点E作EF∥AB，交AD于F
∵在平行四边形ABCD，EF∥AB
∴AB=EF，AF=BE
∵∠FAE=∠BAE
∴△AFE≌△ABE
∴AB=BE=EF=AF
∴ABEF为菱形
∴EC=AD﹣AB=2．
故答案为：2．
( http: / / www.21cnjy.com )
2．3
【解析】∵四边形ABCD是矩形，
∴AD∥BC，OB=OD，
∵∠EDO=∠FBO，∠OED=∠OFB，
∴△OED≌△OFB，
∴DE=BF，
又∵ED∥BF，
∴四边形BEDF是平行四边形，
当平行四边形BFDE是菱形时，ED=BE，
设AE=x，
则BE=DE=8﹣x，
在Rt△AEB中，
x2+42=（8﹣x）2，解得：x=3
故当AE=3时， BEDF是菱形，
故答案为：3．
3．①③④或②③④．．
【解析】菱形的判定方法有三种：①定义：一组邻边相等的平行四边形是菱形；②四边相等；③对角线互相垂直平分的四边形是菱形．据此判断即可．21·cn·jy·com
4．对角线互相垂直的平行四边形是菱形．
【解析】先根据MN垂直平分AC，推导出△AO ( http: / / www.21cnjy.com )M≌△CON，进而的而出AM=CN，再根据AM∥CN，判定四边形AMCN是平行四边形，最后根据MN⊥AC，得出四边形AMCN是菱形．www.21-cn-jy.com
三．解答题
1．答案见解析
【解析】∵BE=2DE，EF=BE，
∴EF=2DE．
∵D、E分别是AB、AC的中点，
∴BC=2DE且DE∥BC．
∴EF=BC．
又EF∥BC，
∴四边形BCFE是平行四边形．
又EF=BE，
∴四边形BCFE是菱形．
2．答案见解析
【解析】当AB=BC时，四边形DBFE是菱形．理由如下：
∵D、E分别是AB、AC的中点，
∴DE是△ABC的中位线，
∴DE∥BC，
又∵EF∥AB，
∴四边形DBFE是平行四边形；
∵D是AB的中点，
∴BD=AB，
∵DE是△ABC的中位线，
∴DE=BC，
∵AB=BC，
∴BD=DE，
∴四边形DBFE是菱形．
3．答案见解析
【解析】（1）证明：∵AB∥CD，CE∥AD，
∴四边形AECD是平行四边形，…（1分）；
∵AC平分∠BAD，
∴∠EAC=∠DAC，
∵AB∥CD，
∴∠EAC=∠ACD，
∴∠DAC=∠ACD，
∴AD=CD，
∴四边形AECD是菱形．
（2）解：∵四边形AECD是菱形，
∴AE=CE，
∴∠EAC=∠ACE，
∵点E是AB的中点，
∴AE=BE，
∴∠B=∠ECB，
∴∠ACE+∠ECB=90°，即∠ACB=90°；
∵点E是AB的中点，EC=2.5，
∴AB=2EC=5，
∴BC=3．
∴S△ABC=BC AC=6．
∵点E是AB的中点，四边形AECD是菱形，
∴S△AEC=S△EBC=S△ACD=3．
∴四边形ABCD的面积=S△AEC+S△EBC+S△ACD=9．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)