5.3.1 正方形的性质 同步练习

21世纪教育网 –中小学教育资源及组卷应用平台
5.3.1正方形的性质
班级：___________姓名：___________得分：__________
1、选择题
1、下列说法不正确的是(　　)
A．一组邻边相等的矩形是正方形
B．对角线相等的菱形是正方形
C．对角线互相垂直的矩形是正方形
D．有一个角是直角的平行四边形是正方形
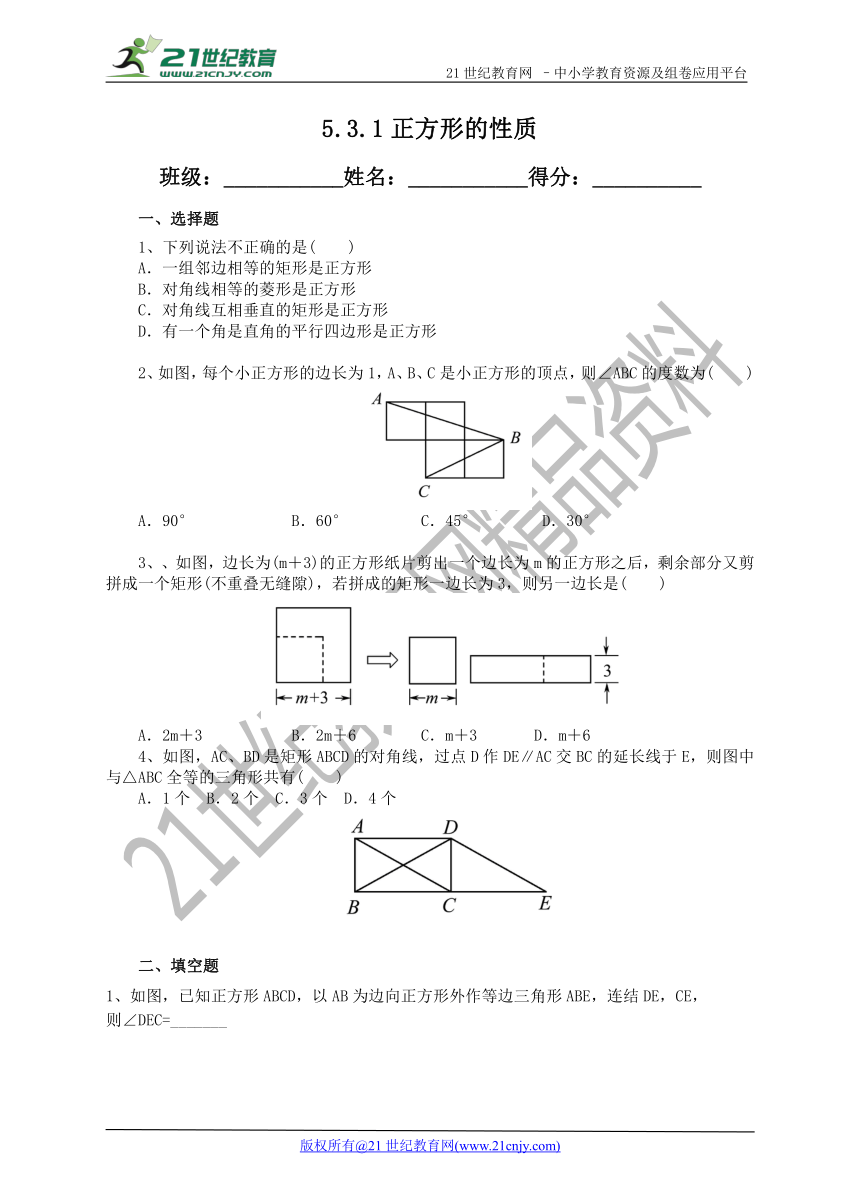
2、如图，每个小正方形的边长为1，A、B、C是小正方形的顶点，则∠ABC的度数为(　　)
A．90° B．60° C．45° D．30°
3、、如图，边长为(m＋3)的正方形纸片 ( http: / / www.21cnjy.com )剪出一个边长为m的正方形之后，剩余部分又剪拼成一个矩形(不重叠无缝隙)，若拼成的矩形一边长为3，则另一边长是(　　)
A．2m＋3 B．2m＋6 C．m＋3 D．m＋6
4、如图，AC、BD是矩形ABCD的对角线，过点D作DE∥AC交BC的延长线于E，则图中与△ABC全等的三角形共有(　　)21世纪教育网版权所有
A．1个 B．2个 C．3个 D．4个
2、填空题
1、如图，已知正方形ABCD，以AB为边向正方形外作等边三角形ABE，连结DE，CE，
则∠DEC=_______
( http: / / www.21cnjy.com )
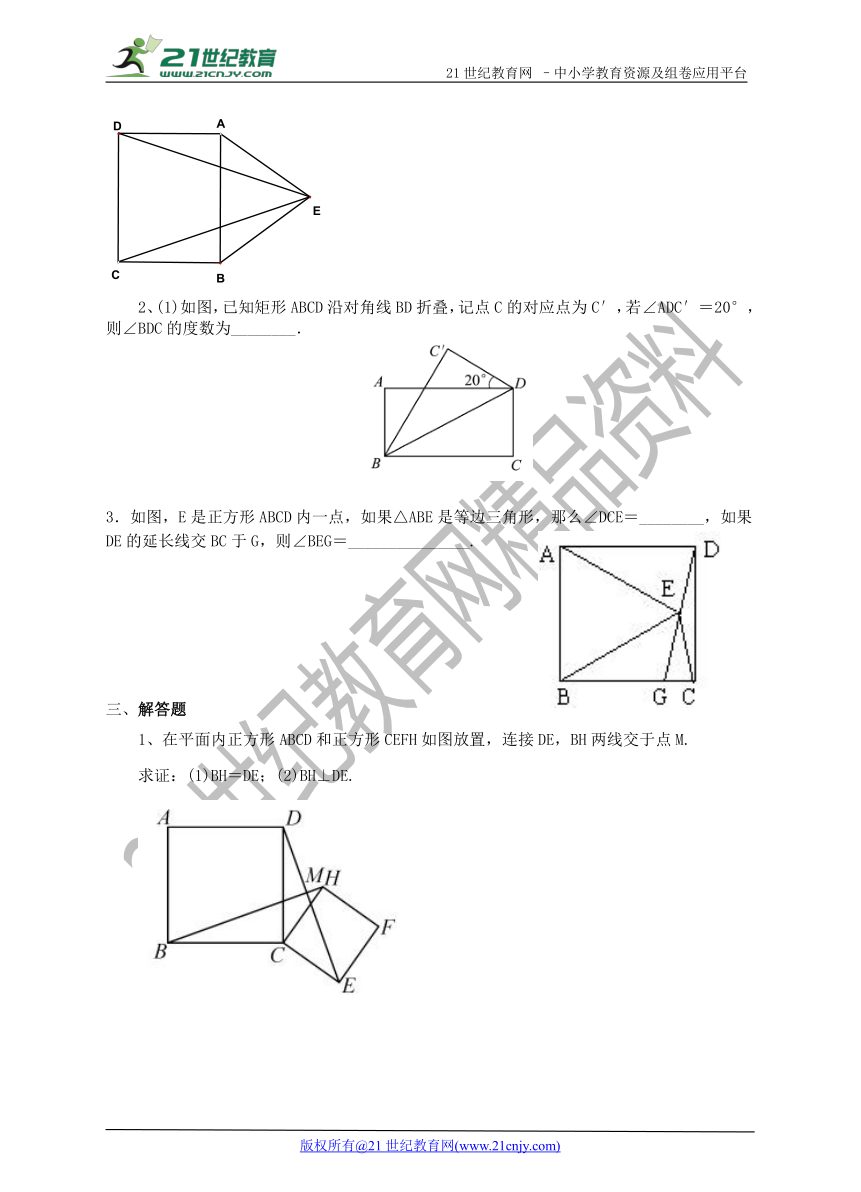
2、(1)如图，已知矩形ABCD沿对角线BD折叠，记点C的对应点为C′，若∠ADC′＝20°，则∠BDC的度数为________．21cnjy.com
3．如图，E是正方形ABCD内一点，如果△ABE是等边三角形，那么∠DCE＝________，如果DE的延长线交BC于G，则∠BEG＝_______________. www.21-cn-jy.com
三、解答题
1、在平面内正方形ABCD和正方形CEFH如图放置，连接DE，BH两线交于点M.
求证：(1)BH＝DE；(2)BH⊥DE.
( http: / / www.21cnjy.com )
2、在△ABC中,AB=AC,D是BC的中点,DE⊥AB, DF⊥AC,垂足分别是E,F.
⑴试说明:DE=DF
⑵只添加一个条件,使四边形EDFA是正方形.请你至少写出两种不同的添加方法.(不另外添加辅助线,无需证明。 版权所有21·cn·jy·com
3、如图，四边形ABCD是正方形，G是B ( http: / / www.21cnjy.com )C上任意一点(点G与B、C不重合)，AE⊥DG于E，CF∥AE交DG于F．求证：AE=FC+EF．【来源：21·世纪·教育·网】
( http: / / www.21cnjy.com )
4、已知：如图，矩形ABCD的外角平分线围成四边形EFGH．
求证：四边形EFGH是正方形．
5.AC为正方形ABCD的对角线，E为AC上一点，且AB=AE,EF垂直AC交BC 于F,求证EC=EF=FB21教育网
( http: / / www.21cnjy.com )
6、如图，在正方形ABCD中，E为CD上一点，F为BC边延长线上一点，且CE=CF.BE与DF之间有怎样的关系？请说明理由.21·世纪*教育网
( http: / / www.21cnjy.com )
参考答案
一、选择题
1、D
【解析】
当一个四边形既是菱形又是矩形时，它就是正方形
2、C
【解析】 连结AC，可证得△ACB是等腰直角三角形，∴∠ABC的度数为45°.
3、A
【解析】
设另一边长为a，由面积法可得：(m＋3)2＝m2＋3·a，∴a＝2m＋3.
4．D
【解析】根据矩形的性质，△CDA、△BAD ( http: / / www.21cnjy.com )、△DCB与△ABC全等，因为DE∥AC，所以∠CDE＝∠DCA，因为CD＝DC，∠ADC＝∠ECD，所以△ADC≌△ECD，所以与△ABC全等的三角形有4个，故选择D.2·1·c·n·j·y
二、填空题
1、30°．
【解析】△ABE为等边三角 ( http: / / www.21cnjy.com )形∠BAE=60°， ∠DAE=150°， △ABE为等腰三角形， ∠AED=15°同理∠BEC=15°所以∠DEC=30°2-1-c-n-j-y
答案：30°
2、55°
【解析】
本题考查矩形的性质和折叠全等的问题，设∠BDC＝x°，则∠ADB＝(90－x)°，∴x＝90－x＋20，∴x＝55°.21*cnjy*com
3、∠EDC=150 ∠BEG＝450
【解析】∵△ABE是等边三角形，
∴∠ABE=∠AEB=60°，BE=AB，
∵四边形ABCD是正方形，
∴AB=BC，∠ABC=∠BCD=90°，
∴BE=BC，∠CBE=90-60°=30°，
∴∠BCE=∠BEC=（180°-30°）=75°，
∴∠DCE=∠BCD-∠BCE=90°-75°=15°；
由对称性可得∠AED=∠BEC=75°，
∴∠BEG=180°-∠AED-∠AEB=180°-75°-60°=45°．
故答案为：15°；45°．
三、解答题
1、证明：(1)在正方形ABCD与正方形CEFH中，
BC＝CD，CE＝CH，∠BCD＝∠ECH＝90°，∴∠BCD＋∠DCH＝∠ECH＋∠DCH，
即∠BCH＝∠DCE，
∴△BCH≌△DCE，
∴BH＝DE
(2)由(1)得，∠CBH＝∠CDE，
∴∠DMB＝∠BCD＝90°，
∴BH⊥DE　
2、证明：⑴连结AD，∵AB＝AC，D为BC的中点
　　∴AD为∠BAC的平分线.
　　∵DE⊥AB，DF⊥AC，∴DE＝DF.
　　⑵∠BAC＝90°， DE⊥DF.
3、解：∵四边形ABCD是正方形，∴AD=DC，∠ADC=90°，
又∵AE⊥DG，CF∥AE，∴∠AED=∠DFC=90°，
∴∠EAD+∠ADE=∠FDC+∠ADE=90°，∴∠EAD=∠FDC，
∴△AED≌△DFC(AAS)，∴AE=DF，ED=FC，
∵DF=DE+EF，∴AE=FC+EF．
4、解：由△EAB与△GCD、△FBC与△HAD是两对全等的等腰直角三角形，
推得EA+AH=EB+BF=GC+FC=GD+DH，即EH=EF=GF=GH．∴四边形EFGH是菱形．
又∵∠E=90°，∴四边形EFGH是正方形．
5、证明：在Rt△AEF和Rt△ABF中，
AE＝AB
AF＝AF，
∴Rt△AEF≌Rt△ABF（HL），
∴FE=FB．∵正方形ABCD，
∴∠ACB=45°，
在Rt△CEF中，∵∠ACB=45°，
∴∠CFE=45°，∴∠ACB=∠CFE，
∴EC=EF，
∴FB=EC．
6、解：BE=DF,且BE⊥DF.理由如下：
（1） ∵四边形ABCD是正方形.
∴BC=DC,∠BCE=90°（正方形的四条边都相等，四个角都是直角）
∴∠DCF=180°-∠BCE=180°-90°=90°
∴∠BCE=∠DCF
又∵CE=CF
∴△BCE≌△DCF
∴BE=DF.
(2)延长BE交DE于点M
∵△BCE≌△DCF
∴∠CBE=∠CDF
∵∠DCF=90°
∴∠CDF+∠F=90°
∴∠CBE+∠F=90°
∴∠BMF=90°
∴BE⊥DF
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)